Главная | Обратная связь | Поможем написать вашу работу!

Представление данных в табличной форме

Расписание движения поездов, сведения о сотрудниках предприятия, статистические данные о демографической ситуации в стране — данные подобного рода чаще всего представляются в табличной форме. Процесс обучения в школе тоже часто отображается в табличных моделях. Это и расписание уроков, и классный журнал, и аттестат о среднем образовании.

Пример. Посмотрите на страничку классного журнала.

Таблица 1. Страница классного журнала (фрагмент)

ИНФОРМАТИКА
	ФИО	Апрель				Май
		5	12	19	26	3	10
1	Альтов Г.	4		5		4
2	Беседова Ф.			4	3
3	Веселов А.		5	4		5	5

Информационной моделью какого объекта (процесса) является эта таблица? Какие сведения можно из неё извлечь? О чём, например, говорит цифра «5» в правой нижней ячейке таблицы? В таблице отражаются результаты контроля знаний учащихся и успешность процесса обучения. Цифра «5» в правой нижней ячейке имеет отношение к ученику по фамилии Веселов, предмету информатике, месяцу маю, 10 дню этого месяца и году, который указан на обложке журнала. Таким образом, оценка в классном журнале устанавливает отношение между тремя объектами: учеником, учебным предметом, датой. Анализ таблицы позволит узнать успешность обучения каждого ученика, определить, сколько в классе отличников и неуспевающих, оценить сложность предложенной учащимся контрольной работы; поможет учителю выработать меры педагогического воздействия. Классный журнал можно рассматривать как формализованную, динамическую, вероятностную информационную модель «поведения» процесса обучения в данном классе.

Таблицы, в которых отражается одно свойство, характеризующее два или более объектов, называются таблицами типа «объект - объект». Причём объекты принадлежат, как правило, к разным классам (множествам). В примере таким свойством является успеваемость, объектами — конкретные ученики (принадлежат множеству учеников), учебный предмет (принадлежат множеству школьных дисциплин), даты (множество дат).

Есть таблицы другого вида, в которых отражаются несколько свойств объекта, а все объекты принадлежат к одному множеству. Такие таблицы называются таблицами вида «объект - свойство».

Пример

Таблица 2. Результаты медицинского наблюдения класса (фрагмент)


	ФИО ученика	Дата рождения	Рост, см	Вес, кг	Жизненная ёмкость лёгких, см³	Острота зрения
1	Альтов Г.	12.12.1988	165	62	3300	1
2	Беседова Ф.	01.03.1989	168	55	3200	0,9
3	Веселов А.	10.10.1988	172	59	3400	1

Данную таблицу можно рассматривать как информационную модель состояния физического развития учащихся класса. Объектами, информация о которых отражена в таблице, являются ученики, каждый из которых характеризуется конкретными значениями перечисленных в верхней строке таблицы свойств — параметров физического развития. Подумайте, для чего необходимо составление таких таблиц и какую информацию можно получить, анализируя приведённые в них данные. Комбинирование нескольких таблиц вида «объект - объект» и «объект - свойство» в одной таблице позволяет построить таблицы более сложного вида.

Существуют определенные правила оформления таблиц, в соответствии с которыми каждая таблица характеризуется:

• названием (а если таблиц несколько, то ещё и номером),

• количеством столбцов и их названиями (заголовками столбцов),

• количеством строк и их названиями (заголовками строк),

• содержимым ячеек, находящихся на пересечении строк и столбцов.

В соответствии с этим основными элементами таблицы являются:

• записи — строки таблицы, которые могут содержать данные разного типа, но относящиеся чаще всего к одному объекту;

• поля — столбцы таблицы, содержащие, как правило, данные одного типа;

• реквизиты — конкретные значения, находящиеся в ячейках таблицы на пересечении строк и столбцов. Иногда заголовки строк и столбцов могут оказаться многоуровневыми. В этом случае уровни заголовков столбцов называются ярусами, уровни заголовков строк — ступенями.

Пример

Таблица 3. Выпуск продукции на кондитерской фабрике (тонн)

Таблицы — удобная для анализа и обработки, наглядная и привычная форма представления информации. Поэтому большинство автоматизированных баз данных имеет табличный или реляционный (от англ. relation — отношение) тип. Этапы построения таблицы (приведения информации к табличной форме) разберём на следующем примере.

Пример

Переведём словесное описание характеристик нескольких регионов Российской Федерации, взятое из географического энциклопедического словаря, в табличную форму

Ростовская область - Пл. 100,8 т.км. Нас. 4290 т.ч. (1987; в Ростове-на-Дону 1004 т.ч.), гор. 72%. 42 адм. р-на, 22 города, 37 пгт (1987). Центр — Ростов-на-Дону. Ср. темп-ры января от -9 °С до -5 °С, июля 22-24 °С. Осадков 400-650 мм в год.

Московская область - Пл. 47 т.км. Нас. 6581 т.ч. (1987; с Москвой 15396 т.ч<); гор. 79% (с учетом нас. Москвы 91%). 39 адм. р-нов, 71 город, 109 пгт (1987). Центр — Москва. Ср. темп-ры января -10 "С, июля 17 °С. Осадков 450-650 мм в год.

Тамбовская область - Пл. 34,3 т.км. Нас. 1309 т.ч. (1987; в Тамбове 305?-ч.), гор. 56%. 23 адм. р-на, 8 городов, 13 пгт (1987). Центр — Тамбов. Ср. темп-ры января -11 °С, июля 20 °С. Осадков 500 мм в год.

Воронежская область - Пл. 52,4 т.км. Нас. 2459 т.ч. (1987; в Воронеже 87 т.ч.), гор. 60%. 32 адм. р-на, 14 городов, 23 пгт (1981/)- Центр — Воронеж. Ср. темп-ры января -9 °С, июля 20 °С. Осадков 500 мм в год.

Ленинградская область. Пл. 85,9 т.км. Нас. 1655 т.ч. (1987; с Санкт-Петербургом 6603 т.ч.), гор. 66%. 17 адм. р-нов, 26 городов, 41 пгт (1987). Центр — Санкт-Петербург. Ср. темп-ры января -7 °С, июля 15 °С. Осадков 850 мм в год.

Хабаровский край. Пл. 824,6 т.км. Нас. 1794 т.ч. (1987; в Хабаровске 591 т.ч.), гор. 79%. 22 адм. р-на, 9 городов, 43 пгт (1987)- Центр — Хабаровск. Ср. темп-ры января от -16 °С до ~40 °С, июля 11-21 °С. Осадков 500-900 мм в год.

Приведённые данные являются характеристиками регионов Российской Федерации» такими как: название, площадь, численность населения, административное деление, климатические условия. Эти характеристики сделаем названиями столбцов первого яруса. В свою очередь, численность населения раскрывается через такие параметры, как численность общего населения, численность населения центрального города, процент городского населения; «административное деление» включает в себя количество административных районов, количество городов и посёлков городского типа, название областного (краевого) центра; «климатические условия» описываются такими свойствами, как средние температуры января и июля и среднегодовое количество осадков. Перечисленные характеристики сделаем заголовками столбцов второго яруса. Всего столбцов в таблице будет 12. Кроме строк заголовка таблица будет содержать еще 6 строк для описания 6 субъектов федерации. В качестве заголовков строк лучше всего использовать названия регионов. Разместить записи можно в разном порядке, например, в порядке убывания общего количества жителей (первой будет Московская область, последней — Тамбовская) или занимаемой площади (первым будет Хабаровский край, последней Тамбовская область), но лучше использовать алфавитный порядок.

Таблица 4. Характеристики регионов Российской Федерации

Если объектов в таблице много, то размещать их можно, конечно, как угодно, но чтобы содержащиеся в ней данные было удобно анализировать и обрабатывать, располагать объекты лучше в некотором порядке, например, в алфавитном или по возрастанию даты и т. п.

Таблицы, рассмотренные в предыдущих примерах, было несложно построить и заполнить. Но иногда их разработка требует не только времени, но и определённых навыков и даже некоторого искусства.

Пример

Рассмотрим основные подходы к составлению школьного расписания. Заметим, что расписание занятий, предназначенное для учеников, будет отличаться от расписания тех же занятий, предназначенного для учителей. Так и должно быть, ведь цели моделирования различны. Как же строится таблица ученического расписания? Итак, задача — организовать учебный процесс так, чтобы выполнить учебный план и не нарушить законов о труде учителя; объектом моделирования является организация учебного процесса; субъектом моделирования — завуч; цель моделирования — определить для каждого класса порядок проведения занятий на каждый день недели и представить его в наглядной форме.

Существенные свойства:

• перечень классов в школе и список учителей;

• для каждого класса — перечень учебных дисциплин, фамилии ведущих их учителей и количество отводимых на них часов в неделю (таблица 5);

• для каждого учителя — перечень классов, название учебной дисциплины, количество часов в неделю (таблица 6);

• перечень учебных кабинетов и их назначение;

• количество и время проведения уроков и перемен в течение дня.

Таблица 5 (фрагмент)

Кл.	Предмет	Час.	Учитель
11а	Литература	4	Иванов В.В.
	Алгебра	6	Деева Г.П.
	Информатика	2	Летова А.Р.
	Физика	3	Петров С.А.

Таблица 6

Учитель	Предмет	Кл.	Час.
Летова А.Р.	Информ.	11а	2
	Информ.	116	2
	Логика	9к	1
	Информ.	9к	2

Заметим, что все эти списки и перечни надо предварительно составить, и они тоже являются информационными моделями табличной формы. Задайте вопрос завучу, как он составляет школьное расписание, и вы узнаете интересные методы формализации при построении моделей табличной формы. Вероятнее всего вы услышите, что составить расписание — дело очень сложное, потому что следует учесть много дополнительных факторов: пожелания учителей и учеников, требования гигиены умственного труда, санитарные требования и пр. Расписание в процессе составления неоднократно изменяется, уточняется, проверяется на непротиворечивость. Например, необходимо постоянно следить, чтобы у одного учителя не было занятий одновременно в двух классах, чтобы у разных классов не было занятий в одном и том же кабинете на одном и том же уроке, чтобы у учащихся не было «окон» и пр.

4. Представление информации в форме графа

Вы, вероятно, имеете представление о компьютерных сетях. Возможно, компьютеры в школьном кабинете информатики объединены в локальную сеть или вы работали в Интернете, или пользовались услугами электронной почты. Понятно, что сеть образуется только тогда, когда компьютеры каким-либо образом соединены между собой каналами передачи данных. Размещение абонентов сети (подключённых к ней компьютеров или других систем автоматической обработки данных) и способ их соединения друг с другом называется конфигурацией сети. Продемонстрировать различные типы конфигураций вычислительных сетей можно, например, с помощью таких информационных моделей, как графы. Граф — совокупность точек, соединённых между собой линиями. Точки называют вершинами графа. Они могут изображаться точками, кружочками, прямоугольниками и пр. Линии, соединяющие вершины, называются дугами (если задано направление от одной вершины к другой) или рёбрами (если направленность двусторонняя, то есть направления равноправны). Две вершины, соединенные ребром (дугой) называются смежными. Вершины и рёбра графа могут характеризоваться некоторыми числовыми величинами. Например, может быть известна длина ребра или «стоимость прохождения» по нему. Такие характеристики называют весом, а граф называется взвешенным.

Граф однозначно задан, если заданы множество его вершин, множество рёбер (дуг) и указано, какие вершины какими рёбрами (дугами) соединены и, возможно, указаны веса вершин и рёбер (дуг). Определение всех этих элементов и составляет суть формализации в этом случае.

Пример

На рис.3 представлены различные типы конфигураций локальных вычислительных сетей (ЛВС), являющиеся информационными моделями структур ЛВС, представленными в виде графов:

• шинная конфигурация, когда к незамкнутому каналу с некоторыми интервалами подключаются отдельные абоненты (К) информация от абонента-источника распространяется по каналу в обе стороны;

• кольцевая конфигурация, когда каждый абонент непосредственно связан с двумя соседними абонентами, а информация передаётся по замкнутому кольцу, чаще всего в одну сторону;

• звездообразная конфигурация, в центре которой находится центральный коммутатор (ЦК), который последовательно опрашивает абонентов и предоставляет им право на обмен данными;

• древовидная конфигурация образуется подсоединением нескольких простых каналов связи к одному магистральному;

• полносвязная конфигурация обеспечивает выбор наиболее быстрого маршрута связи между абонентами и удобна там, где управление оказывается достаточно сложным.

Рис.3 Различные типы конфигураций локальных вычислительных сетей

Наиболее наглядно граф задаётся рисунком. Однако не все детали рисунка одинаково важны. В частности, несущественны геометрические свойства рёбер (длина, кривизна и так далее), форма вершин (точка, кружок, квадрат, овал и пр.) и взаимное расположение вершин на плоскости. Так, на рис.4 представлены два изображения одного и того же графа. Все вершины и ребра часто задаётся в виде сопровождающей надписи на вершине или линии, но, введя условные обозначения, их можно задать формой или цветом вершины, толщиной, типом или цветом линии и т. п.

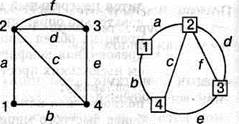
Рис. 4 Различные изображения одного и того же графа

Информационную модель в форме графа можно использовать для наглядного представления взаимосвязей, существующих между элементами объекта моделирования. Таким образом, граф — наиболее удобная форма для моделирования структуры объекта, хотя в такой форме можно моделировать и внешний вид, и поведение объекта.

Пример

На рис.5 представлены модели молекул бутана и изобутана, каждая из которых имеет формулу С4Н10, то есть состоит из 4 атомов углерода и 10 атомов водорода. Имея одну и ту же формулу, бутан и изобутан имеют различные химические свойства, так как способы соединения атомов (структура молекул) различны. Расположение атомов в молекуле при различных способах их соединения хорошо представимо графом.

Рис.5 Модели молекул бутана и изобутана

Заметим, что в химии для обозначения таких веществ часто используются и структурные формулы. Порядок соединения атомов изображается в структурной формуле чёрточками (связь между водородом и остальными атомами обычно не указывается). Подумайте сами, можно ли считать структурную формулу одной из разновидностей графа. В форме графа удобно отображать взаимосвязи понятий, относящихся к одной области деятельности или познания.

Пример

Рассмотрите граф понятий темы «Четырёхугольники» из курса геометрии (рис.6). Не правда ли, хорошая «шпаргалка»?

Рис.6. Граф понятий темы «Четырёхугольники»

В практической деятельности модели в форме графов часто используются для представления видов и порядка выполнения работ. Возможно, вам знакомы такие термины, как «сетевой график работ», «сетевой график строительства». Часто наряду со словесным или табличным описанием сетевые графики сопровождаются и изображением в виде графа, вершинами которого являются конкретные виды работ, а дугами задаётся возможный порядок их выполнения.

Пример

Сетевые графики строительства хорошо демонстрируют, какие работы могут выполняться одновременно, а какие требуют обязательного завершения предыдущих этапов. Анализируя такие графы, можно рассчитать время, необходимое для завершения всей работы, спланировать, сколько, когда и на какие работы направить специалистов и технику, определить наиболее «узкие» участки и уделить им особое внимание.

	1	2	3	4	5
1		а		b
2	а			с
3				f	d
4	b	с	f		e
5			d	e

Для машинной обработки более удобным является символическое представление графов в виде списка рёбер с указанием, какие вершины это ребро соединяет, а также табличное представление, где строки и столбцы — названия вершин, а значения ячеек указывают на то, соединены данные вершины или нет.

Пример

Графы, представленные на рис.7 могут быть описаны, например, следующими способами. Символическая запись: а(1,2) b(l,4) c(2,4) d(3,5) e(4,5),(3,4)

Табличная запись:

Рис.7. Графы, имеющие одинаковые описания в виде таблицы и символической записи

Представление данных в форме дерева

Особым видом графа является дерево. Данная форма модели применяется тогда, когда элементы моделируемого объекта находятся в состоянии какого-либо подчинения и соподчинения, когда есть отношение иерархичности.

Пример

Модель управления предприятием (школой, театральным коллективом и т. д.) очень удобно представлять в виде дерева.

Пример

Вам хорошо известно понятие «родословное дерево» и вы можете изобразить в такой форме ваши родственные отношения.

Пример

Каталог файлов на диске, также как и библиотечный каталог — примеры информационных моделей в форме дерева. Дерево — это граф, предназначенный для отображения таких связей между объектами, как вложенность, подчиненность, наследование и т. п.

Строится он следующим образом

Сначала рисуем «главную» вершину, которая не зависит ни от одной другой вершины. Эта вершина называется корнем дерева и является единственной вершиной 1-го уровня. Далее добавляем вершины 2-го уровня. Их может быть сколько угодно, и все они обязательно связаны с корнем — вершиной 1-го уровня, но не связаны между собой. На следующем шаге добавим вершины 3-го уровня. Каждая из них будет связана ровно с одной вершиной 2-го уровня (больше ни с одной другой вершиной). К любой вершине 2-го уровня может быть подсоединено сколько угодно вершин 3-го уровня (в том числе, ни одной). Следующий шаг — добавка вершин 4-го уровня, каждая из которых будет связана ровно с одной вершиной 3-го уровня (и не связана больше ни с чем). И так далее. На каждом шаге добавляем вершины очередного уровня, каждая из которых будет связана ровно с одной вершиной предыдущего уровня и не будет иметь никаких иных связей. Полученный граф напоминает ветвящийся куст, который «растет сверху вниз»: верхние уровни имеют меньшие номера, нижние — большие. Вообще говоря, дерево может быть и неориентированным графом, но чаще дерево ориентировано, причем дуги направлены от верхних вершин к нижним. Верхняя вершина называется предком для связанных с ней нижних вершин, а нижние вершины — потомками соответствующей верхней вершины. На любом дереве существует единственная вершина, не имеющая предка, — корень — и может быть сколько угодно вершин, не имеющих потомков, — листьев. Все остальные вершины имеют ровно одного предка и сколько угодно потомков. Если не принимать во внимание направленность связей, то в дереве из любой вершины можно по линиям дойти до любой другой вершины, причем по одному единственному пути. В виде дерева удобно изображать системы, в которых нижние вершины в каком-то смысле «подчинены» верхним. Верхняя вершина может изображать начальника, нижние — подчиненных; верхняя — систему, нижние — ее компоненты; верхняя — множество объектов, нижние — входящие в него подмножества; верхняя вершина — предка, нижние — потомков и т. д. Формализация в случае построения дерева (иерархического графа) сводится к выявлению основного (главного, центрального) элемента рассматриваемого объекта (вершина нулевого уровня, которую часто называют корнем), элементов, которые находятся в непосредственном подчинении от основного (вершины 1-го уровня). Затем определяются вершины, находящиеся в непосредственном «подчинении» от вершин 1-го уровня (вершины 2-го уровня) и так далее. Изображать построенное дерево отношений можно в любом направлении — это уже дело эстетического вкуса разработчика модели. В научной и учебной деятельности с помощью деревьев часто представляют классификацию изучаемых объектов.

Классифицирование — распределение объектов по классам в зависимости от их общих признаков, фиксирующее закономерные связи между классами объектов в единой системе данной отрасли знания.

Классификация (от лат. classis — разряд + facere — делать) — система соподчиненных понятий (классов объектов, явлений) в какой-либо отрасли знания, составленная на основе учёта общих признаков объектов и закономерных связей между ними.

Классификация позволяет ориентироваться в многообразии объектов и является источником знания о них. Очень важен выбор основания классификации — то есть признака, на основании которого объекты разбиваются на классы. Выбор разных оснований приводит к разным классификациям.

Пример

На рис.8 вы видите классификацию, предложенную Григорием Великим, которая призвана была показать, что человек имеет что-то общее со всеми видами существующих в мире вещей, и поэтому его справедливо называют «вселенной в миниатюре». Обратите внимание, что объекты здесь разбиваются всегда на два класса. Такая классификация носит название дихотомической.

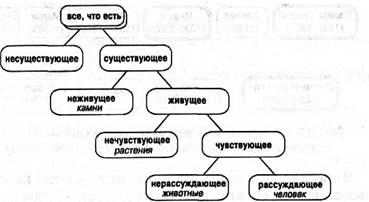
Рис.8. Классификация «того, что есть» Григория Великого

Пример

Представленная на рис.9 классификация принтеров построена с использованием различных оснований деления

Рис.9 Классификация принтеров

Пример

Важным видом исторических классификаций является построение родословных или генеалогических деревьев. Они бывают самого разного вида: с указанием только прямых потомков (рис.10); с включением жён (мужей) и их родственников и др.

Рис.10 Родословное дерево великих и удельных князей Владимирских и Московских, XIII—XIV века (фрагмент)

В скобках приведены известные даты жизни; крест указывает на год смерти; двойным контуром обведены имена князей, занимавших московский престол. Рассмотренные выше реляционная (табличная), сетевая (графовая) и иерархическая (древовидная) модели являются основными для представления данных в базах данных, а программные комплексы, которые позволяют создавать, обновлять, сохранять базы данных и обслуживать запросы пользователей к ним, называются соответственно реляционной, сетевой, иерархической системами управления базами данных (СУБД). При описании сложных объектов, как правило, используется комбинация различных моделей данных.

Вывод:

Формализация текстовой информации:

• облегчает и ускоряет процесс её обработки;

• позволяет получить количественные оценки;

• обеспечивает однозначность понимания текста;

• способствует лучшему восприятию сведений, содержащихся в тексте;

• помогает сравнить по формальным критериям ситуацию, описанную в тексте, с реальной и принять правильное решение.

Формализовать можно как оформление текста, так и его содержание.

Формализация оформления сводится к использованию бланков, формуляров, шаблонов заранее определённой и часто законодательно утверждённой стандартной формы.

Шаблон документа — стандартная форма документа, встречающегося в сфере делопроизводства.

Реквизитами документа называются обязательные данные, которые необходимо отразить в документе.

Целью формализации содержания текста является его однозначное понимание. Это очень важно в юридической практике, в научной и управленческой деятельности, например, при формулировании определений, составлении законов, договоров, приказов, распоряжений и т.п.

Таблицы — удобная для анализа и обработки и наглядная форма представления информации. Таблицы, в которых отражается одно свойство, характеризующее два или более объектов, называются таблицами типа «объект-объект». Таблицы, в которых отражаются несколько свойств объекта, а все объекты принадлежат одному множеству, называются таблицами вида «объект-свойство». Комбинирование в одной таблице нескольких таблиц вида «объект-объект» и «объект-свойство» позволяет построить таблицы более сложного вида, например, «объекты-свойства-объекты». Таблица характеризуется:

• названием (а если таблиц несколько, то ещё и номером),

• количеством столбцов и их названиями (заголовками столбцов),

• количеством строк и их названиями (заголовками строк),

• содержимым ячеек, находящихся на пересечении строк и столбцов.

В случае многоуровневых заголовков строк и столбцов уровни заголовков столбцов называются ярусами, уровни заголовков строк — ступенями.

Основными элементами таблицы являются:

• поля — столбцы таблицы, содержащие, как правило, данные одного типа;

• реквизиты — конкретные значения, находящиеся в ячейках таблицы на пересечении строк и столбцов.

Этапы приведения к табличному виду:

1. анализ информации и выделение объектов, о которых идет речь;

2. выделение свойств объектов и/или отношений между ними;

3. определение того, можно ли объекты объединить в некоторые подмножества, и в зависимости от этого определение количества уровней и ступеней в заголовках;

4. определение общего количества столбцов и порядка их расположения;

5. определение наименований столбцов и типа данных, которые там будут располагаться;

6. выбор порядка размещения строк и определение названия каждой строки таблицы;

7. занесение в ячейки таблицы реквизитов-данных (построчно или по столбцам).

Граф — совокупность точек, соединённых между собой линиями. Эти точки называют вершинами графа. Линии, соединяющие вершины, называются дугами, если задано направление от одной вершины к другой, или рёбрами, если направленность двусторонняя. Граф называется взвешенным, если вершины или рёбра (дуги) характеризуются некоторой дополнительной информацией — весом вершины или ребра (дуги). Граф однозначно задан, если заданы множество его вершин, множество рёбер (дуг) и указано, какие вершины какими рёбрами соединены.

Формализация при построении графа включает в себя следующие этапы:

• выявление всех элементов объекта;

• определение характеристик элементов (названий, номеров, весов и т. п.);

• установление наличия и вида связей (односторонняя или двухсторонняя) между элементами;

• определение характеристик связей — весов рёбер и дуг;

• выбор формы изображения вершин и рёбер, ввод условных обозначений в случае необходимости;

• представление выделенных элементов и связей в графическом виде.

Для компьютерного моделирования более удобным является символическое и/или табличное задание графа. Символическое задание графа — перечисление всех его рёбер с указанием вершин, которые они соединяют, либо перечисление всех вершин с указанием исходящих из них рёбер.

Дерево — особый вид графа, применяемый при моделировании объекта, элементы которого находятся в отношении иерархии (подчинения и соподчинения). Корнем дерева называется вершина, соответствующая основному (центральному, главному, родовому) элементу моделируемого объекта. Листьями дерева называют вершины графа, у которых нет «подчинённых» вершин. Формализация при построении дерева сводится к выявлению основного элемента рассматриваемого объекта (вершина нулевого уровня — корень дерева), элементов, которые находятся в непосредственном подчинении у основного элемента (вершины 1-го уровня), элементов, находящихся в непосредственном подчинении у вершин 1-го уровня (вершины 2-го уровня) и т. д. Классификация — система соподчинённых понятий (классов объектов, явлений) в какой-либо отрасли знания, составленная на основе учёта общих признаков объектов и закономерных связей между ними. Представляется чаще всего в виде иерархического графа (дерева) или таблицы. Реляционная (табличная), сетевая (графовая) и иерархическая (древовидная) модели являются основными для представления данных в базах данных. Программные комплексы, которые позволяют создавать, обновлять, сохранять базы данных и обслуживать запросы пользователей к ним, называются соответственно реляционной, сетевой, иерархической системой управления базами данных (СУБД). Большинство существующих автоматизированных баз данных являются базами данных реляционного типа.

12	Поделиться:

Воспользуйтесь поиском по сайту: