 |
Задания контрольной работы
|
|
|
|
БЕЛКООПСОЮЗА
Рассмотрено Утверждаю
на заседании цикловой
комиссии Общеобразовательных Зам.директора по
и общепрофессиональных учебной работе
дисциплин _________ С.В.Сочнев
Председатель _________ Е.И.Фоминых «___» _________2016г.
Протокол №____ от ________2016г.
ЗАДАНИЯ ДОМАШНЕЙ
КОНТРОЛЬНОЙ РАБОТЫ
По дисциплине
«МАТЕМАТИКА»
Для учащихся 1 курса заочного отделения
Для специальности: «Экономика и организация производства»
Разработал
ТютяноваВ.А.
Гомель 2016
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Дисциплина «Математики» занимает особое место среди других дисциплин учебного плана специальности «Экономика и организация производства». Знания, полученные учащимися при изучения дисциплины «Математика», должны стать базовыми. т.к. являются теоретической основой статистических дисциплин, которые непосредственно используются при изучении массовых экономических явлений, обработке экономической информации выявлении статистических закономерностей сложных и многообразных экономических процессов. Поэтому осмысленное изучение курса играет важную роль в формировании навыков экономического моделирования будущих специалистов.
Программа дисциплины «Математика» включает изучение линейной алгебры, введение в математический анализ, дифференциальное и интегральное исчисление функции одной переменной, элементы теории вероятности и математической статистики, понятие о линейном программировании. Наряду с приобретением учащимися знаний по названным разделам высшей математики, изучение дисциплины должно способствовать развитию их логического мышления, математической культуры, формированию профессиональных навыков.
|
|
|
В результате изучения дисциплины учащиеся должны знать:
- место математики в системе знаний экономиста;
- понятие математической модели и принципы се построения;
- определения матрицы и определителя, правила выполнения действий над ними;
- определения функции, предела, непрерывности функции, производной, дифференциала, интеграла;
- определение случайных событий и вероятность события;
- основные понятия математической статистики;
- что такое задачи линейного программирования;
дол ж ны уметь:
- вычислять определители, выполнять действия над матрицами;
- решать системы линейных неравенств;
- решать системы линейных уравнений;
- вычислять пределы функции, производные, определенные и неопределенные интегралы;
- решать вероятностные задачи.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО РЕШЕНИЮ ЗАДАЧ КОНТРОЛЬНОЙ РАБОТЫ
ЗАДАЧА 1.
Вычислить определители
а)  ; б)
; б)  в)
в) 
Решение:
а) Определитель второго порядка вычисляется но формуле
∆ = α11·α22 – α12·α21
Используя эту формулу, имеем
 = 4·8 - 3·6 = 14
= 4·8 - 3·6 = 14
б) Определитель третьего порядка вычисляется по формуле:
∆ = (α11·α22· α33 + α12·α23· α31+ α13·α21· α32) – (α11·α23· α32 + α12·α21· α33+ α13·α31· α22)
Для запоминания этой формулы удобно пользоваться следующей схемой, на которой элементы, произведения которых надо подсчитать, соединяются линиями по три:

Используя эту формулу получаем:
 = (6∙2∙3 + 7∙4∙5 + 0∙1∙3) – (7∙2∙3 + 6∙1∙5 + 0∙4∙3) = (36 + 140+0) – (42 + 30 + 0) = 176 -72 = 104
= (6∙2∙3 + 7∙4∙5 + 0∙1∙3) – (7∙2∙3 + 6∙1∙5 + 0∙4∙3) = (36 + 140+0) – (42 + 30 + 0) = 176 -72 = 104
в) Для вычисления определителя четвертого порядка используем свойства определителей:
1. значение определителя не изменится, если все его строки заменить соответствующими столбцами, или наоборот, столбцы - строками;
2. если два столбца (две строки) поменять местами, то определитель изменит свой знак на противоположный;
|
|
|
3. если определитель содержит строку (столбец), все элементы в которой равны 0, то определитель тоже равен 0;
4. определитель с двумя одинаковыми строками (столбцами) равен 0;
5. если все элементы какой либо одной строки (одного столбца), умножить на одно и то же число к ≠ 0, то значение определителя также возрастет в к раз;
6. если ко всем элементам какой-либо строки определителя прибавить соответствующие элементы другой строки, умноженные на одно и то же число к, то значение определителя не изменится;
7. если ко всем элементам какого-либо столбца определителя прибавить соответствующие элементы другого столбца, умноженные на одно и то же число к, то значение определителя не изменится.
Вполне понятно, что при вычислении определителей порядка выше третьего в соответствии с формулой разложения определителя по какой-либо строке (какому-либо столбцу) объем вычислений существенно возрастает. Так использование названной формулы сведет вычисление определителя четвертого порядка к вычислению четырех определителей третьего порядка, вычисление определителя пятого порядка - к вычислению пяти определителей четвертого порядка и т.д. В то же время использование свойств определителя в ряде случаев позволяет достаточно быстро получить требуемый результат. Так, для вычисления определителя


попытаемся в каком-либо столбце или строке (например, в 3-ей сроке) добиться максимально возможного количества нулей. С этой целью проведем следующее преобразование: от элементов 4-ого столбца вычтем соответствующие элементы 2-ого столбца, умноженные на 2.

Полученный таким образом определитель легко вычисляется разложением по третьей строке:
∆ = 0·А31+ 3·А32 + 0·А33+0·А34
Поскольку три из четырех слагаемых обращаются в ноль, остается вычислить только одно алгебраическое дополнение А32:
∆ = 3·А32 = 3· (-1)3+2 · 
=-3· ((2· 3· (-4)+6· 3· 4+0· 1· 0)-(3· 3· 0 + 0· 6· (-4)+2· 1· 4))=
= -3· ((-24+72+0)-(0+0+8))=-3-(48-8)=-3-40 = -120.
ЗАДАЧА 2
Решить систему линейных уравнений методом Крамера

Решение:
Составим матрицу системы А= 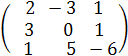 и
и
расширенную матрицу В= 
Вычислим определитель матрицы А
det А =  =(2∙0∙(-6) + 1∙5∙3 + 1∙1∙(-3))– (1∙0∙1 + 2∙5∙1 + 3∙(-3)∙(-6)) = -52
=(2∙0∙(-6) + 1∙5∙3 + 1∙1∙(-3))– (1∙0∙1 + 2∙5∙1 + 3∙(-3)∙(-6)) = -52
|
|
|
det А ≠ 0, следовательно ранг матрицы системы и ранг расширенной матрицы равны 3. Поскольку r (А) = r (В) = 3, система совместна, а так как количество переменных в системе тоже равно 3, система имеет единственное решение. Найдем решение системы методом Крамера. Заметим, что определитель ∆ уже найден: ∆ = det А = -52. Остается вычислить определители ∆1, ∆2, ∆3
∆1 = 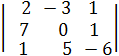 = (2∙0∙(-6) + 1∙5∙7 + 1∙1∙(-3))– (1∙0∙1 + 2∙5∙1 + 7∙(-3)∙(-6))=-104
= (2∙0∙(-6) + 1∙5∙7 + 1∙1∙(-3))– (1∙0∙1 + 2∙5∙1 + 7∙(-3)∙(-6))=-104
∆2 =  = (2∙7∙(-6) + 1∙1∙3 + 1∙1∙2)– (1∙7∙1 + 2∙1∙1 + 3∙2∙(-6))=-52
= (2∙7∙(-6) + 1∙1∙3 + 1∙1∙2)– (1∙7∙1 + 2∙1∙1 + 3∙2∙(-6))=-52
∆3 =  = (2∙0∙1 + 2∙5∙3 + 1∙7∙(-3))– (1∙0∙2 + 2∙5∙7 + 3∙(-3)∙1)=-52
= (2∙0∙1 + 2∙5∙3 + 1∙7∙(-3))– (1∙0∙2 + 2∙5∙7 + 3∙(-3)∙1)=-52
Далее вычисляем значения неизвестных x1, х2, х3 по формулам Крамера:
x1=  x2 =
x2 =  x3=
x3= 
Ответ: x1 = 2; х 2 = 1; х 3 = 1
ЗАДАЧА З
Найти производные и дифференциалы функций
а)у = 7х3 + 2х; б) у = 
Решение:
При вычислении производной следует использовать следующие формулы и правила дифференцирования:
1. (U±V)'=U'±V'; 3. (UV) ' =U'V+UV';
2. (CU)'=Cu', где С — const 4. 
Производная сложной функции вида y=f(g(x)) равна
у'х =f(g(х)) g'(X)
Таблица производных:
| с'=0 | (sin)'=cosx | (arcsinx)' = 
|
| (kx+b)' = k | (cosx)'= - sin x | (arccosx)' = 
|
| Хn= n x n-1 | (ex) '=ex | (lnx) '= 
|
Дифференциалом функции у = f(x) называют главную линейную относительно ∆х часть приращения ∆ у.
Дифференциал функции обозначают dy или df(x).
Дифференциал функции вычисляют по формуле
dy = у′ dх
С учетом приведенных выше сведений решение примеров а) и б) можно записать следующим образом:
a) у′= (7х3 + 2х) ′=21 х2 + 2; dy= 21 х2 + 2
б)) у′= ( ) ′= (
) ′= ( )ln2 (5х + 3) ′= 5∙
)ln2 (5х + 3) ′= 5∙  ln 2; dy = 5∙
ln 2; dy = 5∙  ln 2 dх ;
ln 2 dх ;
ЗАДАЧА 4
Вычислить определенные интегралы
a) 
b) 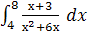
Решение:
При вычислении неопределенных интегралов используются следующие формулы:

| 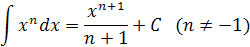
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||
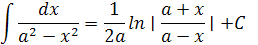
| 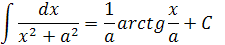
|
Существует ряд методов интегрирования функций. Под непосредственным интегрированием понимают метод, при котором с помощью тождественных преобразований подинтегральной функции и использования свойств 3—4 неопределенного интеграла удается свести искомый интеграл к одному или нескольким табличным интегралам. Непосредственное интегрирование возможно далеко не всегда, поэтому нередко приходится использовать и другие методы.
|
|
|
Метод подстановки заключается в том, что путем замены переменной х = φ (t) dx = φ'(t) dt получают интеграл вида 
При этом стремятся подобрать такую замену переменной, чтобы полученный интеграл был более простым (например, вычислялся непосредственным интегрированием).
Покажем применение этого метода на примере вычисления интеграла
 , если известно, что
, если известно, что  F(x) +C
F(x) +C
Введем замену ах+b = t, тогда a∙ dx = dt или dx=dt /a. С учетом этого имеем:
 F(x) +C =
F(x) +C =  F(ax+b)+C
F(ax+b)+C
Таким образом, если  F(x) +C, то
F(x) +C, то  F(ax+b)+C
F(ax+b)+C
Интегрирование функции по частям выполняется по формуле:

Для вычисления определенных интегралов используется формула Ньютона-Лейбница:

где F(a) и F(6) - значения любой из первообразных F (х) + С при х = а
и при x = bсоответственно.
Методы вычисления определенных интегралов аналогичны соответствующим методам для неопределенных интегралов. Некоторые отличия имеются только при использовании для вычисления интегралов подстановки х = φ (t) dx = φ'(t) dt. Здесь пределы интегрирования a и b, соответствующие изменению переменной х, должны быть заменены на числа α и β, соответствующие изменению переменной t. Значения α и β при этом находятся из соотношения a= φ (α), b= φ (β). С учетом этого получаем
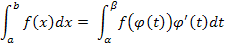
С учетом приведенных выше сведений решение примеров а) и б) запишется в виде:
а) интеграл берется методом непосредственного интегрирования
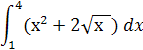
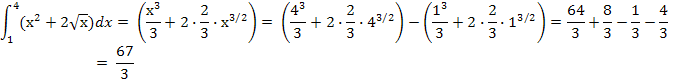
б) интеграл берется с помощью подстановки:
 (2x +6) dx = dt
(2x +6) dx = dt
Найдем пределы интегрирования для переменной t:
х =4: t = 42 +6∙4=40
х = 8: t = 82 +6∙8=112
Тогда 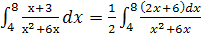 =
=  112-ln40)=
112-ln40)= 
ЗАДАЧА5.
а) В урне находятся 5 красных и 7 синих шаров. Найдите вероятность того, что два наугад вытянутые из урны шара окажутся разных цветов
1) красными;
2) разных цветов.
б) Стрелок при единичном выстреле поражает цель с вероятностью 0,8. Найдите вероятность того, что, сделав три выстрела, стрелок
1) не попадет в цель;
2) попадет в цель ровно один раз;
3) попадет в цель хотя бы один раз
УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Вариант контрольной работы определяется по таблице в зависимости от двух последних цифр шифра личного дела учащегося.
При выполнении контрольной работы следует строго придерживаться следующих правил:
- контрольная работа выполняется в тетради с пронумерованными страницами и
с полями для замечаний преподавателя;
- для каждой задачи указывается ее номер, переписывается условие, даются под-
|
|
|
робные комментарии по ходу решения, в конце задачи записывается ответ;
- после решения всех задач контрольной работы следует указать список литера-
туры, поставить дату и подпись.
Таблица выбора варианта контрольной работы
| Предпоследняя цифра шифра | Последняя цифра шифра | |||||||||
ЗАДАНИЯ КОНТРОЛЬНОЙ РАБОТЫ
1-10. Вычислить определитель  , разложив его по элементам
, разложив его по элементам  -й строки.
-й строки.
1.  ,
, 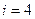 2.
2.  ,
,  3.
3.  ,
, 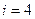
4.  ,
,  5.
5.  ,
,  6.
6.  ,
, 
7.  ,
,  8.
8.  ,
, 
9.  ,
, 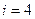 10.
10.  ,
, 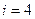
|
|
|


