Использование функции genfit

Учебная практика

Методические указания, занятие №3

Нахождение вида функциональной зависимости экспериментальных данных

 

Задание простейших математических функций

Для программирования простейших математических функций в MathCad необходимо ввести имя функции, в скобках её параметры и оператор присваивания. Таким образом, запись F(x):= предполагает, что выражение после оператора присвоения определяет функцию с именем F, которая зависит от переменной x. Например,

присваивает функции F(x) значение 2x²+3.

В дальнейшем для того чтобы получить значение функции в некоторой точке, например, x=3, необходимо будет записать F(3). В рассмотренном примере данное значение будет равным 21.

 

ЗАДАНИЕ Запрограммировать функции в зависимости от варианта. Получить результат в указанных точках.

 

	Предпоследняя цифра зачетки
Последняя цифра зачетки

 

Варианты заданий:

Номер варианта	f(x)	Значения x	g(a, b)	Значения (a, b)
	1/(2x2+2)	5; -8; 11	a∙eb	(-2, 0,5); (4, 2); (1, -2)
	sin(3x)	4; 12; 19	logab	(10, 3); (e, 10); (5, 14)
	2tg(x)	2; -1; 12	18a/2b	(-3, 2); (2, 1); (15, 3)
	ctg(x)	2; -1; 12	14a+2b	(-1, 2); (2; 1); (1, 0,5)
	ln(x)	e; 1; 2	a∙sin(b)	(1, 2); (-2; 1); (1, 0,5)
	ex	0,5; 1; 3	a∙cos(b)	(-3, 2); (2, 1); (10, 3)
	lg(x)	2; 1; 10	sin(a)+cos(b)	(4, 5); (1; 0,5); (2, 7)
	cos(x)	4; 12; 1		(0, 5); (1; 0,5); (2, 7)
	sh(x)	1; 3; 0,5	a2-3b	(0,5, 2); (2; 1); (1, 0,5)
	сh(x)	1; 3; 0,5		(2, 0); (1; -0,5); (2, 3)
	1/x	2; 4; 5	cos(a)/b	(-2, 0,5); (4, 2); (1, -2)
	1/x2	-1; 2; 4	sin(b)/a	(-2, 0,5); (4, 2); (1, -2)
	1/(x2+1)	4; 2; 1	a∙tg(b)	(0,5, 2); (2; 1); (1, 0,5)
	lg(x)/x	2; 1; 10	ch2(a) –sin(eb)	(0,5, 2); (2; 1); (1, 0,5)
	x/(x2+1)	3; 2; 0,5	tg(a)+cos(b)	(4, 5); (1; 0,5); (2, 7)
	x3/(x+1)	2; 1; 10	2a/lg(b)	(2, 2); (-1; 5); (2, 10)
	2x2/(x-1)	4; 12; 1	101/a + sh(b)	(0,5, 2); (2; 1); (1, 0,5)
	ln(x)/x	e; 1; 2	esin(a)+2b	(1, 2); (2; 1); (0, 0,5)
	sin(x)+ch(x)	5; 2; 0		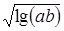(2, 5); (0,5, 2); (4, 9)
	ex/x	1; -1; 0,5	1/(sin2(a)+b)	(4, 5); (1; 0,5); (2, 7)
	e2lgx	2; 1; 10		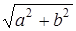(0, 5); (2; 3); (2, 0)
	cos(x)+sh(x)	1; -2; 0	lg(a)/b	(1, 2); (2; 1); (10, 0,5)
	3x/lg(x)	2; 10; 4		(0,5, 2); (2; 1); (1, 0,5)
		-1; 2; 4	ctg(a)+ecos(b)	(4, 5); (1; 0,5); (2, 7)
	1/(lg(x)+1)	2; 1; 10	cos2(a) -3b	(0,5, 2); (2; 1); (1, 0,5)
	101/x	1; 2; 0,5	cos(a)+a∙sh(b)	(0,5, 2); (2; 1); (1, 0,5)
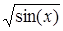
		2; 4; 5	2a+lg(b)	(2, 2); (-1; 5); (2, 10)
	5x+2	0; 1; 0,5	a/sin(b)	(1, 2); (2; 1); (0, 0,5)
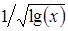
		2; 1; 10	sin2(a)+cos(b2)	(4, 5); (1; 0,5); (2, 7)

 

Указание:

‑ аргументы всех тригонометрических и гиперболических функций считать в радианах.

 

Функция также может быть задана в виде вектора или матрицы, например

Использование функции linfit

Формат *.prn является одним из форматов данных, с которыми работает MathCad, и представляет собой структурированный ASCII-файл. Такой файл является текстовым и содержит цифровые значения, причем между числами в каждой строке ставится разделитель.

 

Если предполагается, что данные могли бы быть смоделированы в виде линейной комбинации произвольных функций , ,… , 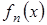то есть

,

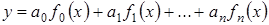то для нахождения неизвестных коэффициентов , , …, используется функция linfit. Пример применения функции linfit приведен на рисунке 1.

Рисунок 1 – Пример применения функции linfit

 

Здесь предполагается, что есть два вектора x и y, содержащих экспериментальные точки. Линейная комбинация состоит из трех функций вида

, ,

и задается в MathCad векторной функций F(x).

Функция linfit(x, y, F) возвращает вектор, содержащий неизвестные коэффициенты , , линейной комбинации функций из F. Этот вектор записывается в переменную S. Линейная комбинация задается функцией g(t) путем умножения вектора F на вектор S.

Для построения графика функции g необходимо задать массив точек по оси абсцисс, причем для гладкости графика точки должны располагаться достаточно плотно. Это реализуется с помощью записи

,

которая подразумевает создание массива точек от 0 до 1 с шагом 0,025.

 

ЗАДАНИЕ: Подобрать вид функциональной зависимости по экспериментальным данным с помощью функций linfit для значений R, полученных в результате выполнения задания из пункта 4 занятия №1.

Указание:

‑ в линейной комбинации использовать не менее трех функций;

‑ для подбора возможных функций, входящих в линейную комбинацию воспользоваться графиком экспериментальных точек.

 

ЗАДАНИЕ: Построить совмещенные графики:

‑ подобранной функциональной зависимости и экспериментальных точек;

‑ подобранной функциональной зависимости и теоретических данных.

 

Использование функции genfit

Если предполагается, что данные могут быть смоделированы в виде сложной функции, например,

,

то для нахождения неизвестных коэффициентов , , …, используется функция genfit. Пример применения функции genfit приведен на рисунке 2.

Здесь также предполагается, что есть два вектора x и y, содержащих экспериментальные точки. Данные приближаются функцией вида

.

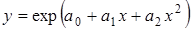Для вызова функции genfit необходимо задать ее и ее производные по каждому из неизвестных коэффициентов , , . Данные функции задаются вектором F(z, a).

Кроме того, необходимо задать начальное приближение коэффициентов. Это осуществляется с помощью вектора vg.

 

Рисунок 2 ‑ – Пример применения функции genfit

 

Функция genfit(x, y, vg, F) возвращает вектор, содержащий неизвестные коэффициенты , , , которые обеспечивают наилучшее приближение данных x и y. Этот вектор записывается в переменную S. Задание функции осуществляется подстановкой вектора S в функцию F и выделением первого элемента этого вектора

.

ЗАДАНИЕ: Подобрать вид функциональной зависимости по экспериментальным данным с помощью функций genfit для значений L, полученных в результате выполнения задания из пункта 4 занятия №1.

Указания:

‑ рассмотреть функции из ряда:

, , ;

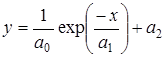‑ для подбора вида функции и начального приближения воспользоваться графиком экспериментальных точек и наложить на него график получаемой с использованием genfit функции.

 

ЗАДАНИЕ: Построить совмещенные графики:

‑ подобранной функциональной зависимости и экспериментальных точек;

‑ подобранной функциональной зависимости и теоретических данных.

Поделиться:

Воспользуйтесь поиском по сайту: