Основные сведения об оптимальном кодировании

Лабораторная работа № 2

Оптимальное кодирование

Основные сведения об оптимальном кодировании

Кодированием информации называется операция преобразования сообщений, состоящих из символов первичного алфавита, в определенную последовательность символов вторичного алфавита (элементарных символов). Обратная операция, восстанавливающая исходное сообщение по элементарным символам называется декодированием. Любому дискретному сообщению можно приписать некоторое число – его код. Тогда передача сообщений сводится к передаче кодов. Очевидно, что для восстановления по кодам сообщений они должны быть однозначно декодируемыми (разделимыми). Таким свойством обладают префиксные коды.

Префиксные коды – это такие коды, в которых ни одна более короткая комбинация не является началом более длинной комбинации, что позволяет производить однозначное декодирование, даже если последовательность кодов не содержит разделителей между кодами.

Для существования двоичного разделимого кода, содержащего N кодовых слов, состоящих из символов 0 и 1, с длинами n ₁, n ₂, …, n_N, необходимо и достаточно, чтобы выполнялось неравенство Крафта:

.

Дискретный источник сообщений, который описывается моделью с независимыми символами сообщений, называется дискретным источником без памяти. Для любого дискретного источника без памяти X с конечным алфавитом и энтропией H (X) существует двоичный код, в котором средняя длина кодового слова удовлетворяет неравенству

,

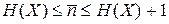т.е. средняя длина кодового слова не может быть меньше энтропии источника сообщений. Кроме того, доказано, что для блока длины L существует двоичный префиксный код, в котором средняя длина кодового слова на один символ удовлетворяет неравенству

,

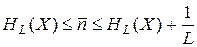где . Последнее неравенство позволяет утверждать, что существуют такие способы кодирования для достаточно длинного сообщения, что средняя длина кодового слова может быть сделана сколь угодно близкой к величине H (X).

Так как минимально достижимой длиной кодового слова на символ является величина, равная значению энтропии H, то избыточность кода можно определить по формуле .

Одно и то же сообщение можно закодировать различными способами. Оптимальным считается такой код, при котором на передачу сообщений затрачивается минимальное время. Если при этом на передачу каждого элементарного символа кода тратиться одно и то же время, то оптимальным будет код, имеющий минимально возможную длину.

Принципы построения оптимальных кодов:

1. каждый элементарный символ должен переносить максимальное количество информации, для этого необходимо, чтобы элементарные символы в закодированном тексте встречались в среднем одинаково часто, т.к. энтропия в этом случае будет максимальной;

2. необходимо кодируемым символам, имеющим большую вероятность, присваивать более короткие кодовые слова.

При равномерном распределении вероятностей символов в сообщении оптимальным будет равномерный код. При равномерном кодировании каждому символу алфавита сообщений присваивается код, состоящий из ]log₂ n [ двоичных значений, где n – число различных кодируемых символов, а ]log₂ n [ – ближайшее целое, не меньшее n. Это можно сделать, например, сопоставив каждому символу число от 0 до n – 1 в двоичной системе счисления.

Одним из способов оптимального кодирования является метод Шеннона-Фано. Для построения кода Шеннона-Фано все символы алфавита сообщений записывают в порядке убывания вероятностей их появления. Полученную ранжированную (упорядоченную) последовательность символов разбивают на две группы так, чтобы суммы вероятностей групп были примерно одинаковыми. Для символов первой группы в качестве первого кодового символа присваивают 0, а для символов второй группы – 1. Полученные группы символов сообщений опять разбивают таким же образом на две подгруппы и опять кодируют. Это продолжается до тех пор, пока в последних подгруппах не останется по одному символу сообщений. Пусть, например, имеется алфавит сообщений

X = (x ₁, x ₂, x ₃, x ₄, x ₅, x ₆, x ₇, x ₈)

с распределением вероятностей появления символов

.

В результате кодирования по методу Шеннона-Фано символов алфавита X будут получены коды из таблицы 1.

Таблица 1

Кодирование Шеннона-Фано

X	P	Шаг	Коды
x 1	1/4			¾	¾
x 2	1/4			¾	¾
x 3,	1/8				¾
x 4	1/8				¾
x 5	1/16
x 6	1/16
x 7	1/16
x 8	1/16

 

Поделиться:

Воспользуйтесь поиском по сайту: