Определение напряжений при кручении стержней с круглым поперечным сечением

Рассмотрим стержень с круглым поперечным сечением (рис. 6, а), один конец которого закреплен, а другой нагружен парой сил с моментом Т_е. В результате действия момента внешних сил Т_е возникает деформация кручения. Наблюдая при кручении характер искажения прямоугольников координатной сетки, нанесенной на боковой поверхности круглого стержня, обнаружили: прямоугольная сетка превратится в сетку, состоящую из параллелограммов, что свидетельствует о наличии касательных напряжений в поперечных, а с учетом закона парности касательных напряжений и в продольных сечениях; контуры поперечных сечений в процессе деформации остаются плоскими, расстояния между ними не изменяются, а первоначальные прямолинейные образующие, нанесенные на боковую поверхность, превращаются в винтовые линии; диаметры торцового сечения повернутся на некоторый угол φ относительно своего начального положения, оставаясь прямой линией. Эти наблюдения позволили составить представление о механизме деформации кручения. Постоянство длины и диаметра деформируемого стержня свидетельствует об отсутствии нормальных напряжений в поперечных и продольных сечениях. Так как в поперечных и в продольных сечениях действуют только касательные напряжения, напряженное состояние в точках скручиваемого стержня представляет собой чистый сдвиг. Поперечные сечения, оставаясь плоскими, поворачиваются вокруг оси стержня относительно друг друга на некоторый угол, сохраняя длину и прямолинейность своих радиусов.

Выделим двумя поперечными сечениями элемент (рис. 6. б) скручиваемого стержня длиной dx. В результате деформации одно сечение повернется относительно другого на угол dφ. Будем считать левое сечение элемента dx неподвижно закрепленным. Тогда dφ – угол поворота правого торцового сечения вокруг продольной оси. Образующую АВОО₁ можно представить как параллелепипед длиной dx с бесконечно малыми основаниями АО₁ и ВО. В результате деформации этот параллелепипед займет положение АВ'ОО₁. Величина ВВ' = γdx = ρdφ представляет собой абсолютный сдвиг грани В на поверхности стержня относительно грани А в направлении, перпендикулярном радиусу стержня. Величина абсолютного сдвига точек основания ОВ параллелепипеда зависит от их расстояния ρ до оси стержня. Сдвиг равен нулю на оси стержня и максимален, т.е. равен ВВ' на поверхности. Угол сдвига соответственно будет равен

γ = (dφ/dx)ρ, (22)

где dφ/dx – относительный угол закручивания. На основании закона Гука для сдвига можно записать

τ_ρ = G·γ = G(dφ/dx)ρ, (23)

где G – модуль упругости материала стержня при сдвиге.

 

в

б

Эпюра τ

а

Te

Рис. 6

 

Величина касательных напряжений в каждой точке сечения прямо пропорциональна расстоянию ρ от точки до центра масс сечения. На оси стержня при ρ = 0; напряжение τ = 0; в точках, расположенных в непосредственной близости от поверхности стержня напряжения максимальны. Эпюра изменения τ_ρ вдоль диаметра сечения показана на рис. 5.18, в. Так как величина относительного угла закручивания dφ/dx неизвестна, зависимостью (5.47) для определения касательных напряжений в сечении не пользуются.

Элементарная внутренняя сила, действующая в плоскости сечения на площадку dA с напряжением τ_ρ равна dQ = τ_ρ·dA. Элементарный момент внутренних сил, действующий в плоскости сечения, т.е. элементарный крутящий момент, создаваемый силой dQ относительно центра сечения dT = ρdQ. Сумма этих моментов внутренних сил по всей площади поперечного сечения стержня равна крутящему моменту

.

Так как G = const и dφ/dx = const, то

, (24)

где I_p – полярный момент инерции сечения.

Выразим величину угла закручивания, отнесенного к единице длины стержня

dφ/dx = T/GI_p. (25)

с учетом формулы (25) примет вид

τ_ρ = (T/I_p) ·ρ. (26)

При инженерных расчетах интерес представляют наибольшие напряжения в сечении, т.е. напряжения на поверхности стержня при ρ = d/2,

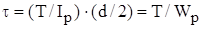, (27)

где W_p = 2I_p/d– полярный момент сопротивления – отношение полярного момента инерции I_p сечения к расстоянию от наиболее удаленной точки сечения до центра масс.

Полярный момент сопротивления для стержня круглого сечения диаметром d равен W_p ≈ 0,2d³, а для стержня кольцевого сечения с внутренним диаметром d ₁ – W_p ≈ [0,2(d³ – d₁⁴/d)].

Условие прочности стержня при кручении с постоянным по длине поперечным сечением имеет вид

τ_max = T_max / W_p ≤ τ_adm, (28)

где Т _max – максимальный крутящий момент по длине деформируемого стержня; τ_adm – допускаемое напряжение при кручении, для стали обычно равно 0,5 … 0,6 допускаемого напряжения σ_adm при растяжении. Предельный из условия прочности крутящий момент определяют по формуле

T_u ≤ W_p·τ_adm, (29)

а минимальный диаметр скручиваемого стержня, учитывая что W_p = = 0,2d³ ≥ T_max/τ_adm равен

d ≥ . (30)

При сравнении стержней, выдерживающих одинаковый крутящий момент, т.е. имеющих поперечное сечение с равным полярным моментом сопротивления W_p, стержень с наименьшей площадью А поперечного сечения будет обладать меньшей массой. Для сравнения различных сечений применяют безразмерную величину, равную отношению W_p / . Чем больше эта величина, тем рациональнее по затратам материала сечение. Так, для швеллера, двутавра она равна 0,04 … 0,07, а для круглого кольца с отношением внутреннего диаметра к внешнему равному 0,9 – она равна 1,16. При кручении рациональным является использование стержней с круглым кольцеобразным сечением.

12	Поделиться:

Воспользуйтесь поиском по сайту: