 |
Понятие скорости волны, ее связь с частотой.
|
|
|
|
Дифракция Фраунгофера на одной щели
Наибольший практический интерес представляют дифракционные явления, наблюдаемые при падении на экран или отверстие в экране параллельного пучка света. В результате дифракции пучок утрачивает параллельность, то есть появляется свет, распространяющийся в направлениях, отличных от первоначального. Распределение его интенсивности на очень большом расстоянии от экрана соответствует дифракции Фраунгофера. Волны, возникающие в результате ограничения падающей плоской волны при прохождении сквозь отверстие на экране, называются дифрагировавшими, а нормали к их волновым поверхностям – дифрагировавшими лучами.
Дифрагировавшие лучи не существуют в рамках геометрической оптики. Возникновение дифрагировавших волн при прохождении через отверстие означает, что волна с ограниченной площадью поперечного сечения не может быть строго плоской.
Рис. 3.17
|
Рассмотрим дифракцию Фраунгофера на одной щели. Пусть на бесконечно длинную щель падает плоская световая волна (рис. 3.17). Поместим за щелью собирающую линзу, а в фокальной плоскости линзы – экран. Фронт падающей волны, плоскость щели и экран параллельны друг другу.
Распределение интенсивности света при дифракции Фраунгофера можно найти с помощью принципа Гюйгенса–Френеля. Интенсивность в точке экрана Р обусловлена интерференцией вторичных волн, исходящих от всех элементарных участков щели. Причем эти волны распространяются в одном и том же направлении, характеризуемом углом j. Заметную интенсивность имеют при этом лишь волны, дифрагировавшие на малые углы.
Когда размеры отверстия велики по сравнению с длиной волны, напряженность поля на поверхности, совпадающей с плоскостью щели, можно считать такой же, какой она была в отсутствии экрана.
|
|
|
Разобьем открытую часть волновой поверхности на параллельные краям щели элементарные зоны шириной 
. Каждая такая зона становится источником вторичных волн. Вторичные волны, посылаемые этими зонами в направлении, определяемом углом j, соберутся в точке экрана Р. Каждая волна, испущенная элементарной зоной, создаст в точке Р колебание 
. Линза собирает в фокальной плоскости плоские волны. Поэтому амплитуда волны 
не зависит от расстояния до точки наблюдения. Ограничившись рассмотрением малых углов j, можно считать, что коэффициент 
. Тогда амплитуда колебания, возбуждаемого зоной в любой точке экрана, будет зависеть только от площади зоны. Площадь зоны пропорциональна ее ширине . Следовательно, колебания от каждой полоски имеют одинаковую амплитуду и отстают по фазе от колебания, создаваемого соседней полоской на одну и ту же величину 
, зависящую от угла дифракции 
.
Чтобы найти значение , проведем плоскость АВ, перпендикулярную к направлению дифрагировавших лучей (рис. 3.18). Собирающая линза обладает свойством, называемым таутохронностью: если свет по двум разным путям распространяется за одно и то же время, то пути называются таутохронными, то есть оптические длины этих путей равны между собой. Условию таутохронизма удовлетворяют все пути лучей, проходящих через линзу. Следовательно, линза не вносит дополнительной разности хода для дифрагировавших волн. Таким образом, достаточно определить разность хода 
, возникающую на пути от плоскости щели до плоскости АВ. Величина связана с разностью хода соотношением 
. Тогда, как видно из рис. 3.18, 
.
Понятие скорости волны, ее связь с частотой.
Итак, в результате суперпозиции нескольких синусоидальных волн образуется несинусоидальная волна с каким-то набором частот и волновых чисел. За скорость распространения такой волны в пространстве берётся скорость распространения фиксированной амплитуды. Но если в случае простой синусоидальной волны эта скорость совпадает со скоростью распространения фиксированной фазы (мы назвали эту скорость фазовой), то в случае сложной несинусоидальной волны сама амплитуда зависит от времени и координат (см. предыдущий пример). Амплитуда сложной волны есть:
|
|
|
Фиксированная амплитуда А будет удовлетворять условию: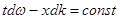 
Взяв полный дифференциал от этого выражения, получим (независимые координаты у нас x и t): 
Скорость распространения фиксированной амплитуды в несинусоидальной волне получается следующей:
Эта скорость называется ГРУППОВОЙ СКОРОСТЬЮ волны. Она в общем случае отличается от фазовой скорости n:
Связь между этими скоростями можно легко получить (учтя зависимость частоты и волнового числа от длины волны):
Среда называется ДИСПЕРГИРУЮЩЕЙ, если в ней волны разной длины распространяются с разной скоростью. Зависимость скорости волны (фазовой) от длины волны (или, что то же самое, от частоты) называется ДИСПЕРСИЕЙ.
Видно, что групповая скорость будет совпадать с фазовой только в недиспергирующих средах, где составляющие сложной волны будут перемещаться с одинаковой скоростью, и сама сложная волна не будет менять своей формы (не будет "расплываться").
Для МОНОХРОМАТИЧЕСКОЙ ВОЛНЫ (так называется простая синусоидальная волна, имеющая одну частоту) фазовая и групповая скорости всегда совпадают, даже в диспергирующих средах.
Фазовая скорость есть чисто абстрактное математическое понятие, эта скорость не связана с перемещением в пространстве чего-либо материального.
Групповая скорость связана с перемещением в пространстве возмущения фиксированной амплитуды; поскольку энергия волны связана с её амплитудой, групповая скорость есть скорость распространения энергии в пространстве.
В общем случае фазовая скорость может превышать скорость света (в случае, например, электромагнитной волны, или волн Де Бройля). Групповая же скорость, в полном согласии с теорией относительности, всегда меньше либо равна скорости света.
|
|
|
Поляризация света.
ПОЛЯРИЗАЦИЯ СВЕТА, упорядоченность в ориентации вектора напряженности электрического E и магнитного H полей световой волны в плоскости, перпендикулярной распространению света. Различают линейную поляризацию света, когда E сохраняет постоянные направления (плоскость, в которой лежит E и световой луч, называется плоскостью поляризации), эллиптическую, при которой конец E описывает эллипс, и круговую (конец E описывает круг). Обычный (естественный) свет не поляризован. Поляризация света возникает при отражении, преломлении света, прохождении через анизотропную среду. Первые указания на поперечную анизотропию светового луча получены Х. Гюйгенсом в 1690; понятие "поляризация света" было введено И. Ньютоном в 1705, а объяснена поляризация света электромагнитной теорией света Дж.К. Максвелла. Поляризованный свет широко используется во многих областях техники (например, для плавной регулировки света, при исследовании упругих напряжений и т.д.). Человеческий глаз не различает поляризацию света, а глаза некоторых насекомых, например пчел, воспринимают ее.
|
|
|
