 |
Методические указания к практическим занятиям
|
|
|
|
Саратовский государственный технический университет
МОДЕЛИ ЛИНЕЙНЫХ
ОДНОМЕРНЫХ И МНОГОМЕРНЫХ
ДИНАМИЧЕСКИХ СИСТЕМ
Методические указания к практическим занятиям
по дисциплине «Основы аналитической теории анализа и синтеза САУ»
для студентов специальности 210100 и направления 550200
Одобрено
редакционно-издательским советом
Саратовского государственного
технического университета
Саратов 2006
ВВЕДЕНИЕ
В управляемых системах используют различные формы представления математических моделей непрерывных динамических систем как одномерных, так и многомерных. Это представление моделей в виде передаточных функций и матриц, в виде дифференциальных уравнений, в форме Коши. Рассматриваются способы перехода от одной формы представления модели к другой.
Практические занятия имеют своей целью систематизацию, закрепление, расширение теоретических знаний и получение практических навыков при решении конкретных технических задач: развитие навыков самостоятельной работы с технической литературой в ходе расчета.
Задачи, рассматриваемые в методических указаниях, соответствуют рекомендациям программы изучения дисциплины, призваны способствовать лучшему усвоению теоретического материала, изучаемого в соответствующем разделе.
ФОРМЫ ПРЕДСТАВЛЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ОДНОМЕРНЫХ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ
ДИНАМИЧЕСКИХ СИСТЕМ
Основные формы представления математических моделей одномерных систем: дифференциальное уравнение, передаточная функция, форма Коши.
Математическая модель в форме дифференциального уравнения имеет вид:
|
|
|
 , (1)
, (1)
где  –
–  -я и
-я и  -я производные по времени от
-я производные по времени от 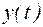 и
и  соответственно.
соответственно.
Операторная (символическая) форма записи дифференциального уравнения:
 ,
,
где  – оператор дифференцирования.
– оператор дифференцирования.
Математическая модель в форме передаточной функции:
 , (2)
, (2)
где  – оператор Лапласа,
– оператор Лапласа,  – комплексная переменная.
– комплексная переменная.
Математическая модель в форме Коши:
 (3)
(3)
где  –
– 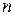 -мерный вектор состояний;
-мерный вектор состояний; 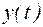 – выходная переменная;
– выходная переменная;  – входная переменная (управление);
– входная переменная (управление);  – матрицы чисел размерами
– матрицы чисел размерами  соответственно;
соответственно;  – число.
– число.
ФОРМЫ ПРЕДСТАВЛЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ОДНОМЕРНЫХ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ
ДИНАМИЧЕСКИХ СИСТЕМ
Формы представления математических моделей многомерных систем: форма Коши, форма «вход-выход», передаточная матрица.
Модель многомерной системы в форме Коши имеет вид:
 , (4)
, (4)
 , (5)
, (5)
где  –
–  -мерный вектор состояний;
-мерный вектор состояний;  –
–  -мерный вектор выходных переменных;
-мерный вектор выходных переменных;  –
– 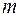 -мерный вектор входных переменных (управлений);
-мерный вектор входных переменных (управлений); 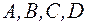 – матрицы размеров
– матрицы размеров  соответственно.
соответственно.
Векторно-матричное дифференциальное уравнение (4) называется уравнением состояний, а векторно-матричное алгебраическое уравнение (5) – уравнением выходов.
Математическая модель в виде передаточной матрицы.
Передаточная матрица связывает изображение Лапласа вектора выходных переменных  с изображением Лапласа вектора входных переменных
с изображением Лапласа вектора входных переменных  и имеет вид:
и имеет вид:
 . (6)
. (6)
Уравнение в форме «вход-выход»:
 , (7)
, (7)
где  ,
,  – полиномиальные матрицы.
– полиномиальные матрицы.
Пример 1. Для электрической схемы (рис.1) составить математическую модель: а) в виде дифференциального уравнения; б) в виде передаточной функции; в) в виде уравнений в форме Коши.

Рис.1
Замечание. В качестве входного (управляющего) воздействия принять  , в качестве выходного –
, в качестве выходного –  .
.
Решение.
а) Из закона Кирхгофа 
и выражений 
получаем математическую модель в виде дифференциального уравнения:
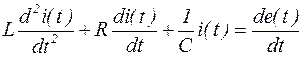 . (8)
. (8)
Операторный вид уравнения (8)
 .
.
б) Математическая модель в виде передаточной функции получается путем применения оператора Лапласа к обеим частям дифференциального уравнения (8) при нулевых начальных значениях функций и их производных:
|
|
|
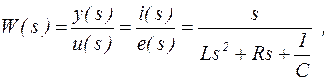
где 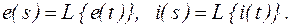
в) Введем обозначения:
 (9)
(9)
Продифференцируем (9) по времени:
 (10)
(10)
Из первого уравнения (10) и выражения (8) следует, что  .
.
Из второго уравнения (10) и первого уравнения (9) получаем:
 .
.
Выразим  из второго уравнения (9):
из второго уравнения (9):  , (11)
, (11)
и подставим в выражения для  и
и 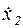 :
:
 (12)
(12)
Уравнения (11), (12) в векторно-матричной форме имеют вид (3):

где 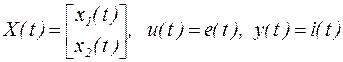 , а матрицы A, B, C, D имеют вид:
, а матрицы A, B, C, D имеют вид:
 .
.
Пример 2. Для электрической схемы (рис. 2): а) построить математическую модель в форме Коши; б) получить передаточную матрицу, связывающую изображения входных переменных  (
( – напряжения источников) и изображения выходных переменных
– напряжения источников) и изображения выходных переменных 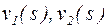 (
( – напряжения на сопротивлениях
– напряжения на сопротивлениях  и
и 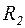 ).
).

Рис. 2
Решение.
а) По закону Кирхгофа для узла 1 имеем:
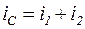 или
или  . (13)
. (13)
Рассмотрим контуры I и II. По закону Кирхгофа для напряжений получаем:
 , (14)
, (14)
 . (15)
. (15)
Введем обозначения: 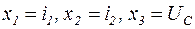 .
.
Тогда выражения (13), (14), (15) можно записать в виде:
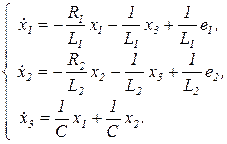 (16)
(16)
Уравнения для выходных переменных:
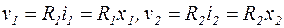 . (17)
. (17)
Объединив уравнения (16), (17), получаем математическую модель электрической схемы в форме Коши (выражения (4), (5)):
где  ,
,
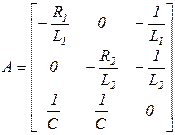 ,
, 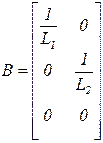 ,
,  ,
,  .
.
Подставив числовые значения параметров (рис. 2), получим:
 .
.
б) Так как  , то
, то 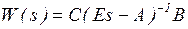 .
.
 ,
,
 .
.
Тогда
 .
.
Окончательно выражение для математической модели в виде передаточной матрицы будет иметь следующий вид:
 .
.
Зная передаточную матрицу, можно записать дифференциальные уравнения, связывающие выходные и входные переменные. Из выражения для  следует:
следует:

Переходя к оригиналам, получим:

или 
Пример 3. Дана математическая модель системы в виде дифференциального уравнения 3-го порядка:
 . (18)
. (18)
Получить математическую модель системы в форме Коши двумя способами (в формах Крылова – Люенбергера и Фробениуса).
Решение.
Способ 1. Введем переменные  ,
, 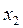 ,
,  следующим образом:
следующим образом:
 (19)
(19)
Продифференцируем систему уравнений (19) по времени:
 (20)
(20)
Сопоставляя первое уравнение (20) с выражением (18), второе уравнение (20) с первым уравнением (19), третье уравнение (20) со вторым уравнением (19), получим:
 (21)
(21)
Из третьего уравнения (19) выразим:  , (22)
, (22)
и подставим в (21):
 (23)
(23)
Введем в (22), (23) обозначения:
 .
.
Совокупность уравнений (22), (23) и есть математическая модель системы в форме Коши (3) (форма Крылова–Люенбергера).
|
|
|
Способ 2. Запишем уравнение (18) в операторном виде:
 . 24)
. 24)
Выражение (24) можно переписать следующим образом:
 , (25)
, (25)
откуда  , (26)
, (26)
 . (27)
. (27)
Введем обозначения:  . (28)
. (28)
С учетом (28) соотношение (27) можно переписать в виде:
 ,
,
или  . (29)
. (29)
Так как  , то из (29) следует, что
, то из (29) следует, что
 . (30)
. (30)
Окончательно получим, объединив (26), (28), (30):
 (31)
(31)
Вводя обозначения
 ,
, 
получаем математическую модель системы в форме Коши (3) (форма Фробениуса).
Замечание. Приведенные алгоритмы перехода к форме Коши можно распространить на модели систем в виде дифференциальных уравнений произвольного порядка.
Пример 4. Задана математическая модель системы в виде дифференциального уравнения без производных в правой части:
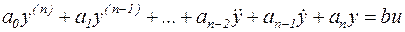 . (32)
. (32)
Получить математическую модель системы в форме Коши.
Решение.
Введём переменные  следующим образом:
следующим образом:
 . (33)
. (33)
Из выражений (32), (33) следует:
 (34)
(34)
С учетом (33) выражения (34) примут вид:
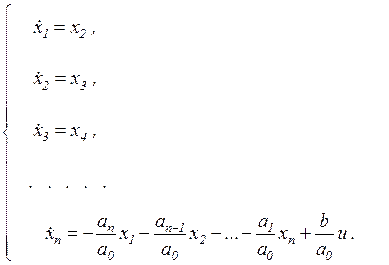 (35)
(35)
Добавив к (35) уравнение выхода 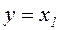 , (36)
, (36)
получим математическую модель в форме Коши, то есть в виде (3), где обозначено

 .
.
Пример 5. Для электрической схемы (рис. 3):
а) составить математическую модель в форме Коши;
б) построить выражение для математической модели в виде передаточной матрицы, связывающей изображения входных переменных  и выходных переменных
и выходных переменных  ;
;
в) определить матрицу  , элементами которой являются импульсные переходные характеристики
, элементами которой являются импульсные переходные характеристики  для
для  -го выхода относительно
-го выхода относительно  -го входа (при нулевых состояниях на всех остальных входах).
-го входа (при нулевых состояниях на всех остальных входах).

Рис. 3
Решение.
а) По аналогии с примером 2 уравнения электрической схемы можно получить в виде:
 ,
, 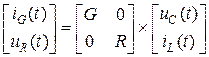 .
.
Эти уравнения записаны в форме Коши (4), (5).
При  Ф,
Ф, 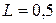 Гн,
Гн,  [1/Ом],
[1/Ом],  Ом соответствующие матрицы получают следующие численные значения:
Ом соответствующие матрицы получают следующие численные значения:
 .
.
б) Аналогично примеру 2 находим:
 ,
,
 .
.
Тогда выражение для математической модели в виде передаточной матрицы принимает вид:
 ,
,
или  .
.
Таким образом,
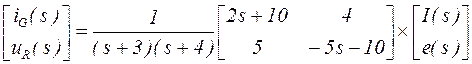 .
.
в) Так как изображение  -й выходной переменной
-й выходной переменной
 ,
,
то элементы  матрицы
матрицы  можно рассматривать как скалярные передаточные функции от
можно рассматривать как скалярные передаточные функции от  -го входа к
-го входа к  -му выходу, причем
-му выходу, причем
|
|
|
 при
при  .
.
Зная 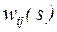 , можно получить импульсные переходные характеристики
, можно получить импульсные переходные характеристики  . Переходя в выражении
. Переходя в выражении  к оригиналам, получим:
к оригиналам, получим:
 .
.
ЗАДАЧИ ДЛЯ УПРАЖНЕНИЙ
1. Задана математическая модель системы в виде дифференциального уравнения (табл. 1). Требуется:
а) записать математическую модель системы в форме Коши двумя способами (в формах Фробениуса и Крылова–Люенбергера);
б) записать математическую модель системы в виде передаточной функции;
в) с помощью функций tf и ss системы МАТЛАБ получить модель в переменных состояния (форма Коши).
Таблица 1
| Номер варианта | Дифференциальное уравнение |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |
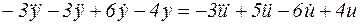
| |

| |

| |
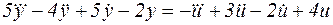
| |

| |

| |

| |

| |
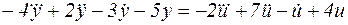
| |

| |
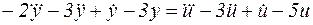
| |

| |
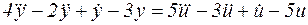
|
2. Выполнить задания примера 2 для числовых данных, заданных в табл. 2.
Таблица 2
| Номер варианта | Значения параметров | ||||
 ,
Ом ,
Ом
| 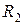 ,
Ом ,
Ом
|  ,
Гн ,
Гн
| 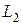 ,
Гн ,
Гн
|  ,
Ф ,
Ф
| |
| 0,2 | |||||
| 0,5 | 0,5 | 0,2 | |||
| 0,5 | 0,5 | 0,5 | |||
| 0,5 | 0,5 | ||||
| 0,5 | 0,5 | ||||
| 0,5 | 0,4 | 0,5 | |||
| 0,4 | 0,5 | 0,2 | |||
| 0,5 | 0,5 | 0,5 | 0,25 | ||
| 0,5 | 0,5 | 0,25 | |||
| 0,2 | |||||
| 0,5 | |||||
| 1,5 | |||||
| 1,5 | 0,4 | ||||
| 0,5 | |||||
| 0,1 | |||||
| 0,02 | |||||
| 0,02 | |||||
| 0,04 | |||||
| 0,04 | |||||
| 0,05 | |||||
| 0,05 | |||||
| 0,1 | |||||
| 0,1 | |||||
| 0,2 | |||||
| 0,5 |
3. Для числовых данных примера 2 (табл. 2) с помощью функций ss и tf системы МАТЛАБ получить модель в виде передаточной функции.
4. Выполнить задания примера 5 для числовых данных, заданных в табл. 3.
. Таблица 3
| Номер варианта | Значения параметров | |||
 ,
Ом ,
Ом
|  ,
1/Ом ,
1/Ом
|  ,
Гн ,
Гн
|  ,
Ф ,
Ф
| |
| 0,2 | ||||
| 0,5 | 0,2 | |||
| 0,5 | 0,5 | |||
| 0,5 | 0,5 | |||
| 0,5 | ||||
| 0,5 | 0,5 | |||
| 0,4 | 0,2 | |||
| 0,5 | 0,5 | 0,25 | ||
| 0,5 | 0,25 | |||
| 0,2 | ||||
| 0,5 | ||||
| 1,5 | 0,4 | |||
| 0,5 | ||||
| 0,1 | ||||
| 0,2 | ||||
| 0,2 | ||||
| 0,3 | ||||
| 0,3 | ||||
| 0,2 | ||||
| 0,5 | ||||
| 0,1 | ||||
| 0,2 | ||||
| 0,1 | ||||
| 0,5 |
5. Задана математическая модель системы в виде передаточной функции, где u(t) – входная переменная, y(t) – выходная переменная:
а)  ;
;
|
|
|
б)  ;
;
в)  ;
;
г) 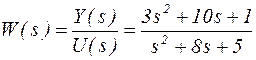 ;
;
д) 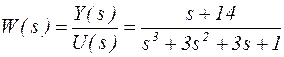 .
.
Записать модель системы в виде дифференциального уравнения.
Получить математическую модель системы в виде формы Коши:
1) используя результаты примера 3 (формы Фробениуса и Крылова– Люенбергера);
2) при помощи функций tf и ss системы МАТЛАБ;
Сравнить результаты п.п. 1, 2 и прокомментировать их.
6. Задана математическая модель системы в виде уравнений состояний и выходов (форма Коши). Получить математическую модель системы в виде передаточной функции при помощи команд tf и ss системы МАТЛАБ:
а)  ,
,  ;
;
б)  ,
, 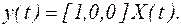
7. С помощью функций ss и tf системы МАТЛАБ определить передаточные функции для систем, модели которых в переменных состояния представлены следующими матрицами:
а) 
б) 
в)  .
.
8. Рассмотрите две математические модели системы в форме Коши:
а) 

и
б) 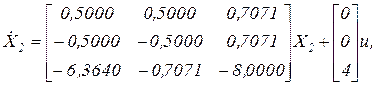
 .
.
1) С помощью функций tf и ss системы МАТЛАБ определить математическую модель системы в форме передаточной функции y(s) / u(s) для системы а).
2) С помощью функций tf и ss системы МАТЛАБ определить математическую модель системы в форме передаточной функции y(s) / u(s) для системы б).
3) Для передаточных функций систем, полученных в п.п. 1, 2 с помощью функций tf и ss системы МАТЛАБ определить математические модели систем в форме Коши.
4) Сравнить результаты п.п. 1, 2, 3 и прокомментировать их.
ЛИТЕРАТУРА
ОСНОВНАЯ
1. Дерусоо Г. Пространство состояний в теории управления /
Г. Дерусоо, Р. Рой, Ч. Клоуз. – М.: Наука, 1970.
2. Директор Р. Введение в теорию систем / Р. Директор, С. Рорер. – М.: Высшая школа, 1971.
3. Сигорский В.П. Математический аппарат инженера /
В.П. Сигорский. – Киев: Техника, 1977.
4. Подчукаев В.А. Теория автоматического управления /
В.А. Подчукаев. – М.: Физматлит, 2005.
5. Теория автоматического управления: в 2 ч. / под ред. А.А. Воронова. – М.: Высшая школа, 1986.
ДОПОЛНИТЕЛЬНАЯ
1. Бесекерский В.А. Теория систем автоматического регулирования / В.А. Бесекерский, Е.П. Попов. – М.: Наука, 1975.
2. Дорф Р. Современные системы управления / Р. Дорф, Р. Бишоп. – М.: Лаборатория базовых знаний, 2002.
3. Математические основы теории автоматического регулирования / под ред. В.К. Чемоданова. – М.: Высшая школа, 1977.
4. Теория автоматического управления: в 2 ч. / под ред.
А.В. Нетушила. – М.: Высшая школа, 1976, 1983.
5. Ту Ю. Современная теория управления / Ю. Ту. – М.: Машиностроение, 1971.
МОДЕЛИ ЛИНЕЙНЫХ
ОДНОМЕРНЫХ И МНОГОМЕРНЫХ
ДИНАМИЧЕСКИХ СИСТЕМ
Методические указания к практическим занятиям
по дисциплине «Основы аналитической теории анализа и синтеза САУ»
| Составили: | ЕФИМОВ Роман Павлович ТИМОФЕЕВ Юрий Константинович ТОРГАШОВА Ольга Юрьевна |
| Рецензент С.А. Моисеенко | |
| Редактор О.А. Луконина |
Подписано в печать 20.12.06 Формат 60x84 1/16
Бум. тип. Усл. печ.л. 1,16 (1,25) Уч.-изд.л. 1,1
Тираж 100 экз. Заказ Бесплатно
Саратовский государственный технический университет
410054, Саратов, Политехническая ул. 77
Отпечатано в РИЦ СГТУ. 410054, Саратов, Политехническая ул. 77
|
|
|


