Формирование стрелы времени

Теперь нужно ответить на самый главный и интригующий вопрос, касающийся времени – это вопрос об не обратимости времени.

Мы уже отмечали, что события наступают в результате протекания тех или иных процессов. Даже само событие есть какой-то процесс со своей динамикой, со своими энерго превращениями. Поэтому что бы ответить на вопрос о возможности или не возможности обратной цепи событий, обратного хода времени, нужно ответить на вопрос о возможности или невозможности обратного течения процессов. Вопрос обратимости или не обратимости времени – это вопрос обратимости или не обратимости процессов в динамике. Последнее проходит красной линией в исследованиях Пригожина и его коллег по данному вопросу. (См. например, [Л-15, 16]).

Сначала о обратимости процессов в динамике Ньютона, динамике малого, счётного числа взаимодействующих частиц.

Рассмотрим один из наиболее ярких примеров обратимости процессов в динамике Ньютона – это обратимость движения математического маятника. При качании маятника в ту или иную сторону движения строго повторяются и при описании движения время можно принимать как со знаком плюс так и со знаком минус. Ни с точки зрения количества, ни с точки зрения качества оба описания не будут противоречить друг другу. Качание в одну сторону строго противоположно, обратимо качанию в другую сторону. Усложним ситуацию. Рассмотрим цепочку подвешенных на прямой линии достаточно близко друг к другу совершенно одинаковых математических маятников. Отклоним первый маятник, то есть за счёт совершения работы передадим ему потенциальную энергию, и отпустим. Взаимодействие будем описывать законами центрального абсолютно упругого удара. В системе начнётся процесс последовательного соударения и в цепочке возникнет процесс передачи импульса и энергии вдоль цепочки. При этом каждый акт взаимодействия между массами двух маятников сопровождается переходом кинетической энергии в потенциальную и наоборот и совершается работа против силы или силой. Этот процесс будет протекать до последнего маятника. После того как последний маятник отклонится и энергия системы сосредоточится в потенциальной энергии последнего маятника, весь процесс повторится, но в обратной последовательности, в обратном направлении. Мы растянули процесс во времени, но он остался обратимым. Однако если цепочку маятников предположить бесконечной длины, то процесс передачи импульса и энергии по цепочке станет необратимым. Таким образом теоретически необратимость процесса возможна и в классической динамике Ньютона, но это не локализованная в пространстве и во времени, гипотетическая необратимость, за счёт несчётного числа маятников.

Теперь о необратимости процессов в термодинамике, динамике большого, несчётного числа частиц, которая, как показывает практика, локализована и во времени и в пространстве.

Исторически сложилось так, что при рассмотрении процессов в неравновесных термодинамических системах в тени остаётся один из самых фундаментальных законов природы – закон сохранения результирующего импульса. В основу термодинамики был положен факт существования равновесного состояния в тепловых системах и неизбежности его наступления. Были сформулированы нулевой и второй постулаты, которые напрочь заслонили закон сохранения результирующего импульса как системный закон в применении к системам из несчётного числа частиц.

Во первых покажем что результирующий импульс всех частиц системы, находящейся в равновесии, равен нулю как вектор.

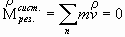где n-количество частиц в системе.

Обоснование данного утверждения легко провести с помощью выводов статистической физики. Известно, что в случае равновесного состояния в газе всегда реализуется Максвеловское распределение по скоростям. В статистической физике показывается, что для случая Максвеловского распределения по скоростям средняя проекция скорости хаотического движения на любое направление оказывается равной нулю. А если равна нулю проекция средней скорости, то равна нулю и проекция среднего импульса на любое направление. И результирующий импульс равен нулю как вектор.

На основе последовательного применения к термодинамическим системам (системам состоящим из несчётного числа частиц) закона сохранения результирующего импульса покажем единство динамики малого числа частиц (динамики Ньютона) и динамики несчётного числа частиц (термодинамики).

Наиболее характерным свойством замкнутой системы, с точки зрения динамики Ньютона, будет, наряду с сохранением полной энергии то, что результирующий импульс сохраняется постоянным по величине и направлению, сколько бы частицы не сталкивались между собой, какие бы события не развивались в системе. Однако положение коренным образом меняется при рассмотрении замкнутой системы из многих и многих миллиардов частиц. Наиболее характерным свойством этой системы является стремление к равновесию, при котором как было показано выше результирующий импульс всех молекул равен нулю как вектор, т.е. направленное движение переходит в хаотическое. 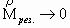Таким образом с одной стороны для замкнутой механической системы имеем с другой, при увеличении числа частиц системы, имеем прямо противоположное свойство , направленное движение исчезает. Попытаемся выяснить, каким образом разрешается этот парадокс. Взаимодействие молекул (шаров) будем описывать в соответствии с законами сохранения энергии и импульса. Так как молекулы имеют конечные размеры, то удар будет нецентральный. Обратим на это особое внимание. Это ключ к решению поставленной задачи. Под молекулами (шарами) будем понимать силовые поля, имеющие форму шара или круговые эффективные сечения взаимодействия. Причём шаровые силовые поля рассматриваем для упрощения модели, что бы заострить внимание на главном виновнике рассеяния кооперативной энергии – нецентральном соударении.

Рассмотрим многочастичную замкнутую равновесную механическую систему, которой одноактно передан некоторый импульс. Этот импульс будет для данной системы оставаться постоянным по величине и по направлению какие бы события не развивались в данной системе. Пусть события в системе после передачи импульса развиваются таким образом, что масса результирующего импульса постоянно растёт. При этом скорость результирующего импульса должна соответственно уменьшаться (см. (4)), и кинетическая энергия, связанная с результирующим импульсом уменьшается обратно пропорционально росту массы (см.(5) и (7)). И если масса результирующего импульса в (4) становится сколь угодно большой, то кинетическая энергия (5) становится сколь угодно малой. Кинетическая энергия, связанная с результирующим импульсом, исчезает.

Это видно и из таких простых математических преобразований:

; (4) ; (5)

; m-масса шара; (6) ; (7)

Рассмотрим события и механизмы, приводящие к реализации выше сказанного. Что приводит к росту массы результирующего импульса и куда девается кинетическая энергия? Пусть имеем замкнутую систему, состоящую из одинаковых шаров. Причем n шаров покоятся, а один шар движется и сталкивается с покоящимися шарами. До столкновения результирующий импульс системы: , т.е. равен импульсу движущегося шара, а кинетическая энергия равна кинетической энергии движущегося шара. Причем кинетическая энергия строго направлена по результирующему импульсу системы, вся переносима этим результирующим импульсом.

Шар 1 (см. Рис.1) сталкивается с покоящимися шарами, причем должны при этом выполняться закон сохранения результирующего импульса и закон сохранения кинетической энергии. Пишу закон сохранения кинетической, а не полной энергии, т.к. принято считать, что при абсолютно-упругом соударении шаров потенциальная энергия проявляется только в момент непосредственного соприкосновения. Эта схема принимается мною с тем, что бы в наибольшей простоте раскрыть механизм рассеяния кооперативной кинетической энергии. При рассмотрении последовательности столкновений будем следить не за траекториями отдельных частиц, которые экспоненциально разбегаются, а за поведением результирующего импульса.

Шар 1 с импульсом после столкновения с первым покоящимся шаром 2 будет иметь импульс , а шар 2 приобретет импульс которые в сумме (геометрической) дадут первоначальный импульс . Закон сохранения импульса соблюден. Разложим импульсы шаров 1 и 2 после столкновения на оси и . Проекции и 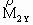дадут в сумме первоначальный импульс , а проекции , перпендикулярные первоначальному результирующему импульсу на его величину после столкновения не влияют и в сумме дают нуль-вектор. Равенство по абсолютной величине импульсов и легко видно из векторной диаграммы и вытекает из закона сохранения результирующего импульса. Однако эти два последних уравновешенных импульса (нуль-вектор) несут каждый на себе определенное количество кинетической энергии, полученной от кинетической энергии первоначального импульса .

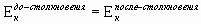
Так как 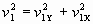и

Рис. 1

Массы шаров для простоты все равны. Если, как было показано выше, результирующий импульс после столкновения сложится из двух проекций на ось и остался постоянным, то кинетическая энергия, переносимая этим импульсом после столкновения, т.е. проекциями и 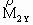будет составлять только часть кинетической энергии, переносимой результирующим импульсом до столкновения. Другая часть кинетической энергии, переносимая взаимно уравновешенными импульсами и (нуль-вектором) переходит в хаотическую форму. После следующего соударения теперь уже двух движущихся шаров результирующий импульс сложится из 4-х шаров и произойдет дополнительное рассеяние направленной кинетической энергии и т.д. Таким образом благодаря нецентральному соударению шаров в первоначальный направленный импульс лавинообразно вовлекается все большее и большее число шаров и происходит лавинообразный рост массы результирующего импульса. А по мере вовлечения шаров происходит все большее рассеяние первоначально направленной кинетической энергии. Речь идет о кинетической энергии общего переноса (кооперативной энергии), связанной с результирующим импульсом, т.е. той энергии, которая совершает макроскопическую работу. Закон сохранения общей кинетической энергии системы не нарушается, т.к. адекватно увеличивается хаотическая составляющая кинетической энергии, связанной с нуль-вектором. При увеличении массы, переносящей результирующий импульс, кинетическая энергия, переносимая этим импульсом, и остающаяся в направленной форме, уменьшается обратно пропорционально росту массы. И при стремлении массы результирующего импульса к бесконечности кинетическая энергия общего переноса стремится к нулю. Результирующий импульс, оставаясь постоянным по величине и направлению, вырождается как носитель кооперативной энергии, равносильно тому, что и система приходит в равновесное состояние. Вся кооперативная энергия переходит к нуль-вектору хаоса.

Этим разрешается парадокс, который мы отметили в начале. Применяя закон сохранения импульса к диссипативным системам необходимо учитывать одну тонкость, которая и позволяет снять ранее отмеченное противоречие и примирить 2-й закон и закон сохранения результирующего импульса. Эта тонкость является важным свойством диссипативных (термодинамических) систем. Под скоростью центра масс результирующего импульса (см. формулу (7)) нужно понимать не скорость центра масс всей замкнутой системы, которой передан импульс, а скорость центра масс частиц вовлечённых в результате не центрального соударения в перенос первоначального импульса (который относился к первоначальному шару). Это открытая подсистема, активно взаимодействующая с остальной несоизмеримо большей частью всей замкнутой системы и вовлекающая в первоначальный импульс всё большее число молекул через не центральное соударение. Учитывая число частиц реальных термодинамических систем (достаточно вспомнить порядок числа Лошмидта), понятно, что в доли времени и на минимальных расстояниях первоначальная масса частиц, из которых складывался импульс, возрастает на многие и многие порядки раз. Хотя первоначальный импульс остался постоянным по величине и направлению как вектор (сложившись из огромного числа микро импульсов вовлеченных частиц), он вырождается как носитель кооперативной энергии, которая перешла к нуль-вектору, складывающемуся из пар взаимно уравновешенных импульсов. Так как скорость центра масс открытой системы стремится к нулю (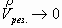), то я и утверждаю, что с продолжающимся лавинообразным нарастанием массы открытой системы с некоторого момента следующий миллиметр пути импульс не преодолеет никогда, а это значит, что перенос кооперативной энергии прекратится. Оставаясь постоянным по величине и направлению как вектор, импульса не стало как энергетического носителя кооперативной энергии. Вот что я понимаю под вырождением результирующего импульса. Он остался постоянным по величине и направлению, но без энергии. Вся его первоначальная энергия перешла к нуль вектору хаоса. Именно это я имею в виду когда пишу . Это и есть механизм рассеяния, механизм необратимости через диссипацию кооперативной энергии, через вырождение результирующего импульса при не центральном соударении. Более подробно об механизме эффекта вырождения результирующего импульса в многочастичной среде можно ознакомиться в [Л-6, 7, 9].

Всесилие механизма рассеяния, приводящего систему к равновесию, заключается в том, что материя имеет корпускулярное строение, т.е. частицы имеют конечные размеры, а значит соударение нецентральное. Частиц же великое множество и затухание происходит очень быстро. Именно благодаря этому простому, но всесильному механизму обратимые законы механики в приложении к многомолекулярным системам, вырождаются в необратимые законы статистики. Ведь для обращения процесса рассеяния назад необходимо, чтобы в один и тот же момент все частицы системы, вовлеченные так или иначе в процесс рассеяния, столкнулись по закону центрального абсолютно-упругого удара с каким-то препятствием, чтобы отлететь с той же скоростью в строго обратном направлении. Это невозможно в принципе. Во - первых в реальности не возможен абсолютно-упругий удар. Во - вторых как в многомолекулярной системе вообще организовать внедрение этих очень массивных, теоретически с бесконечной массой, препятствий? Причём бесконечные массы перед каждой из частиц нужно внедрить мгновенно, в один момент, и при этом обеспечить строго центральное соударение, чтобы все частицы одновременно повернуть назад. Как это сделать, учитывая порядок числа Лошмидта и то, что реальные частицы не шары? Сказанное и является основой необратимости процесса вырождения импульса в термодинамических системах. Релаксация и необратимость вытекают из обратимых законов механики при их действии в среде многомолекулярных систем. Обратим особое внимание на это свойство диссипативных сред, их способность качественно вырождать закон сохранения результирующего импульса и как следствие качественно изменять динамику, когда детерминизм динамики уступает место вероятности статистической механики. Это происходит в результате действия эффекта вырождения результирующего импульса, который является стержневым свойством многочастичных (диссипативных) сред. Именно принципиальная необратимость эффекта вырождения результирующего импульса в многочастичных системах приводит к необратимости макроскопических процессов, следствием чего является необратимая последовательность событий, наличие стрелы времени. Принципиальная схема эволюции, приводящая к понятию стрелы времени, изображена на рисунке 2.

“Историческое развитие физических представлений о пространстве и времени происходило по двум направлениям в тесной связи с различными философскими представлениями. В начале одного из них лежали идеи Демокрита, приписывающего пустоте особый род бытия. Они нашли наиболее полное физическое воплощение в ньютоновских понятиях абсолютного пространства и абсолютного времени. Согласно И. Ньютону, абсолютные пространство и время представляли собой самостоятельные сущности, которые не зависели ни друг от друга, ни от находящихся в них материальных объектов и протекающих в них процессов. Другое направление развития представлений о пространстве и времени восходит к Аристотелю и было разработано в философских работах немецкого учёного Г.В. Лейбница, трактовавшего пространство и время как определённые типы отношений между объектами и их изменениями, не имеющие самостоятельного существования. В физике концепция Лейбница была развита А. Эйнштейном в теории относительности”. [Л-19]. Развитие первого направления к настоящему времени в своих крайних формах приводит к высказываниям о возможности изменения направления времени и переходе в состояния прошлого или будущего, о возможности взаимопревращений пространства и времени. [см. Л-1, 15, 20]. Автор данной статьи придерживается второго направления. Представление о времени как о понятии вытекающем из наблюдения за скоростями процессов позволило объяснить необратимость эволюционного времени, необратимостью многочастичных процессов.

Необходимо обратить внимание и на такие важнейшие понятия философии и методологии познания как причина и следствие, на их строгую последовательность и предопределённость. Следствием этой строгой последовательности и предопределённости и возникает понятие стрелы времени. Но строгая последовательность и предопределённость причины и следствия существуют только в области протекания необратимых процессов. Если мы вновь вернёмся к классическому обратимому процессу – процессу качания математического маятника, то не сможем отличить причину от следствия. Нельзя с определённостью сказать, что первично: наличие градиента потенциальной энергии в верхних точках равновесия или наличие кинетической энергии в нижней точке. В обратимых процессах причина и следствие постоянно меняются местами. Мир обратимых процессов однообразен и не подвержен эволюционному развитию. В области же необратимых процессов, благодаря необратимости эффекта вырождения импульса причина и следствие различимы в наблюдаемой последовательности событий и явлений.

Рис. 2

Таким образом именно принципиальная необратимость эффекта вырождения результирующего импульса обеспечивает многообразие и эволюционное развитие окружающего нас мира.

Необратимость эволюционного времени обеспечивается корпускулярным характером строения материи, который приводит через нецентральное соударение к эффекту вырождения результирующего импульса. Если принять возможным изменение направления эволюционного времени, то необходимо отказаться от самых фундаментальных постулатов динамики: закона сохранения и превращения энергии, закона сохранения результирующего импульса и корпускулярного характера строения материи, которые в совокупности приводят к эффекту вырождения результирующего импульса в многочастичной среде.

ЗАКЛЮЧЕНИЕ

Времени как некоторой субстанции, как чего-то существующего само по себе нет. Есть процессы, протекающие в физической реальности с присущей им быстротой (скоростью) и череда событий, наступающая как следствие протекающих в физической реальности процессов.

Под стрелой времени понимается необратимая череда эволюционных событий. Необратимость событий обусловлена свойствами материального мира, состоящего из несчётного числа движущихся корпускул конечных размеров. Эти свойства порождают через нецентральное соударение эффект вырождения результирующего импульса, диссипацию кооперативной энергии и принципиальную необратимость процессов в термодинамических (диссипативных, статистических) системах.

Время – это скорость равномерного периодического процесса принятая в качестве эталона сравнения. Направление числовой оси времени связано с необратимостью процессов протекающих в диссипативных средах, как следствие необратимости эффекта вырождения результирующего импульса.

Время это просто введённая наблюдателем интеллектуальная категория, позволяющая оценивать быстроту (скорости) динамических процессов и фиксировать наступление эволюционных событий.

Список литературы

1. Арушанов М.П., Коротаев С.М. Поток времени как физическое явление (по Н.А. Козыреву). http://www.sciteclibrary.ru/rus/catalog/pages/6012.html

2. Базаров И.П. Термодинамика. – г. Москва, из-во “Высшая школа”, 1991г.

3. Власов В.В. Основы векторной энергетики. М.: Буркин. 1999г. – 124с.

4. Гельфер Я.М. История и методология термодинамики и статистической физики. – г. Москва, из-во “Высшая школа”, 1981г.

5. Губский Е.Ф., Кораблёва Г.В., Лутченко В.А. Философский энциклопедический словарь. – М.: ИНФРА-М, 2003г. – 576с.

6. Косарев А.В. Динамика эволюции неравновесных диссипативных сред. – г. Оренбург, ИПК ”Оренбурггазпромпечать”, 2001г. - 144 стр.

7. Косарев А.В. Эффект вырождения результирующего импульса – ключ к пониманию динамики кооперативных потоков. http://www.sciteclibrary.ru/rus/catalog/pages/4231.html

8. Косарев А.В. Стрела времени и необратимость, возникновение хаоса из порядка и порядка из хаоса как следствие фундаментального детерминизма. http://www.sciteclibrary.ru/rus/catalog/pages/5117.html

9. Косарев А.В. Закон роста энтропии как следствие эффекта вырождения результирующего импульса и двойная природа второго закона термодинамики. // Вестник Оренбургского гос. универсттета. – 2003, №7. – с.177-181. http://vestnik.osu.ru/2003_7/39.pdf

10. Косарев А.В. Время в динамике процессов и в эволюции событий. // Доклады 6 Российской научной конференции “Векторная энергетика в технических, биологических и социальных системах”, Балаково, 2003. – с.32-37.

11. Косарев А.В. К статье “Время в динамике процессов и в эволюции событий”. // Доклады 7 Российской научной конференции “Векторная энергетика в технических, биологических и социальных системах”, Балаково, 2004. – с.38-44.

12. Ландау Л.Д., Лифшиц Е.М. Краткий курс теоретической физики. Книга 1. Механика. Электродинамика. – М.: Наука, 1969г. – 272с.

13. Николис Г., Пригожин И. Самоорганизация в неравновесных системах. – г. Москва, из-во “Мир”, 1979г.

14. Осипов А.И. Самоорганизация и хаос. – г. Москва, из-во “Знание”, 1986г.

15. Пригожин И., Стенгерс И. Время, хаос, квант. М.: Прогресс, 1994г. - 272с.

16. Пригожин И. От существующего к возникающему. М.: Наука, 1985г. - 326с.

17. Сивухин Д.В. Общий курс физики. Т-1, Механика. М.: Наука, 1979г. - 520с.

18. Фейнман Р. и др. Фейнмановские лекции по физике. Т-1 и 2. М.: Мир, 1977г. – 440с.

19. Физический энциклопедический словарь. М.: Советская энциклопедия, 1983г. - 945с.

20. Юхимец А.К. Как непротиворечиво понимать время. http://www.sciteclibrary.ru/rus/catalog/pages/7217.html

Для подготовки данной работы были использованы материалы с сайта http://www.sciteclibrary.ru

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: