Пример 10.2. Задача о максимальном потоке

ПОТОКИ В СЕТЯХ

Одной из наиболее важных задач теории графов является задача опре­деления максимального потока, протекающего от некоторой вершины графа s (источника) к вершине t (стоку). Примерами таких задач могут быть: перевозка наибольшего товара, максимальное количество жидко­сти и газа, транспортируемых по трубопроводам, информация по ком­пьютерной и телефонной сети и др.

Потоком в сети G = (Х,U) от входа s к выходу t называется неотрица­тельная функция U, определенная на множестве дуг сети со следующими свойствами:

(10.4)

(10.5)

Условие (10.4) является уравнением сохранения потока, согласно ко­торому поток, втекающий в вершину, равен потоку, вытекающему из нее, за исключением вершин s и t (источник и сток).

Ограничение (10.5) указывает, что пропускные способности дуг огра­ничены для каждой дуги графа G.

Задача состоит в нахождении такого множества потоков по дугам, чтобы

(10.6)

при ограничениях (10.4) и (10.5).

Теорема Форда - Фалкерсона

(о максимальном потоке и минимальном разрезе)

Величина максимального потока из s в t равна значению минималь­ного разреза отделяющего источник s от стока t.

Разрез отделяет s от t, если ,а . Величиной такого разреза называется сумма пропускных способностей всех дуг из G, начальные вершины которых лежат в Хо, а конечные — в , т.е.

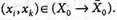
(10.7)

Минимальный разрез() — это разрез с наименьшим значением суммы пропускных способностей дуг.

Если вершины неографа G = (X,U) разделены на два множества Хо и , где и является дополнением Хо относительно X, то множество ребер графа G, одни концевые вершины которых лежат в Хо, а другие — в Хо, определяют разрез этого неографа G.

Обозначают разрезы в графах R = (Х₀,).

 

Рис. 10.32

Разрез, состоящий из дуг орграфа определяется как объединение

Разрезом орграфа G2 (рис. 10.33) является множество дуг U₁ = (х₅, х₁), U2 = (x₁, x₄), U₄ = (х₃, х₇) и U5 = (х₂, х₇), удаление которых разделяет мно­жества вершин Хо = { х₁,х₂,х₃ } и ={ х₄,х₅,х₆,х₇ } (рис. 10.33).

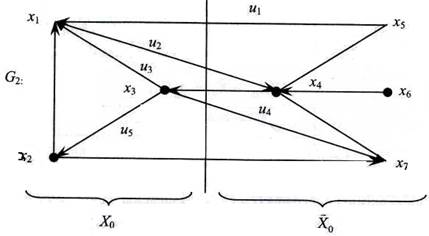Рис. 10.33

Этот разрез образован множествами:

Пример 10.2. Задача о максимальном потоке

Построить максимальный поток для ориентированной сети с источ­ником 5 и стоком t (рис. 10.34).

Пропускные способности дуг указаны на дугах сети:

Рис. 10.34

Решение

1. Составляем матрицу пропускных способностей дуг C = { c_ik } для графа G; нулевые значения пропускных способностей дуг в табл. 10.7 не записываем:

(10.7)

2. Выбираем произвольно один из путей от вершины S к вершине t графа G (рис. 10.34).

Пусть Р₁ = { s, x₁, x₄, t } —первоначальный путь: Определяем пропускную способность выбранного пути

Q₁ =min{10,5.13} = 5.

В табл. 10.7 отмечаем чертой сверху значения пропускных способно­стей дуг, соответствующих указанному пути Р₁. Вычитаем значение Q₁ = 5 из отмеченных элементов (10, 5, 13). Нули, получаемые в результате вы­числений, записываем в соответствующую строку или столбец.

(10.8)

3. Выбираем следующий путь из S в t, т.е. Р₂ = {s, x₄, t} и определяем его пропускную способность:

Q2 = min{4;8} = 4.

В табл. 10.8 отмечаем значения пропускных способностей чертой над числами 4 и 8. Вычитаем значение Q2 = 4 из указанных элементов. Полу­чаем новую табл. 10.9:

(10.9)

4. Выбираем новый путь из S в t, т.е.

Р₃ = { s, x_l, x₃, x₄, t }

и определяем его минимальную пропускную способность:

Q₃ =min{5,9,7,4} = 4.

Вычитаем значение Q₃ = 4 из элементов, отмеченных в табл. 10.9. По­лучаем табл. 10.10 в виде:

5. Выбираем путь Р₄ = {s,x3,£} и определяем его пропускную способ­ность:

Q₄ =min{14,2} = 2.

Вычитая Q₄ = 2 из значений пропускаемых способностей (14,2), полу­чаем табл. 10.11:

(10.11)

6. Укажем путь Р₅ = { s, x₂, t } и определим его пропускную способ­ность:

Q₅ = min{3;3} =3.

Вычитая Q₅ из элементов пропускных способностей дуг рассматри­ваемого пути получаем таб. 10.11 в виде 10.12:

(10.12)

В столбце t имеются только нули.

Следовательно, простроить новый путь невозможно.

Вычитая из элементов табл. 10.1) значения пропускных способностей дуг, указанных в табл. 10.12, получаем таблицу со значениями C_jk, опре­деляющими максимального возможный поток. Его величина равна

П = Q_l + Q₂ + Q₃ + Q₄ + Q₅;

П = 5 + 4 + 4 + 2 + 3 = 18.

Построим итоговую матрицу:

С₆ = С - С₅. (10.13)

(10.14)

На основании итоговой матрицы строим максимальный поток сети:

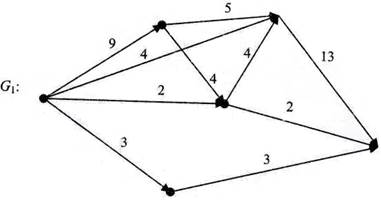Рис. 10.35

Построенный граф G удовлетворяют условию потока, т.е. соблюдает­ся равновесие вершин (величина входящего и выходящего потоков рав­ны). Величина минимального разреза дуг равна R = 18.

Рассмотрим другой способ решения задачи, используя алгоритм по­строения максимального потока в сети методом увеличения потока вдоль пути, который состоит в следующем:

1. Выбор начального потока. Обычно выбирают нулевое начальное значение потока.

2. Построение увеличивающегопути от источника 5 к стоку t

3. Увеличение потока вдоль построенного пути на максимально воз­можную величину, полагая увеличение потока по увеличивающей дуге и уменьшение его по уменьшающей дуге.

Увеличивающей дугой называется дуга, направление которой сов­падает с направлением потока и величина потока по этой дуге меньше ее пропускной способности, т.е.

Уменьшающей дугой называется дуга, направление которой проти­воположное направлению потока, а величина потока отлична от нуля:

Уменьшающие и увеличивающие дуги называют допустимыми.

Увеличивающим путем называется элементарный путь, все дуги ко­торого являются допустимыми.

Рассмотрим пример 10.2. Определить максимальный поток для сети (рис. 10.34).

Рис. 10.36

 

Решение.

1.Начальное значение потока полагаем равным нулю V_o — 0.

2.Построим увеличивающие пути от S к стоку t:

P_l = {s, x₁, x₄, t}, φ₁ = min (10; 5; 13) = 5.

Запишем значение φ₁ = 5 в скобках на соответствующих дугах рас­сматриваемого пути. Для пути (рис. 10.36)

Р₂ = {s, х₄, t}, φ ₂ = min (4; 13-5) = 4.

Отметим на дугах пути Р₂ величину φ ₂ = 4. Для пути

Р₃ = {s,x₁, x_3, x₄, t}, φ₃ = min (10-5; 9; 7; 13-9) = 4.

 

Запишем величину φ3 = 4 на дугах пути Р3. Аналогично запишем пути Р_i на дугах которых отметим соответствующие величины φ_i:

Р₄ = { s, х₃, t }, φ₄ = min (14; 2) = 2;

P₅ = { s, x₂, t }, φ₅ = min (6; 3) = 3.

Увеличивающих путей больше нет. Построим максимальный поток П_mах заданной сети (Рис.10.36)

Величина максимального потока равна сумме минимальных значе­ний φ_i, i = 1,2,3,4,5

П_mах = 5 + 4 + 4 + 2 + 3 = 18.

Значение минимального разреза R_min = 18.

Ответ: П_mах= R_min = 18.

ЗАДАЧА КОММИВОЯЖЕРА

Задача заключается в определении оптимального маршрута объезда n городов по критерию времени, стоимости или длине маршрута. Эта за­дача связана с определением гамельтонова цикла минимальной длины. Основным методом решения таких задач является метод ветвей и границ. Сущность метода заключается в том, что все множество допустимых ре­шений задачи делится на последовательно уменьшающиеся подмножест­ва с помощью процедуры ветвления. В результате находится последова­тельность объезда пунктов (маршрут), протяженность которого меньше любого другого возможного варианта, т.е. строится оптимальный коль­цевой маршрут.

Построить оптимальный кольцевой маршрут для неографа G(X,Y) (рис. 10.36) с вершинами х_i, Пропускные способности ребер указаны на графе.

1. Составим матрицу пропускных способностей ребер C(G) графа G(X,U) рис.10.37. Пропускную способность между однородными верши­нами условно принимаем равную бесконечности, т.е. (клет­ки главной диагонали матрицы С) (табл. 10.14).

Для определения нижней границы множества выполним приведение матрицы (табл. 10.14), т.е. в каждом столбце и строке матрица должна со­держать не менее одного нуля. С этой целью выберем в каждой строке минимальный элемент и запишем их в правой колонке табл. 10.14. Вычи­тая из элементов каждой строки соответствующие значения min a_ik, по­лучаем табл. 10.15.

k

Рис.10.37

 

 

(10.15)

 

Для завершения приведения матрицы табл. 10.15 вычитаем мини­мальные значения в каждом столбце min a_ik и получим приведенную матрицу (табл. 10.16). Сумма констант приведения по строкам и столбцам матрицы составит:

Н= 6 + 7 + 6+ 9+ 5 + 5 + 1+4 = 43.

Сумма констант приведения Н = 43 является границей всех циклов, т.е. любой вариант кольцевого маршрута не может быть меньше этой нижней границы.

С помощью ветвления рассматриваются циклы (последовательно­сти обхода вершин графа), которые могут привести к построению оп­тимального (минимального) кольцевого маршрута. На первом этапе построения древовидного графа множество всех циклов делится на два подмножества: первое из них включает все циклы (замкнутые маршру­ты) с перемещением от вершины х_i к вершине х_к, а второе множество содержит циклы без этого перемещения. На графе ветвления от исход­ной вершины Н = 43 отходят две дуги (ветви): к вершине (i,k), изобра­жающей первое из этих подмножеств и к вершине, указывающее второе (рис. 10.38).

Рис. 10.38

Рассмотрим, как выбирается пара вершин (i,k) и 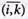. Пара вершин (x_i, х_k) на основании a(i,k), которые рассчитываются для всех клеток при­веденной матрицы (10.15), содержащих нули. Для определения a(i,k) в строке x_i выбирается минимальный элемент (c_{ik =} 0) и минимальный в столбце х_к. Эти минимальные элементы складываются, а их сумма равна значению a(i,k).

В рассматриваемом примере эти значения элементов в строках ука­жем справа, а в столбцах — внизу (табл. 10.16), сумму минимальных эле­ментов запишем в клетках, содержащих нули и отметим их кружком (табл. 10.16). Вычислим a(i,k) для каждой клетки с нулевым элементами:

(10.16)

 

Запишем значения α(i,k) в соответствующих клетках с нулями, от­мечая их кружками в табл. 10.16, выбираем наибольшее значение α(i,k) Таких значений в табл. 10.16 четыре. Выбираем одно из них, например, α(3,1) = 0 + 4 =4 (для строки х₃ и столбца x₁. Вычеркивая их, получаем табл. 10.17, в которой нуль, расположенный в строке х₁ и столбце х₃, заме­няем на . так как вершина х₃ не должна иметь цикла (3,1), т.е. c₁₃ =∞

 

(10.17)

Рис. 10.39

Определяем ребро ветвления, деля множества маршрутов на два: и (3,1), рис. 10.39. Нижняя граница вершины представляет сумму значений нижней границы предыдущей вершины, равной 43 и

т.е. Для определения нижней границы вершины вторым слагаемым берется сумма констант приведения матрицы 10.17. Для приведения этой матрицы из строки х1 следует вычесть минималь­ный элемент 4 и получим матрицу 10.18.

Сумма констант приведения равна h = 4. Нижняя граница вершины (3,1) составит H (3,1) = 43 + 4 = 47 (рис. 10.40).

(10.18)

Рис. 10.40

Для получения следующей пары вершин от вершины (3,1) опреде­лим а и выберем новую пару вершин, входящих в концевой маршрут. В табл. 10.18 укажем минимальные элементы в строках и столбцах, записанных справа и внизу этой таблицы соответственно. Вычислим сумму констант приведения a (i,k) и включим их в табл. 10.18:

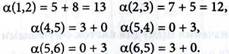
Принимаем вершины х₁ и х₂ с величиной приведения в качестве звена в кольцевом маршруте. В табл. 10.18 вычеркиваем столбец х₂ и получаем табл. 10.19:

 

(10.19)

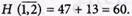Определяем вершины ветвления для ребер (1,2) и Нижняя гра­ница вершины определяется из условия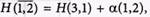

Для определения нижней границы вершины (1,2) вторым слагае­мым берем сумму констант приведения табл. 10.19, вычитая из строки х₂ а₂₅ = 7 и в столбце х₃ величину α₄₃ = 5, чтобы матрица имела нули в каж­дой строке и каждом столбце. Величина приведения h = 7 + 5. Н (1,2) = = 47 + 7 + 5 = 59.

Приведенная матрица табл. 10.20 имеет вид:

(10.20)

Определяем значения для клеток с нулевыми элементами:

Рис. 10.41

Исключаем из табл. 10.20 х₅ строку и столбец х₆. Получаем табл. 10.21:

(10.21)

Приведем табл. 10.21, вычитая из каждого элемента строки х₆ мини­мальный элемент а₆₄ = 3, Получаем табл. 10.22 в виде:

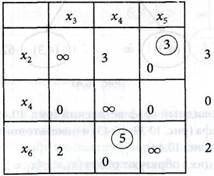
(10.22)

Строим подграф (рис. 10.42), исключаем в табл. 10.22 строку х₆ и стол­бец х₄, так как α (6,4) = 5. Получаем табл. 10.23, в которой α₄₄ = 0. Заменя­ем ∞ чтобы исключить цикл.

 

 

Рис. 10.42

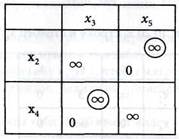
(10.23)

 

Рис. 10.43

Строим древовидный граф ветвлений (рис. 10.45), соединяя отдель­ные элементы графа (рис. 10.39-10.43) и гамельтонов цикл обхода вершин исходного графа (рис. 10.44).

Рис. 10.44

Гамельтонов цикл образуют ребра (x_3,x₁), (x_1,x₂), (х₂,х₅), (х_5,х₆), (х_6,х₄), (х₄,х₃).

Длина маршрута обхода вершин x_{3 →} x_{1 →} x_{2 →} x_5→ x_6→ x_{4 →} x₃ графа G(X,Y) (рис. 10. 37) составляет М = 6 + 11 + 14 + 5 + 12 + 14 = 62 и совпадает с нижней границей графа (рис. 10.45).

Рис. 10.45

Последовательность решения задачи коммивояжера методом ветвей играниц состоит в следующем:

1. На основании графа посещения городов составляется матрица расстояний от соответствующих вершин.

2. Проводится приведение матрицы, вычитая минимальные элемен­ты по строкам и столбцам.

3. Определяем нижнюю границу всего множества маршрутов, скла­дывая значения вычитаемых минимальных элементов.

 

4. В каждой клетке приведенной матрицы, в которых a_ik = 0, заменя­ем поочередно нули на ∞ и вычисляем суммы новых констант приведения H(x_i, x_k), которые записываем в клетке с нулем, отме­ченной кружком.

5. Выбираем ребро ветвления (i,k) по максимальной величине суммы констант приведения Н_тах. Затем исключаем его из множества пу­тем замены элемента матрицы а_1к =∞. В результате будет опреде­лено подмножество маршрутов {(i,k)}.

6. В полученной матрице расстояний по строкам получаем нули, вы­читая минимальное значение элементов в соответсвующих стро­ках и определяем нижнюю границу подмножества маршрутов H(i,k).

7. Включаем ребро (i,k) в маршрут, вычеркивая строку i и столбец к в приведенной матрице расстояний и заменяя симметричный эле­мент a_ik =∞ для исключения образования негамельтонова цикла.

8. Приводим сокращенную матрицу (получаем нули в строках вы­читанием минимального элемента) и определяем нижнюю грани­цу подмножества H(i,k).

9. Сравниваем нижние границы подмножеств H(i,k) и H (i,k) и под­множество с меньшим значением нижней границы подвергаем ветвлению.

10. Определяем гамельтонов цикл при получении окончательной мат­рицы размерности 2x2.

ЗАДАЧА О НАЗНАЧЕНИЯХ

«Лучший работник для выполнения данной работы» — вот подхо­дящее краткое описание задачи о назначениях. В этой задаче необходи­мо назначить работников на определенные работы. Каждый работник может выполнить любую работу, хотя и с различной степенью мастер­ства. Если на некоторую работу назначается работник именно той ква­лификации, которая необходима для ее выполнения, тогда стоимость выполнения работы будет ниже, чем при назначении на данную работу работника неподходящей квалификации. Цель задачи — найти опти­мальное (минимальной стоимости) распределение работников по всем заявленным работам.

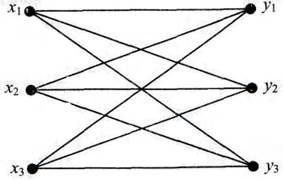Представление (связь) работников с соответствующими работами может быть представлена в виде:

а) графическое (рис. 10.46)

 

Рис. 10.46

б) матричное С = {c_ik},

c_ik — стоимость назначения i работника на к работу.

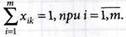
Постановка задачи состоит в следующем:

При ограничениях

n

∑ = x_ik = 1 при k = 1,n

^{k = 1}

Пример 10.3.

Требуется закрепить четырех работников А, В, С и D за четырьмя ра­ботами (I, II, III, IV) при условии минимизации суммарных затрат и выпол­нении одной работы одним работником, если после проведения хрономет­ража работ соответствующими работниками матрица задана в виде:

(10.24)

Приведем матрицу (10.24), т.е. упростим ее, вычитая из каждой стро­ки соответствующие минимальные элементы, получим (10.25):

(10.25)

Вычитаем минимальные значения в соответствующих столбцах мат­рицы (10.25), получим (10.26):

(10.26)

В соответствие с (10.26) допустимое решение не может быть найдено, так как нельзя выделить независимые нули. Увеличим количество нулей, выполняя следующие действия:

1. В матрице (10.26) приведем минимальное количество горизонталь­ных и вертикальных прямых по строкам и столбцам, чтобы вы­черкнуть все нулевые элементы.

2. Выбираем наименьший вычеркнутый элемент, равный 2. Таких элементов в (10.26) два. вычитаем его из остальных невычеркнутых элементов и прибавляем к каждому элементу, стоящему на пере­сечении проведенных прямых. В результате получаем матрицу в виде (10.27).

Выделяя независимые нули в (10.27) (это клетки а₁₁, а₃₂, а₂₃ а₄₄) полу­чаем решение задачи: работник А назначается на работу I, В на II, С на III, D на IV. Минимальные издержки определяем из условий:

(10.27)

C_min = 5+10+ 6 + 8 + 2 + 2 = 33,

т.е. сумма всех минимальных элементов, упрощающих матрицы, или

C_min = 5 + 8 + 12 + 8 = 33,

где слагаемые C_ik соответствуют независимым нулям матрицы. Эти эле­менты отмечены в (10.27).

При решении задач на максимум в каждом столбце выбирается мак­симальный элемент, из которого вычитаются все элементы этого столбца. Затем в каждой строке матрицы выбирается минимальный элемент, ко­торый вычитается из всех элементов этой строки. В результате этого в каждой сроке и в каждом столбце матрицы будет не менее одного нуля.

(10.28)

Распределить четырех работников из условия максимизации матрицы оценок (10.28). В каждом столбце матрицы (10.28) выбирается максималь­ный элемент и из него вычитаются все элементы этого столбца. Таким образом, получается матрица (10.29). Затем, вычитая минимальный эле­мент в каждой строке из остальных элементов, получаем табл. (10.30).

(10.29)

(10.30)

 

В матрице (10.30) выделим независимые нули, построив цепочку (под­черкнутые нули). Работник А закреплен за работой II, В — за работой IV, С — за работой III, D — за работой I.

Оценка С_mах = 7 + 13 + 14 + 10 = 44.

 

Поделиться:

Воспользуйтесь поиском по сайту: