Модели управления товарными запасами

Товарными запасами называются товары, которые находятся в среде обращения с момента их производства до момента реализации. Наличие товарных запасов является необходимым условием товарного обраще­ния. Управление товарными запасами включает задачи анализа, прогно­за, планирования и нормирования. Эти задачи решаются с помощью методов и моделей теории управления запасами.

Для оценки состояния и анализа тенденций развития запасов приме­няют относительные показания: уровень запасов в днях товарооборота и товарооборачиваемость. Товарный запас в днях товарооборота на опре­деленную дату показывает, на сколько дней торговли рассчитаны имею­щиеся в наличии товары. Товарооборачиваемость показывает, за сколько дней реализуется средний товарный запас.

Факторы, влияющие на товарные запасы, могут быть управляемыми и неуправляемыми. Например, к последним относится: удаленность по­ставщиков от торговых предприятий, условия транспортировки, нали­чие складских и подсобных помещений, магазинов и т.д.

Постановка задачи. При решении задач управления товарными за­пасами необходимо ответить на два вопроса.

1. Какое количество хранимого запаса следует заказать?

2. Когда заказывать товары?

Простейшей моделью оптимального размера партии поставки явля­ется модель Уилсона (рис.13.1.), основанная на следующих принципах:

1. Уровень запаса снижается равномерно в соответствии с равномер­но поступающими требованиями. Когда все запасы исчерпаны, подается заказ на поставку новой партии — S.

2. Выполнение заказа выполняется мгновенно, т.е. время доставки равно 0.

3. Накладные расходы, связанные с размещением заказа и поставкой партии, не зависит от объема партии и равны постоянной величи­не-К

Рис. 13.1

4. Издержки содержания единицы продукции в единицу времени равны h.

В задачах управления, когда в качестве критерия оптимальности вы­ступают суммарные издержки по управлению товарными запасами С. целевую функцию можно представить в общем виде [3]:

где С_х — затраты на хранение товаров за период I;

h — затраты на хране­ние одной единицы товара в течение года;

Z — величина среднего запаса, Z = S/2;

S — размер одной партии поставки товара;

Т — величина анали­зируемого периода (лет);

С₃ — затраты на транспортировку;

К — затраты на вывоз одной партии товара;

N — число поставок за анализируемый пе­риод Т;

Q — общий объем поставок товара за анализируемый период Т;

t_n — интервал поставок.

Целевую функцию можно представить в виде:

С = (h ∙(S/2) ∙T +К∙Q/S) → min

Неуправляемыми параметрами в целевой функции являются Q, Т, h, К. Это исходные данные для решения задачи. Остальные параметры — управляемые. Их оптимальные значения С^o_х, С^o₃, Z^o, п^o, t^o обеспечивают минимум издержек обращения. Для нахождения оптимальных величин этих параметров определяется экстремум целевой функции С = t(S) пу­темдифференцирования по S и приравнивания первой производной нулю:

Модели расчета оптимальных параметров системы управления одно-номенклатурными товарными запасами имеют вид:

1) Размер одной поставки товаров

2) Средний запас текущего хранения

 

3) Число поставок за период Т

4) Интервал между поставками

5) Величина минимальных издержек

 

Модели управления многономенклатурными запасами являются бо­лее сложными. В связи с этим при решении задач вводится предположе­ние, основанное на том, что отношения между затратами по поставке одной партии и затратами по хранению единицы товара по всем товар­ным позициям полагаются одинаковыми.

I. Оптимальные параметры товароснабжения определяют по сле­дующим моделям для каждой товарной позиции.

Определение размера партии:

 

Где — коэффициент пропорциональности между результативными и факторными признаками. Средний текущий запас:

Число поставок в днях:

Интервал поставок, в днях

Средневзвешенный товарный запас в днях:

Товарооборачиваемость определяется через показатели: время обращения

где q — среднедневной товарооборот, скорость оборота

Сравнение сложившихся показателей управления товарными запа­сами показывает, что количество поставок равное:

Потребность в товарных запасах снизится на величину, определяе­мую разностью по средневзвешенной:

Значение этой разности показывает величину экономии.

II. Определение основных показателей управления товарными запа­сами с учетом дефицита.

Плотность убытков из-за дефицита находят по зависимости:

где - — величина потерь на единицу товара в единицу времени,

h — за траты на хранение единиц товара в течение года.

Объем партии товара

Средний запас товара

Число поставок

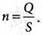
Интервал поставок в днях:

Время начисления дефицита товара

Средний объем дефицита спроса

Суммарные издержки управления составляют

Для выбора оптимальной системы товароснабжения необходимо сравнить потери в прибылях за счет нереализованной продукции.

Пример 13.1

На базу Роскульторга в течение года были доставлены радиотовары в следующем ассортименте, годовых объемах поставок Q₁ тыс. руб. и чис­ле поставок n₁ предоставленные в таблице

Таблица 13.1

 

Радиотовары	Q1 тыс. руб.	nо
Радиоприемники
Телевизоры
Магнитофоны
Электрофоны
Видеомагнитофоны
Радиодетали
Динамика

На основе приведенных данных о количестве поставок п₁ и объемах х годовые поставки Q₁ тыс. руб. по подгруппам определить сложившиеся показатели управления запасами S_i, Z_i, n_i, t_i, t, а затем оптимальные S_i⁰, Z_i⁰, n_i⁰_;, t_i⁰, t_i^-0. По группам и группе радиотоваров в целом.

Подсчитать экономию от снижения товарного запаса по товарной группе в целом.

Решение

1. Определяем сложившиеся показатели управления запасами S_i, Z _i, n_i, t_i, t. Результаты вычислений сведем в таблицу:

Таблица 13.2

 

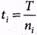
800 2300 160 140 1200 370 230	60 80 20 20 90 60 30	13,33 28,75 8 7 13,33 6,17 7,67	6,665 14,375 4 3,5 6,665 3,085 3,835	6,08 4,56 18,25 18,25 4,06 6,08 12,7	4864 10488 2920 2555 4872 2249,6 2799,1	28,28 47,96 12,65 11,83 34,64 19,24 15,17
		84,25	42,125	69,45	30747,7	169,77

2. Вычисляем коэффициент пропорциональности Н:

3. Определяем оптимальные параметры товароснабжения для каж­дой товарной группы. Результаты вычислений сведем в таблицу 13.3:

Таблица 13.3

 

13,29 22,54 5,95 5,56 16,28 9,04 7,13	60,17 102,04 26,91 25,17 73,70 40,94 32,28	6,645 11,27 2,975 2,78 8,14 4,52 3,565	6,07 3,58 13,56 14,50 4,95 8,92 11,31	4856 8234 2169,6 2030 5940 3300,4 2601,3
	361,21	39,9	62,9	29131,3

4. Определяем средневзвешенные значения по товарной группе в целом:

5. Находим экономию от снижения товарного запаса в целом:

 

Пример 13.2

Потребность микрорайона, обслуживаемого торговым предприяти­ем, в некотором товаре определена на плановый период Т = 2 года в объ­еме Q = 7-10⁵ кг. Стоимость организации заказа и поставки одной партии в магазин равна К - 50 тыс. руб. Издержки хранения единицы товара со­ставляют h = 0,28 тыс. руб./кг день. Необходимо определить оптимальные показатели управления товарными запасами: S°, t°, n°, t°, С°.

При заданных условиях рассчитать показатели управления товарны­ми запасами при наличии дефицита. Издержки дефицита составляемой С_g = 0,49 тыс. руб/кг день.

Решение

1. Размер одной поставки товаров составляет:

2. Средний запас текущего хранения:

3. Находим число поставок:

4. Вычисляем интервал между поставками:

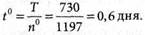
5. Определяем издержки управления товарными запасами:

Определяем основные показатели управления товарными запасами при наличии дефицита.

1. Вычисляем плотность убытков:

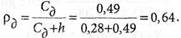
2. Определяем объем партии поставок:

3. Находим средний запас хранения товара с учетом дефицита:

4. Определяем число поставок:

5. Находим интервал между поставками:

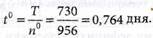
6. Вычисляем время наличия дефицита:

7. Определим суммарные издержки управления товарными запасами:

Стохастический вариант модели экономичного размера заказа

В новой модели допускается неудовлетворенный спрос, как это пока­зано на рисунке. В рассматриваемой модели заказ размером у размеща­ется тогда, когда объем запаса достигает уровня R. Как и в детерминиро­ванном случае, уровень R, при котором снова размещается заказ, явля­ется функцией периода времени между размещением заказа и его выпол­нением. Оптимальные значения y и R определяются путем минимизации ожидаемых затрат системы управления запасами, отнесенных к единице времени, которые включают как расходы на размещение заказа и его хра­нение, так и потери, связанные с неудовлетворенным спросом.

В рассматриваемой модели приняты три допущения.

1. Неудовлетворенный в течение срока выполнения заказа спрос на­капливается.

2. Разрешается не более одного невыполненного заказа.

3. Распределение спроса в течение срока выполнения заказа являет­ся стационарным (неизменным) во времени.

Для определения функции, отражающей суммарные затраты, отне­сенные к единице времени, введем следующие обозначения:

f(x) — плотность распределения спроса х в течение срока выполнения заказа;

Q — ожидаемое значение спроса в единицу времени;

h — удельные затраты на хранение (на единицу продукции за едини­цу времени);

р — удельные потери от неудовлетворенного спроса (на единицу про­дукции за единицу времени); К — стоимость размещения заказа.

Основываясь на этих определениях, вычислим компоненты функций затрат.

1. Стоимость размещения заказов. Приближенное число заказов в единицу времени равно Q/y, так что стоимость размещения заказов в единицу времени равна KQ/y.

2. Ожидаемые затраты на хранение. Средний уровень запаса равен

Следовательно, ожидаемые затраты на хранение за единицу времени равны hI.

Приведенная формула получена в результате усреднения ожидаемых в начале и конце временного цикла, т.е. величин y + M{R-x} и M{R-x} соответственно. При этом игнорируется случай, когда величина R - М{х} может быть отрицательной, что является одним из упрощающих допу­щений рассматриваемой модели.

3. Ожидаемые потери, связанные с неудовлетворенным спросом. Де­фицит возникает при х > R. Следовательно, ожидаемый дефицит за еди­ницу времени равен

Так как в модели предполагается, что р пропорционально лишь объ­ему дефицита, ожидаемые потери, связанные с неудовлетворенным спро­сом, за один цикл равны pS. Поскольку единица времени содержит Q/y циклов, то ожидаемые потери, обусловленные дефицитом, составляют pQS/y за единицу времени.

Результирующая функция общих потерь за единицу времени TCU имеет следующий вид

оптимальное значение у* и R* определяется из представленных ниже уравнений.

Следовательно, имеем

Так как из последних двух уравнений нельзя определить у* и R* в яв­ном виде, для их нахождения используется численный алгоритм, пред­ложенный Хедли и Уйтин. Доказано, что алгоритм сходится за конечное число итераций при условии, что допустимое решение существует.

При R = 0последние два уравнения соответственно дают следующее

Числительная процедура определяет, что наименьшим значением у* является которое достигается при S = 0.

 

Пример 13.3

Хлебокомбинат г. Батайска использует в производстве муку в коли­честве 45х10⁴ кг в месяц. Размещение заказа на новую поставку муки обходится в 1000 руб., стоимость хранения одного кг муки на протяжении одного месяца равна 10 руб., а удельные потери от ее дефицита — 26 руб. за 1 кг. Статистические данные свидетельствуют о том, что спрос в пери­од поставки является случайной величиной, равномерно распределенной от 0 до 1000 кг. Определить оптимальную политику управления запасами для комбината.

Используя принятые в модели обозначения, имеем следующее:

Q = 45*10 кг в месяц,

К = 1000 руб. = 10 руб. за размещение заказа,

h = 15 руб. за один кг в месяц,

р = 26 руб. за один кг,

f(x) = 1/1000,0<х<100,

М(х) = 1000 кг = 10³ кг.

Сначала необходимо проверить, существует ли допустимое решение задачи.

Используя уравнения для у¯ и у^~, получаем следующее:

Так как у^~> у¯, значит существует единственное решение для у* и R*. Выражение для S записывается в следующем виде:

Используя вуравнениях выражения для S, получаем следующее:

Из последнего уравнения имеем:

Теперь используем последние уравнения для нахождения решения.

Итерация 1.

Итерация 2.

Следовательно,

Итерация 3

Так как значения R₂ и R₃ примерно одинаковы, приближенное опти­мальное решение определяется значениями R*≈ 984 кг, у* ≈ 7758 кг.

Следовательно, оптимальное управление товарными запасами состо­ит в размещении заказа примерно на 7758 кг, как только запас уменьша­ется до 984 кг.

Стохастический вариант решения задачи наиболее оптимальный, так как он учитывает спрос покупателей, дефицит товара, что необходимо для нормальной работы.

Задачи 13.1-13.4

№ 13.1

В течение года на оптовую базу были поставлены спортивные това­ры в ниже перечисленном ассортименте, в годовых объемах поставок Q_i; млн. руб. и числе поставок п_i.

 

Спортивные товары	Qi	пi.
Обувь
Туристические товары
Трикотаж
Швейные товары
Спортивный инвентарь
Прочие спорт товары

Определить показатели системы управления запасами при сложив­шихся S_i, Z_i, n_i, t_i, t, а затем оптимальные S_i⁰, Z_i⁰, n_i⁰_;, t_i⁰, t_i^-0. Опре­делить экономию от снижения товарного запаса по товарной группе в целом.

№13.2

На оптовую базу Роскульторга в течение года были поставлены му­зыкальные товары в следующем ассортименте годовых объемов поставок Q_i, млн. руб. и числе поставок п_i:

 

Музыкальные товары	Qi,	пi
Смычковые
Щипковые
Баяны
Гармони
Духовые
Самоучители

Определить сложившееся показатели управления запасами S_i, Z_i, n_i, t_i, t, а затем оптимальные S_i⁰, Z_i⁰, n_i⁰_;, t_i⁰, t_i^-0.. Вычислить экономию от сни­жения товарного запаса по товарной группе в целом.

№ 13.3

На оптовую базу Роскульторга в течение года были поставлены радио­товары в следующем ассортименте, годовых объемов поставок Q_i млн руб. и числе поставок п_i.

 

Радиотовары	Qi	пi
Радиоприемники
Телевизоры
Магнитофоны
Радиодетали
Динамики
Музыкальные центры

На основе приведенных данных определить сложившиеся показатели управления запасами при сложившихся условиях S_i, Z_i, n_i, t_i, t, а затем оптимальные S_i⁰, Z_i⁰, n_i⁰_;, t_i⁰, t_i^-0 по подгруппам и группе в целом.

Найти экономию от снижения товарного запаса по товарной группе в целом.

№ 13.4

В розничное торговое предприятие в течение года были поставлены часы в следующем ассортименте, годовых объемах поставок Q_i млн. руб., и числе поставок п_i

 

Часы	Qi	пi
Наручные
Карманные
Настенные
Будильники
Настольные

На основе приведенных данных определить сложившиеся показатели управления запасами S_i, Z_i, n_i, t_i, t, а затем оптимальные S_i⁰, Z_i⁰, n_i⁰_;, t_i⁰, t_i^-0 пo подгруппам и группе в целом. Найти экономию от снижения товарного запаса по товарной группе в целом.

Задачи № 13.5-13.10

Потребность микрорайона, обслуживаемого торговым предприяти­ем, в товаре определена на период Т в объеме Q_i, кг. Стоимость организа­ции заказа и поставки одной партии в магазин равна круб. Издержки хранения единицы товара составляют h руб. за 1 кг в день. Пологая, что спрос на эти товары стабильный, определить оптимальные показатели управления товарными запасами S_i⁰, Z_i⁰, n_i⁰_;, t_i⁰ С⁰. Определить показате­ли управления запасами этого же товара при наличии дефицита, если потери из-за несвоевременной реализации товара, т.е. издержки, состав­ляют С_д руб. за кг в день. Данные в табл. 13.4:

Таблица 13.4

 

Номера задач	Наименование товара	Спрос за период Т	Издержки	Плановый период
К	h	Сд
Q, кг	руб.	руб. /кг дн	руб./кг дн	Т, лет
	Мука	7*105		2,0	5,0	2,5
	Рис	9,5*105		2,5	5,5	2,0
	Сахар	12,5*105		3,5	6,0	1,5
	Крупа	14,0*105		4,0	6,5	2,5
	Масло	6*105		4,0	7,0	2,5
	Мясо	8*105		5,0	7.5	3.0

Контрольные вопросы

1. Назовите показатели и факторы, влияющие на товарные запасы.

2. Что определяет критерий оптимальности управления товарными за­пасами?

3. Какие основные параметры определяют товарные запасы?

 

4. Сформулируйте постановку задачи управления товарными запасами для одной группы товаров.

5. Укажите зависимость издержек обращения от размера партии по­ставки.

6. Назовите факторы, влияющие на модели анализа и прогноза товар­ных запасов.

7. Методы решения задач управления товарными запасами с учетом дефицита.

8. Стохастическая модель управления товарными запасами

Поделиться:

Воспользуйтесь поиском по сайту: