 |
Касательные напряжения при поперечном изгибе. Формула Журавского.
|
|
|
|
Потенциальная энергия упругой деформации при растяжении-сжатии
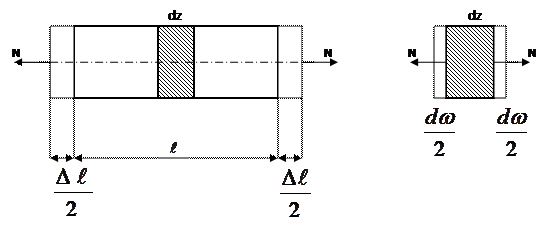
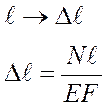
s = Eε – закон Гука
EF – жёсткость при растяжении-сжатии;
F – площадь;
E – модуль Юнга.
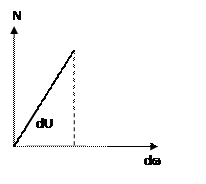
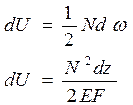dU – потенциальная энергия упругой деформации
10.
Статически неопределимыми называются системы, в которых внутренние силовые факторы не могут быть определены из основных уравнений равновесия (число неизвестных больше числа уравнений статики).
Степень статической неопределимости – разность между числом неизвестных (в опорах или заделках) и число уравнений равновесия.
Для раскрытия статической неопределимости составляют дополнительные уравнения перемещения (совместности деформации), их число равно степени статической неопределимости системы.
HB=0, HA=0;
MA=0, MB=0
RA=2P/3, RB=-P/3
1. Статическая сторона задачи:
Основное уравнение равновесия (уравнение статики)
SFi(z) = -RA + P + RB =0
2 неизвестных -1 уравнение равновесия = система 1 раз статически неопределима
2. Геометрическая сторона задачи:
Дополнительное уравнение равновесия (уравнение совместности деформации)
3. Физическая сторона задачи:
Dl1 + Dl2 =0
12.
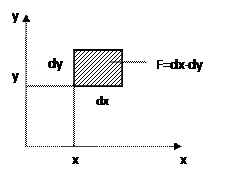
Статические моменты сечения
Статические моменты сечения – это интегралы вида:
[ L3 ]
Центром тяжести относительно осей х и у, называется точка С (хс, ус), которая вычисляется по формуле:
Если оси х и у проходят через точку С, то хс=0 и ус=0, и отсюда следует, что Sx =0, Sy =0.
Декартова система координат
|
Полярная система координат
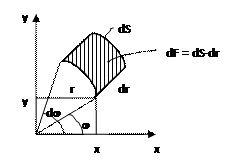
Определим статический момент полукруга
xc=0 (в силу симметрии относительно оси у)
yc=?
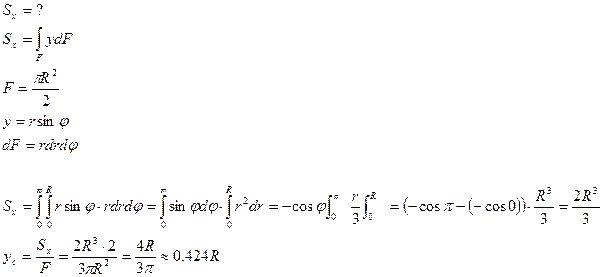
13. Моменты инерции простых сечений.
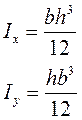
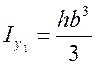
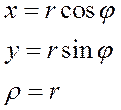
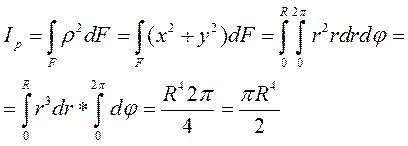
Центр тяжести совпадает с центром координат
|
|
|
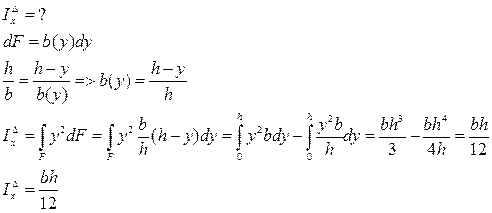
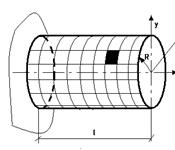
Кручение бруса с круглым поперечным сечением
Кручение – такой вид нагружения бруса, при котором в его поперечном сечении возникает только один внутренний силовой фактор, отличный от нуля, называемый крутящий момент.
Мкр или Мz
Пример конструкции, работающей на кручение – вал.
φ – угол кручения
Закон Гука для кручения.
τ=σ*γ
до деформации после деформации
Опыт показывает, что расстояние между скручиваемыми волокнами вала не изменяется, продольные линии сетки приобретают винтовые формы, винтовые углы сетки искажаются как в случае сдвига.
Следствия: выделяемый элементарный объем материала находится в условиях чистого сдвига, радиусы остаются прямыми и неизменной длины.
Нижележащие слои (глубжележащие (ближе к центру)) испытывают меньшую деформацию, а максимума деформация достигает по образующей поверхности цилиндра (R – max).
dS=ρ*dφ
γ~tgγ=dS/dz
 |
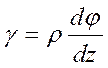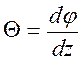
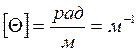- относительный угол закручивания
G – модуль сдвига 
, 
- жесткость при кручении
[G JP]= 
=H*M2
Gстали=0,8 МПа (Естали=2*105МПа)
G<E (всегда)
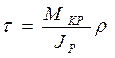
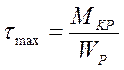
формула для определения касательных напряжений при кручении
16.
Дифференциальные зависимости при изгибе.
1).∑Fi(Y)=Qy+qy(z)dz-(Qy+dQy)=0
qy(z)dz - dQy=0
2). 
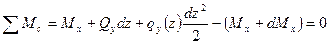
Qydz=dMx → 
Теорема Журавского: полная производная, взятая по длине от поперечной силы, равна интенсивности распределения нагрузки.
Полная производная от изгибающего момента, взятая по длине, равна поперечной силе.
Вторая производная от изгибающего момента равна интенсивности распределенной нагрузки.
17.
Линейное напряженное состояние возникает при центральном и/или внецентринном растяжении – сжатии, при чистом и косом изгибе.
- нормаль к наклонной площадке
-вектор полного
нормального напряжения;
- нормальное напряжение;
- касательное напряжение.
|
|
|
а) 
- 
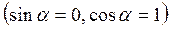
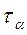- напряжение, действующее на главную площадку.
б). 
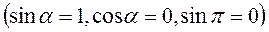
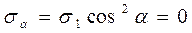
- главная площадка.
в).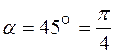 
18.
Касательные напряжения при поперечном изгибе. Формула Журавского.
Касательные напряжения ввиду своей парности всегда именуются двумя индексами: 1-й индекс соответствует той оси, которой они перпендикулярны,
| |
| |
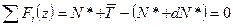
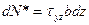
| (1) |
| |
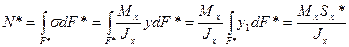
| (2) |
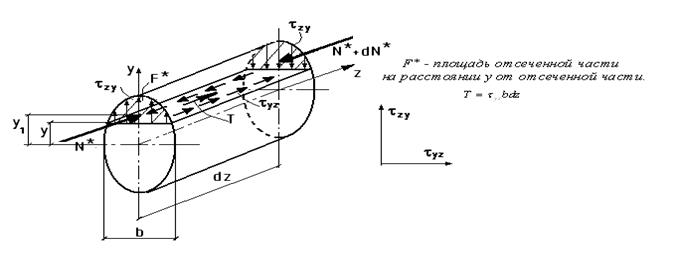2-индекс соответствует оси, которой они параллельны.
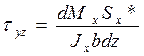
(1)=(2):
- формула Журавского
Qy – поперечная сила – const для любой точки поперечного сечения;
Jx – момент инерции сечения – постоянная величина для всего сечения относительно оси Х;
b – ширина сечения в рассматриваемой точке, b≠const;
Sx* - статический момент отсеченной части сечения площадью F*:
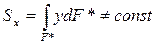
Максимального значения касательные напряжения достигают в центре тяжести сечения: статический момент максимален из-за максимального значения площади F*.
Минимального значения касательные напряжения достигают по верхней и нижней границе сечения.
Пример:
Опасное сечение – заделка.
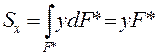(для прямоугольника)
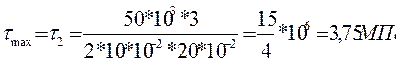
При проведении прочностных расчетов из-за малости касательных напряжений ими часто пренебрегают.
Формула Журавского справедлива для достаточно узких и высоких профилей балки: b<<h, т.к. предполагается, что касательные напряжения равномерно распределены по ширине сечения, что подтверждается экспериментально.
Для балок иных профилей формула Журавского носит приближенный характер
|
|
|
