 |
Уравнения математической физики
|
|
|
|
Решение типового (чётного) варианта
Задача № 1. Определить тип уравнения и привести его к каноническому виду:
 . (1.1)
. (1.1)
Решение. Уравнению (1.1) соответствует квадратичная форма
 ,
,
где  ,
,  ,
,  .
.
Так как  , то заданное уравнение имеет гиперболический тип и, значит, имеет два семейства характеристик. Их дифференциальные уравнения
, то заданное уравнение имеет гиперболический тип и, значит, имеет два семейства характеристик. Их дифференциальные уравнения



После интегрирования получим уравнения двух семейств характеристик для дифференциального уравнения (1.1):
 ;
;  . (1.2)
. (1.2)
Согласно уравнениям характеристик (1.2) вводим замену  ,
, 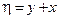 . Применяя формулы дифференцирования сложной функции двух переменных, выразим частные производные по старым переменным через частные производные по новым переменным:
. Применяя формулы дифференцирования сложной функции двух переменных, выразим частные производные по старым переменным через частные производные по новым переменным:
 ;
;  ;
;

 ;
;


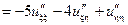 ;
;

 .
.
Подставив эти производные в уравнение (1.1), получим



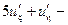
 ,
,
т.е.  . Сокращая на
. Сокращая на  , приходим к уравнению канонического вида
, приходим к уравнению канонического вида
 . (1.3)
. (1.3)
Задача № 2. Найти решение  уравнения
уравнения
 , (2.1)
, (2.1)
удовлетворяющее начальным условиям
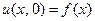 ,
,  ,
, 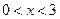 (2.2)
(2.2)
и граничным условиям
 ,
,  ,
,  . (2.3)
. (2.3)
Вид функций  и
и  изображён на рисунке 2.1 (
изображён на рисунке 2.1 ( ;
;  ;
;  ;
;  ).
).
Решение. Найдём аналитические выражения для функций  и
и  . Уравнение прямой
. Уравнение прямой  (рис. 2.1) запишем как уравнение прямой, проходящей через точку
(рис. 2.1) запишем как уравнение прямой, проходящей через точку  и имеющей угловой коэффициент
и имеющей угловой коэффициент  , то есть
, то есть  :
: 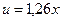 . Аналогично запишется уравнение прямой
. Аналогично запишется уравнение прямой  как уравнение прямой, проходящей через точку
как уравнение прямой, проходящей через точку  и имеющей угловой коэффициент
и имеющей угловой коэффициент  , то есть
, то есть  :
:  . Следовательно, начальные условия (2.2) имеют вид
. Следовательно, начальные условия (2.2) имеют вид

|
| Рис. 2.1 |

 (2.4)
(2.4)
Задачу будем решать методом Фурье (методом разделения переменных). Частные, не равные тождественно нулю, решения уравнения (2.1), удовлетворяющие граничным условиям (2.3) будем искать в виде произведения двух функций, одна из которых зависит только от  , а другая – только от
, а другая – только от  , то есть
, то есть
 , (2.5)
, (2.5)
где  и
и  – функции, подлежащие определению. Функцию
– функции, подлежащие определению. Функцию 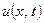 из (2.5) подставим в уравнение (2.1). Получим
из (2.5) подставим в уравнение (2.1). Получим
|
|
|
 .
.
Отсюда, разделяя переменные, находим
 . (2.6)
. (2.6)
Равенство (2.6), левая часть которого не зависит от  , а правая – от
, а правая – от  , возможно лишь в том случае, если обе его части не зависят ни от
, возможно лишь в том случае, если обе его части не зависят ни от  , ни от
, ни от  , то есть представляют собой одну и ту же постоянную, которую обозначим через
, то есть представляют собой одну и ту же постоянную, которую обозначим через 
 . Тогда
. Тогда
 .
.
Следовательно, получаем два уравнения относительно функций  и
и  :
:
 (2.7)
(2.7)
и
 . (2.8)
. (2.8)
Удовлетворим  граничным условиям (2.3)
граничным условиям (2.3)
 ,
,  (2.9)
(2.9)
и найдём такие значения 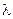 , при которых существуют отличные от нуля решения уравнения (2.8). Для нахождения общего решения уравнения (2.8) составим характеристическое уравнение
, при которых существуют отличные от нуля решения уравнения (2.8). Для нахождения общего решения уравнения (2.8) составим характеристическое уравнение
 .
.
Корнями этого уравнения являются  , и, следовательно, общее решение уравнения (2.8) имеет вид
, и, следовательно, общее решение уравнения (2.8) имеет вид
 .
.
Подставим это решение в соотношения (2.9). Тогда

Решая систему, получим  ,
,  ;
;  ,
,  , что возможно только в случае
, что возможно только в случае  . Отсюда собственные значения задачи Штурма – Лиувилля, то есть такие значения
. Отсюда собственные значения задачи Штурма – Лиувилля, то есть такие значения 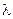 , при которых задача (2.8), (2.9) имеет нетривиальные решения, равны
, при которых задача (2.8), (2.9) имеет нетривиальные решения, равны  ,
,  Тогда решения этой задачи (собственные функции) имеют вид
Тогда решения этой задачи (собственные функции) имеют вид
 ,
, 
Найдём теперь общее решение уравнения (2.7) при  . Для этого составим характеристическое уравнение
. Для этого составим характеристическое уравнение
 .
.
Корнями этого уравнения будут  , и, следовательно, общее решение уравнения (2.7) имеет вид
, и, следовательно, общее решение уравнения (2.7) имеет вид
 .
.
Полагая в этом выражении  ,
,  , получаем
, получаем
 .
.
Тогда

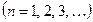 .
.
Каждому значению  отвечают свои постоянные
отвечают свои постоянные  и
и  , поэтому пишем
, поэтому пишем 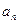 и
и  , а постоянную
, а постоянную  включаем в
включаем в 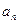 и
и  .
.
Так как уравнение (2.1) линейное и однородное, то функция
 (2.10)
(2.10)
является решением уравнения (2.1), удовлетворяющим граничным условиям (2.3).
Определим теперь  и
и  так, чтобы решение (2.10) удовлетворяло и начальным условиям (2.4), то есть
так, чтобы решение (2.10) удовлетворяло и начальным условиям (2.4), то есть
 ,
, 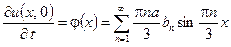 . (2.11)
. (2.11)
Функции 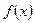 и
и  разлагаются в ряд Фурье в промежутке
разлагаются в ряд Фурье в промежутке  по синусам, и тогда
по синусам, и тогда
 . (2.12)
. (2.12)
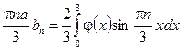 . (2.13)
. (2.13)
Подставляя выражения (2.4) для функций  и
и  соответственно в (2.12) и (2.13), находим
соответственно в (2.12) и (2.13), находим
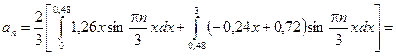






 ;
;


 .
.
Найденные значения 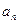 и
и  подставим в (2.10) и получим искомое решение в виде
подставим в (2.10) и получим искомое решение в виде
|
|
|
 .
.
Задача № 3. Методом Фурье найти решение  уравнения
уравнения
 , (3.1)
, (3.1)
удовлетворяющее начальному условию
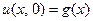 ,
,  (3.2)
(3.2)
и граничным условиям
 ,
,  ,
,  . (3.3)
. (3.3)
Вид функции  изображён на рисунке 3.1 (
изображён на рисунке 3.1 ( ;
;  ;
;  ;
; 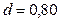 ).
).
Решение. Найдём аналитические выражения для функции  . Функция
. Функция  при
при  . В интервале
. В интервале  запишем
запишем  в виде уравнения прямой, проходящей через точку
в виде уравнения прямой, проходящей через точку  и имеющей угловой коэффициент
и имеющей угловой коэффициент  . Тогда в этом интервале
. Тогда в этом интервале
 .
.
С учётом полученных выражений начальное условие (3.2) запишем в виде
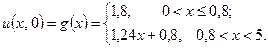 (3.4)
(3.4)
 Рис. 3.1
Рис. 3.1
|
Так как граничные условия не нулевые, то метод Фурье для решения задачи (3.1) – (3.3) не применим. Поэтому введём новую функцию
 , (3.5)
, (3.5)
где  и
и 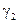 – постоянные, которые надо определить так, чтобы
– постоянные, которые надо определить так, чтобы
 ,
,  ,
,  . (3.6)
. (3.6)
Итак,
 , (3.7)
, (3.7)
 . (3.8)
. (3.8)
Из системы уравнений

имеем  ,
,  . Тогда
. Тогда
 . (3.9)
. (3.9)
Подставляя функцию  из (3.9) в уравнение (3.1), получим уравнение для функции
из (3.9) в уравнение (3.1), получим уравнение для функции  :
:
 , (3.10)
, (3.10)
а начальные и граничные условия примут вид:
 (3.11)
(3.11)
 ,
,  ,
,  . (3.12)
. (3.12)
Теперь для решения краевой задачи (3.10) – (3.12) можно применить метод Фурье. Пусть
 . (3.13)
. (3.13)
Подставляя (3.13) в (3.10) и разделяя переменные, получим
 ,
,  . (3.14)
. (3.14)
Из (3.14) получаем уравнения для определения  и
и  :
:
 , (3.15)
, (3.15)
 . (3.16)
. (3.16)
Общие решения этих уравнений имеют вид
 , (3.17)
, (3.17)
 . (3.18)
. (3.18)
Для нахождения постоянных 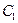 и
и  воспользуемся граничными условиями (3.12). Функция
воспользуемся граничными условиями (3.12). Функция  , как следует из (3.12), удовлетворяет граничным условиям
, как следует из (3.12), удовлетворяет граничным условиям
 ,
,  . (3.19)
. (3.19)
Подставим (3.18) и  в граничные условия (3.19) Тогда
в граничные условия (3.19) Тогда
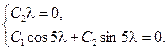
Решая эту систему уравнений и учитывая, что ищется ненулевое решение задачи Штурма – Лиувилля (3.16), (3.19), получим
 ,
,  ,
,  ,
,  ,
,  ,
, 
Найденным собственным значениям  задачи соответствуют собственные функции
задачи соответствуют собственные функции
 ,
, 
Общее решение (3.17) уравнения (3.15) при  примет вид
примет вид
 .
.
Тогда в соответствии с представлением решения  в виде (3.13) получим частные решения уравнения (3.10) в виде
в виде (3.13) получим частные решения уравнения (3.10) в виде
 ,
, 
Запишем теперь решение краевой задачи (3.10) – (3.12):
 , (3.20)
, (3.20)
где  – пока неизвестные постоянные, определяемые из начального условия (3.11). Полагая
– пока неизвестные постоянные, определяемые из начального условия (3.11). Полагая  в (3.20) и учитывая (3.11), получим
в (3.20) и учитывая (3.11), получим
 .
.
Отсюда найдём коэффициенты 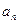 этого тригонометрического ряда Фурье:
этого тригонометрического ряда Фурье:




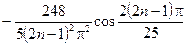 .
.
Подставляя найденные значения 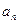 в (3.20) и учитывая (3.9), получим искомое решение в виде
в (3.20) и учитывая (3.9), получим искомое решение в виде
 .
.
Задача № 4. Найти стационарное распределение температуры в прямоугольной пластинке  , если известны значения температуры на границе пластинки:
, если известны значения температуры на границе пластинки:
|
|
|
 ,
,  ,
,  ;
;
(4.1)
 ,
,  ,
,  .
.
Решение. Стационарное распределение температуры в прямоугольной пластинке описывается уравнением Лапласа
 . (4.2)
. (4.2)
Так как на границе пластинки заданы условия (4.1), то поставленная задача есть задача Дирихле для квадрата. Граничные условия не являются однородными (нулевыми) на параллельных сторонах квадрата. Поэтому для нахождения решения 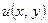 краевой задачи (4.2), (4.1) представим его в виде суммы
краевой задачи (4.2), (4.1) представим его в виде суммы
 , (4.3)
, (4.3)
где обе функции  и
и  удовлетворяют уравнению Лапласа, но
удовлетворяют уравнению Лапласа, но  подчиняется граничным условиям
подчиняется граничным условиям
 ,
, 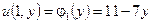 ,
,  ;
;
(4.1)
 ,
, 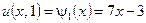 ,
,  .
.
а 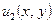 – граничным условиям
– граничным условиям
 ,
,  ,
,  ,
,
(4.5)
 ,
,  ,
,  .
.
Функции  и
и 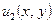 будем искать методом Фурье. Функцию
будем искать методом Фурье. Функцию  представим в виде
представим в виде
 , (4.6)
, (4.6)
где  и
и  – некоторые неизвестные функции.
– некоторые неизвестные функции.
Для отыскания функций  и
и  функцию
функцию  подставим в уравнение (4.2). Тогда
подставим в уравнение (4.2). Тогда
 .
.
Следовательно,
 , (4.7)
, (4.7)
где  – постоянная величина. Таким образом,
– постоянная величина. Таким образом,  и
и  есть решения обыкновенных дифференциальных уравнений
есть решения обыкновенных дифференциальных уравнений
 , (4.8)
, (4.8)
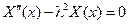 , (4.9)
, (4.9)
причём согласно нулевым граничным условиям из (4.4)
 ,
,  . (4.10)
. (4.10)
Найдём решение задачи Штурма – Лиувилля (4.8), (4.10). Характеристическое уравнение для дифференциального уравнения (4.8) имеет вид


 .
.
Запишем теперь общее решение уравнения (4.8):
 . (4.11)
. (4.11)
Удовлетворим это решение условиям (4.10):

Отсюда
 ,
,  ,
,  ,
, 
Таким образом, собственные значения и собственные функции задачи Штурма – Лиувилля имеют вид
 ,
,  ,
,  .
.
При  уравнение (4.9) примет вид
уравнение (4.9) примет вид
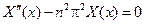 .
.
Отсюда находим общее решение этого уравнения:
 ,
,
где  и
и  – произвольные постоянные.
– произвольные постоянные.
Функции 
 удовлетворяют уравнению (4.2) и нулевым граничным условиям на сторонах квадрата
удовлетворяют уравнению (4.2) и нулевым граничным условиям на сторонах квадрата  и
и  . Этим же условиям будет удовлетворять сумма функционального ряда
. Этим же условиям будет удовлетворять сумма функционального ряда
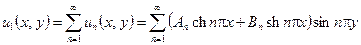 , (4.12)
, (4.12)
при условии возможности его почленного дифференцирования.
Определим  и
и  так, чтобы функция
так, чтобы функция  удовлетворяла и двум другим условиям из (4.4). Подставим решение (4.12) в граничные условия (4.4). Получим соотношения
удовлетворяла и двум другим условиям из (4.4). Подставим решение (4.12) в граничные условия (4.4). Получим соотношения
 (4.13)
(4.13)
Ряды в правых частях этих соотношений представляют собой разложения функций  и
и 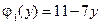 в тригонометрический ряд Фурье по синусам на интервале
в тригонометрический ряд Фурье по синусам на интервале  . Из первого уравнения системы находим
. Из первого уравнения системы находим

 .
.
Из второго уравнения системы получаем
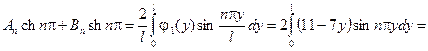

 .
.
Отсюда
|
|
|
 ,
,
 .
.
Подставим найденные значения коэффициентов разложения  и
и  в (4.12). Тогда
в (4.12). Тогда

 . (4.14)
. (4.14)
Найдём решение 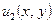 , удовлетворяющее граничным условиям (4.5), тем же способом, что и функцию
, удовлетворяющее граничным условиям (4.5), тем же способом, что и функцию  , то есть представим частное решение краевой задачи для
, то есть представим частное решение краевой задачи для 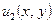 в виде
в виде
 ;
;
найдём собственные значения  и собственные функции
и собственные функции  задачи Штурма – Лиувилля
задачи Штурма – Лиувилля
 , (4.15)
, (4.15)
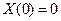 ,
, 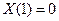 ; (4.16)
; (4.16)
запишем общее решение уравнения
 , (4.17)
, (4.17)
определяющего функцию  при
при  ; представим затем решение
; представим затем решение 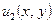 в виде
в виде
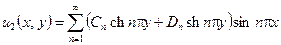 . (4.18)
. (4.18)
Коэффициенты  и
и  определяются в результате подстановки (4.18) в ненулевые граничные условия (4.5):
определяются в результате подстановки (4.18) в ненулевые граничные условия (4.5):
 (4.19)
(4.19)
Отсюда

 .
.

 .
.
Следовательно,
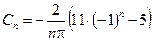 ;
;  .
.
Подставим найденные значения  и
и  в выражение (4.18), получим
в выражение (4.18), получим

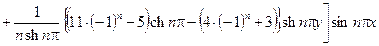 .
.
Окончательное решение исходной краевой задачи находим в виде




 .
.
Работу выполнил: дата, подпись.
|
|
|


