 |
Уравнения математической физики
|
|
|
|
Решение типового (нечётного) варианта
Задача № 2. Найти решение  уравнения
уравнения
 , (2.1)
, (2.1)
удовлетворяющее начальным условиям
 ,
,  ,
,  (2.2)
(2.2)
и граничным условиям
 ,
,  ,
,  . (2.3)
. (2.3)
Вид функций  и
и 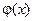 изображён на рисунке 2.1 (
изображён на рисунке 2.1 ( ;
;  ;
;  ;
;  ).
).
Решение. Найдём аналитические выражения для функций  и
и 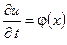 . Уравнение прямой
. Уравнение прямой  (рис. 2.1) запишем как уравнение прямой, проходящей через точку
(рис. 2.1) запишем как уравнение прямой, проходящей через точку  и имеющей угловой коэффициент
и имеющей угловой коэффициент  , то есть
, то есть  :
:  . Аналогично запишется уравнение прямой
. Аналогично запишется уравнение прямой  как уравнение прямой, проходящей через точку
как уравнение прямой, проходящей через точку  и имеющей угловой коэффициент
и имеющей угловой коэффициент  , то есть
, то есть  :
:  . Следовательно, начальные условия (2.2) имеют вид
. Следовательно, начальные условия (2.2) имеют вид

 (2.4)
(2.4)

|
| Рис. 2.1. |
Задачу будем решать методом Фурье (методом разделения переменных). Частные, не равные тождественно нулю, решения уравнения (2.1), удовлетворяющие граничным условиям (2.3) будем искать в виде произведения двух функций, одна из которых зависит только от  , а другая – только от
, а другая – только от  , то есть
, то есть
 , (2.5)
, (2.5)
где  и
и  – дважды непрерывно-дифференцируемые функции своих аргументов, подлежащие определению. Функцию
– дважды непрерывно-дифференцируемые функции своих аргументов, подлежащие определению. Функцию 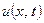 из (2.5) подставим в уравнение (2.1). Получим
из (2.5) подставим в уравнение (2.1). Получим
 .
.
Отсюда, разделяя переменные, находим
 . (2.6)
. (2.6)
Равенство (2.6), левая часть которого не зависит от  , а правая – от
, а правая – от  , возможно лишь в том случае, если обе его части не зависят ни от
, возможно лишь в том случае, если обе его части не зависят ни от  , ни от
, ни от  , то есть представляют собой одну и ту же постоянную, которую обозначим через
, то есть представляют собой одну и ту же постоянную, которую обозначим через 
 . Тогда
. Тогда
 .
.
Следовательно, получаем два уравнения относительно функций 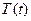 и
и  :
:
 (2.7)
(2.7)
и
 . (2.8)
. (2.8)
Удовлетворим  граничным условиям (2.3)
граничным условиям (2.3)
 ,
,  (2.9)
(2.9)
и найдём такие значения  , при которых существуют отличные от нуля решения уравнения (2.8). Для нахождения общего решения уравнения (2.8) составим характеристическое уравнение
, при которых существуют отличные от нуля решения уравнения (2.8). Для нахождения общего решения уравнения (2.8) составим характеристическое уравнение
 .
.
Корнями этого уравнения являются  , и, следовательно, общее решение уравнения (2.8) имеет вид
, и, следовательно, общее решение уравнения (2.8) имеет вид
|
|
|
 ,
,
 .
.
Подставим это решение в соотношения (2.9). Тогда

Решая систему, получим  ,
,  ;
; 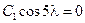 ,
,  , что возможно только в случае
, что возможно только в случае  ,
,  Отсюда собственные значения задачи Штурма – Лиувилля, то есть такие значения
Отсюда собственные значения задачи Штурма – Лиувилля, то есть такие значения  , при которых задача (2.8), (2.9) имеет нетривиальные решения, равны
, при которых задача (2.8), (2.9) имеет нетривиальные решения, равны  ,
,  Тогда решения этой задачи (собственные функции) имеют вид
Тогда решения этой задачи (собственные функции) имеют вид
 ,
, 
Найдём теперь общее решение уравнения (2.7) при  . Для этого составим характеристическое уравнение
. Для этого составим характеристическое уравнение
 .
.
Корнями этого уравнения будут  , и, следовательно, общее решение уравнения (2.7) имеет вид
, и, следовательно, общее решение уравнения (2.7) имеет вид
 .
.
Полагая в этом выражении  ,
,  , получаем
, получаем
 .
.
Тогда

 .
.
Каждому значению 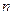 отвечают свои постоянные
отвечают свои постоянные  и
и  , поэтому пишем
, поэтому пишем 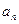 и
и  , а постоянную
, а постоянную  включаем в
включаем в 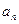 и
и  .
.
Так как уравнение (2.1) линейное и однородное, то функция
 (2.10)
(2.10)
является решением уравнения (2.1), удовлетворяющим граничным условиям (2.3).
Определим теперь  и
и  так, чтобы решение (2.10) удовлетворяло и начальным условиям (2.4), то есть
так, чтобы решение (2.10) удовлетворяло и начальным условиям (2.4), то есть
 ,
,  . (2.11)
. (2.11)
Функции  и
и  разлагаются в ряд Фурье в промежутке
разлагаются в ряд Фурье в промежутке  по косинусам, и тогда
по косинусам, и тогда
 . (2.12)
. (2.12)
 . (2.13)
. (2.13)
Подставляя выражения (2.4) для функций  и
и 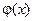 соответственно в (2.12) и (2.13), находим
соответственно в (2.12) и (2.13), находим




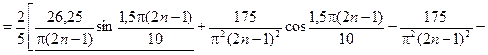

 ;
;


 .
.
Найденные значения 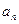 и
и  подставим в (2.10) и получим искомое решение в виде
подставим в (2.10) и получим искомое решение в виде

 .
.
Задача № 3. Методом Фурье найти решение  уравнения
уравнения
 , (3.1)
, (3.1)
удовлетворяющее начальному условию
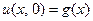 ,
,  (3.2)
(3.2)
и граничным условиям
 ,
,  ,
,  . (3.3)
. (3.3)
Вид функции  изображён на рисунке 3.1 (
изображён на рисунке 3.1 ( ;
;  ;
;  ;
;  ).
).
 Рис. 3.1.
Рис. 3.1.
|
Решение. Найдём аналитические выражения для функции 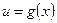 . Функция
. Функция  при
при  . В интервале
. В интервале  запишем
запишем 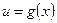 в виде уравнения прямой, проходящей через точку
в виде уравнения прямой, проходящей через точку 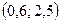 и имеющей угловой коэффициент
и имеющей угловой коэффициент  . Тогда в этом интервале
. Тогда в этом интервале
 .
.
С учётом полученных выражений начальное условие (3.2) запишем в виде
 (3.4)
(3.4)
Так как граничные условия не нулевые, то метод Фурье для решения задачи (3.1) – (3.3) не применим. Поэтому введём новую функцию
 , (3.5)
, (3.5)
где  и
и  – постоянные, которые надо определить так, чтобы
– постоянные, которые надо определить так, чтобы
 ,
, 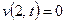 ,
,  . (3.6)
. (3.6)
|
|
|
Итак,
 , (3.7)
, (3.7)
 . (3.8)
. (3.8)
Из системы уравнений

имеем  ,
,  . Тогда
. Тогда
 . (3.9)
. (3.9)
Подставляя функцию  из (3.9) в уравнение (3.1), получим уравнение для функции
из (3.9) в уравнение (3.1), получим уравнение для функции  :
:
 , (3.10)
, (3.10)
а начальные и граничные условия примут вид:
 (3.11)
(3.11)
 ,
, 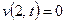 ,
,  . (3.12)
. (3.12)
Теперь для решения краевой задачи (3.10) – (3.12) можно применить метод Фурье. Пусть
 . (3.13)
. (3.13)
Подставляя (3.13) в (3.10) и разделяя переменные, получим
 ,
,  . (3.14)
. (3.14)
Из (3.14) получаем уравнения для определения  и
и  :
:
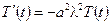 , (3.15)
, (3.15)
 . (3.16)
. (3.16)
Общие решения этих уравнений имеют вид
 , (3.17)
, (3.17)
 . (3.18)
. (3.18)
Для нахождения постоянных  и
и  воспользуемся граничными условиями (3.12). Функция
воспользуемся граничными условиями (3.12). Функция  , как следует из (3.12), удовлетворяет граничным условиям
, как следует из (3.12), удовлетворяет граничным условиям
 ,
,  . (3.19)
. (3.19)
Подставим (3.18) в граничные условия (3.19) Тогда
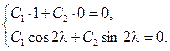
Решая эту систему уравнений и учитывая, что ищется ненулевое решение задачи Штурма – Лиувилля (3.16), (3.19), получим
 ,
,  ,
,  ,
,  ,
, 
Найденным собственным значениям  задачи соответствуют собственные функции
задачи соответствуют собственные функции
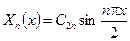 ,
, 
Общее решение (3.17) уравнения (3.15) при  примет вид
примет вид
 .
.
Тогда в соответствии с представлением решения  в виде (3.13) получим частные решения уравнения (3.10) в виде
в виде (3.13) получим частные решения уравнения (3.10) в виде
 ,
, 
Запишем теперь решение краевой задачи (3.10) – (3.12):
 , (3.20)
, (3.20)
где  – пока неизвестные постоянные, определяемые из начального условия (3.11). Полагая
– пока неизвестные постоянные, определяемые из начального условия (3.11). Полагая  в (3.20) и учитывая (3.11), получим
в (3.20) и учитывая (3.11), получим
 .
.
Отсюда найдём коэффициенты 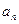 этого тригонометрического ряда Фурье:
этого тригонометрического ряда Фурье:



 .
.
Подставляя найденные значения 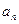 в (3.20) и учитывая (3.9), получим искомое решение в виде
в (3.20) и учитывая (3.9), получим искомое решение в виде
 .
.
Работу выполнил: дата, подпись.
|
|
|


