Аналогичным свойством обладают точки А1, В1, С1, D1 пересечения прямых МА, МВ, МС, MD с какой-нибудь прямой, параллельной прямой АD.

Через точки А, В, С, D, лежащие на одной прямой, проведем 4 параллельные прямые. Пусть А1, В1, С1, D1 – точки пересечения этих прямых с какой-нибудь другой прямой. Тогда, если А, В, С, D – гармоническая четверка, то А1, В1, С1, D1 также гармоническая четверка.

Аналогичным свойством обладают точки А1, В1, С1, D1 пересечения прямых МА, МВ, МС, MD с какой-нибудь прямой, параллельной прямой АD.

 

15. Построение четвертой гармонической.

Четвертка точек при этом образует т.н. гармоническую четверку – см.[1],[6],[11]. На рисунке ниже указан способ построения четвертой гармонической: из точки проводим произвольную прямую, отмечаем точки пересечения ее с прямыми (СА) и (ВА) – точк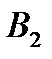и и , потом строим точку Р пересечения и 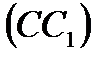, и, наконец – точку пересечения (АР) и (ВС).

16. Полный четырехвершинник и полный четырехсторонник.

Полным четырехвершинником называется фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой и шести прямых проходящих через эти точки (рис. 3). Точки А, В, С, D называются вершинами, прямые АВ, CD, АС, ВD, ВС, AD – сторонами полного четырехвершинника. Стороны, не имеющие общей вершины, называются противоположными; точки пересечения противоположных сторон P, Q, R называются диагональными точками.

Фигура, двойственная четырехвершиннику, называется четырехсторонником – совокупность четырех прямых, лежащих в одной плоскости, из которых никакие три не принадлежат одной точке.

17. Применение свойств полного четырехвершинника к построению гармонических четверок точек

18. Проективные преобразования проективной прямой.

Проективное преобразование — это преобразование проективной плоскости, переводящее прямые в прямыe.

Пусть l ₁ и l ₂ - две прямые на плоскости, O - точка, не лежащая ни на одной из этих прямых. Центральным проектированием прямой l ₁ на прямую l ₂ с центром O называют отображение, которое точке A ₁ прямой l ₁ ставит в соответствие точку пересечения прямой OA ₁ с прямой l ₂.

Пусть l ₁ и l ₂ - две прямые на плоскости, l - прямая, не параллельная ни одной из этих прямых. Параллельным проектированием прямой l ₁ на прямую l ₂ вдоль прямой l называют отображение, которое точке A ₁ прямой l ₁ ставит в соответствие точку пересечения прямой l ₂ с прямой, проходящей через точку A ₁ параллельно прямой l.

Отображение P прямой a на прямую b называют проективным, если оно является композицией центральных или параллельных проектирований, т. е. если существуют прямые a ₀ = a, a ₁, ¼, a_n = b и отображения P_i прямых a_i на a_{i + 1}, каждое из которых является либо центральным, либо параллельным проектированием, причем P является композицией преобразований P_i. В случае, когда прямая b совпадает с прямой a, отображение P называют проективным преобразованием прямой a.

19. Проективные преобразования проективной плоскости.

Определение. Пусть a₁ и a₂ - две плоскости в пространстве, O - точка, не лежащая ни на одной из этих плоскостей. Центральным проектированием плоскости a₁ на плоскость a₂ с центром O называют отображение, которое точке A ₁ плоскости a₁ ставит в соответствие точку пересечения прямой OA ₁ с плоскостью a₂.

Прямую, на которой не определено центральное проектирование, называют исключительной прямой данной проекции.

Отображение P плоскости a на плоскость b называют проективным, если оно является композицией центральных проектирований и аффинных преобразований, т. е. если существуют плоскости a₀ = a, a₁, ¼, a _n = b и отображения P_i плоскостей a _i на a _{i + 1}, каждое из которых является либо центральным проектированием, либо аффинным преобразованием, причем P является композицией преобразований P_i. В случае, когда плоскость a совпадает с плоскостью b, отображение P называют проективным преобразованием плоскости a. Прообраз бесконечно удаленной прямой мы будем называть исключительной прямой данного проективного преобразования

20. Группа проективных преобразований. Предмет проективной геометрии.

 

 

21. Линии второго порядка на проективной прямой.

Кривой второго порядка на проективной плоскости называется множество точек, однородной координаты которой удовлетворяют уравнению вида:

22. Полюс и поляра. Свойства.

Поляра точки P относительно невырожденной кривой второго порядка — множество точек N, гармонически сопряжённых с точкой P относительно точек M ₁ и M ₂ пересечения кривой 2-го порядка секущими, проходящими через точку P.

Поляра является прямой линией. Точку P называют полюсом поляры. Всякая невырожденная линия 2-го порядка определяет биекцию точек проективной плоскости и множества её прямых — поляритет или полярное преобразование.

Свойства:

• Если точка P лежит «вне» линии 2-го порядка (то есть через точку P можно провести две касательные к линии), то поляра проходит через точки касания данной линии с прямыми, проведёнными через точку P.
• Если точка P лежит на кривой 2-го порядка, то поляра является прямой, касательной к данной кривой в этой точке.
• Если поляра точки P проходит через точку Q, то поляра точки Q проходит через точку Р.

 

23. Приведение общего уравнения линии второго порядка к каноническому виду.

24. Классификация линий второго порядка на проективной плоскости.

Классификация линий второго порядка

№	Название	Уравнение	Ранг
	Овальная линия
	Нулевая линия
	Пара прямых
	Пара мнимых прямых
	Пара совпавших прямых

 

25. Бесконечно-удаленные элементы квадрики

Рассмотрим в евклидовой плоскости a ее параллельные прямые а и а'(рис., 1)и прямую b, пересекающую их соответственно в точках М и М'. Будем поворачивать прямую b вокруг точки М' в направлении, указанном на рис. стрелкой, до совпадения с прямой а '. Очевидно, по мере приближения прямой b к a' точка М пересечения прямых a и b будет удаляться в бесконечность. Этот процесс достаточно отчетливо поясняет часто употребляемое выражение: "параллельные прямые пересекаются в бесконечно удалённой точке".

Указанные наглядные соображения лежат в основе интерпретации двумерной проективной геометрии на евклидовой плоскости a. Для этой цели плоскость a пополняется бесконечно удалёнными точками и одной бесконечно удалённой прямой следующим образом. Уславливаются рассматривать параллельные прямые как пересекающиеся в бесконечно удалённой точке. Тогда прямая а', параллельная прямой а (рис., 2), пересекается с ней в некоторой точке, но только эта точка не является обыкновенной, а представляет собой новый объект - бесконечно удалённую точку прямой а. Уславливаются, что все прямые, параллельные прямой а, имеют одну общую бесконечно удалённую точку А, а бесконечно удалённые точки непараллельных прямых считаются различными. Т. о., евклидова плоскость пополняется бесконечным числом бесконечно удалённых точек. Совокупность всех этих бесконечно удалённых точек плоскости се называют бесконечно удалённой прямой.

Плоскость a, пополненная т. о. бесконечно удалёнными точками и бесконечно удалённой прямой, представляет собой т. н. проективную плоскость. Её свойства отличаются от свойств евклидовой плоскости (например, на проективной плоскости пересекаются любые две прямые).
Евклидову плоскость можно пополнять Б. у. э. и др. способами. Так, при изображении комплексных чисел на евклидовой плоскости, последняя пополняется одной бесконечно удалённой точкой, которая отвечает одному бесконечно большому комплексному числу.

26. Касательная к линии квадрики

27. Геометрия проективной плоскости с фиксированной прямой

Поделиться:

Воспользуйтесь поиском по сайту: