 |
Прямая и плоскость в пространстве
|
|
|
|
ТЕОРИЯ
1. Уравнение прямой в 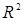 .
.
2. Общее уравнение прямой. Векторная форма записи.
3. Уравнение в отрезках.
4. Уравнение прямой, проходящей через две точки.
5. Нормальное уравнение прямой.
6. Расстояние от точки до прямой.
7. Уравнение прямой с угловым коэффициентом.
8. Уравнение прямой проходящей через заданную точку в заданном направлении.
9. Каноническое уравнение прямой.
10. Параметрическое уравнение прямой.
11. Задачи на прямую в плоскости (треугольник, параллелограмм, трапеция, четырехугольник, квадрат, проекция точки на прямую)
12. Взаимное расположение двух прямых. Угол между двумя прямыми.
Условие параллельности и перпендикулярности двух прямых на плоскости.
13. Уравнение прямой в  .
.
14. Общее уравнение прямой. Векторная форма записи.
15. Уравнение в отрезках.
16. Уравнение прямой, проходящей через две точки.
17. Нормальное уравнение прямой.
18. Расстояние от точки до прямой.
19. Уравнение прямой проходящей через заданную точку в заданном направлении.
20. Каноническое уравнение прямой.
21. Параметрическое уравнение прямой.
22. Задачи на прямую в пространстве. Взаимное расположение двух прямых в пространстве.
23. Угол между двумя прямыми.
24. Условие перпендикулярности и параллельности двух прямых в пространстве.
2. Уравнение плоскости.
25. Общее уравнение плоскости.
26. Векторная форма записи.
27. Уравнение плоскости проходящей через заданную точки с заданным нормальным вектором.
28. Уравнение плоскости проходящей через три точки.
29. Условие принадлежности четырех точек в пространстве плоскости.
30. Нормальное уравнение плоскости.
31. Расстояние от точки до плоскости.
32. Взаимное расположение двух плоскостей. Угол между двумя плоскостями.
|
|
|
33.Условие параллельности двух плоскостей.
34.Условие перпендикулярности двух плоскостей.
35. Задачи на взаимное расположение точки и плоскости в пространстве.
36. Задачи на взаимное расположение точки и прямой в пространстве.
37. Задачи на взаимное расположение прямой и плоскости в пространстве.
38. Уравнение прямой, как пересечение двух плоскостей.
39. Кривые второго порядка на плоскости.
40. Эллипс, каноническое уравнение, геометрические характеристики и свойства.
41. Гипербола, каноническое уравнение, геометрические характеристики и свойства.
42. Парабола, каноническое уравнения, геометрические характеристики и свойства.
43. Геометрические свойства кривых второго порядка.
44. Приведение общего уравнения кривой второго порядка к каноническому виду.
ЗАДАЧИ
Прямая на плоскости
1. Определить острый угол между высотой и медианой треугольника АВС, проведенных из вершины А, если координаты вершин треугольника заданы
А(-2,3), В(5,7), С(-3,-2). А(-1,1), В(6,5), С(-2,-4). А(-3,5), В(4,9), С(-4,0).
2. В треугольнике АВС найти координаты центра тяжести, длину и уравнение медианы ВК, если координаты вершин треугольника заданы
А(5,6), В(-2,2), С(-3,-3). А(6,4), В(-1,0), С(-2,-5). А(4,8), В(-3,4), С(-4,-1).
3. В треугольнике АВС известны координаты вершин. Составить уравнение высоты ВК и определить острый угол между этой высотой и стороной ВС:
А(-5,-2), В(-4,3), С(3,7). А(-4,-4), В(-3,1), С(4,5). А(-6,0), В(-5,5), С(2,9).
4. В треугольнике АВС известны координаты вершин. Найти угол между сторонами АВ и АС и составить уравнение средней линии, параллельной стороне ВС:
А(2,-5), В(1,-3), С(4,1). А(3,-7), В(2,-5), С(5,-1). А(1,-3), В(0,-1), С(3,3).
5. В треугольнике АВС известны координаты вершин. Найти точку пересечения высоты АD и медианы ВК:
А(6,2), В(30,-5), С(12,0). А(7,0), В(31,-7), С(13,-2). А(5,4), В(29,-3), С(11,2).
6. Точки А и В с ординатами 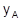 и
и 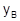 лежат на некоторой прямой L. Координаты точки С известны. Составить уравнение высоты АD треугольника АВС, найти ее длину и величину угла ВАD
лежат на некоторой прямой L. Координаты точки С известны. Составить уравнение высоты АD треугольника АВС, найти ее длину и величину угла ВАD
|
|
|
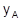 =6,
=6, 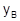 =-2, L: 2x+y-6=0, С(0,0).
=-2, L: 2x+y-6=0, С(0,0).
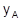 =4,
=4, 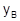 =-4, L: 2x+y-6=0, С(1,-2).
=-4, L: 2x+y-6=0, С(1,-2).
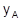 =8,
=8, 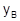 =0, L: 2x+y-6=0, С(-1,2).
=0, L: 2x+y-6=0, С(-1,2).
7. В треугольнике АВС известны координаты вершин. Составить уравнение медианы и высоты, проведенных из вершины А, найти угол между ними:
А(-3,1), В(2,0), С(1,-4). А(-2,-1), В(3,-2), С(2,-6). А(-4,3), В(1,2), С(0,-2).
8. Составить уравнение сторон треугольника АВС, если известны координаты двух его вершин А и В и точки пересечения его высот М:
А(-3,3), В(5,-1), М(4,3). А(-2,1), В(6,3), М(5,1). А(-4,5), В(4,1), М(3,5).
9. В треугольнике АВС известны координаты двух его вершин А и В и точки пересечения его медиан Е. Составить уравнение высоты треугольника проведенной из вершины С:
А(2,-2), В(3,-1), Е(1,0). А(3,-4), В(4,-3), Е(2,-2). А(1,0), В(2,1), Е(0,2).
10. Найти на прямой L точку М, равноудаленную от точек А и В а также угол АМВ:
А(-1,2), В(1,4), L: 4x+3y-12=0.
А(0,-4), В(2,2), L: 4x+3y-10=0.
А(-2,0), В(0,6), L: 4x+3y-14=0.
11. Найти площадь ромба и координаты его вершин, если одна из его сторон и диагоналей лежат соответственно на прямых L1 и L2, а длина данной диагонали равна 12. Сколько решений имеет задача?
L1: 2x-y+2=0 L2: x-3=0
L1: 2x-y-2=0 L2: x-4=0
L1: 2x-y+6=0 L2: x-2=0
12. Составить уравнение сторон ромба АВСD и найти его площадь, если известны уравнения сторон АВ и ВС и координаты вершины D:
АВ: 2x+y-2=0 ВС: 2x-y+2=0 D(3,4)
АВ: 2x+y-2=0 ВС: 2x-y-2=0 D(4,2)
АВ: 2x+y+2=0 ВС: 2x-y+6=0 D(2,6)
13. Найти площадь и координаты вершин ромба АВСD, если известны уравнения сторон АВ и DС и уравнение диагонали АС:
АВ: x+2y-4=0 DС: x+2y-10=0 АС:x-y+2=0
АВ: x+2y-1=0 DС: x+2y-7=0 АС:x-y-1=0
АВ: x+2y-7=0 DС: x+2y-13=0 АС:x-y+5=0
14. Составить уравнение сторон квадрата АВСD, если известны координаты вершины А и уравнения диагоналей ВD и АС:
А(-1,8), ВD: 4x-5y+3=0 АС: 5x+4y-27=0
А(0,6), ВD: 4x-5y-11=0 АС: 5x+4y-24=0
А(-2,10), ВD: 4x-5y+17=0 АС: 5x+4y-30=0
15. В квадрате АВСDзаданы вершина А и точка пересечения диагоналей К. Составить уравнение сторон и найти координаты остальных вершин:
А(2,-1), К(-1,-4).
А(3,-3), К(0,-6).
А(1,1), К(-3,-2).
16. Известны координаты вершин четырехугольника АВСD. Доказать, что АВСD трапеция. Найти ее площадь.
А(3,6), В(5,2), С(-1,-3), D(-5,5)
А(4,4), В(6,0), С(0,-5), D(-4,3)
А(2,8), В(4,4), С(-2,-1), D(-6,7)
17. Найти координаты вершин и уравнения диагоналей квадрата АВСD, если известно уравнение стороны АВ и координаты точки пересечения диагоналей Е:
Е(4,4), АВ: x+y-5=0
Е(5,2), АВ: x+y-4=0
|
|
|
Е(3,6), АВ: x+y-6=0
18. В параллелограмме АВСD известны уравнения сторон АD и АВ и координаты точки пересечения диагоналей Е. Составить уравнение двух других сторон и диагоналей параллелограмма:
АD: x-y-2=0 АВ: x-5y+6=0 Е(0,0)
АD: x-y-5=0 АВ: x-5y-5=0 Е(1,-2)
АD: x-y+1=0 АВ: x-5y+17=0 Е(-1,2)
19. Даны две противоположные вершины квадрата А и С. Найти координаты двух других вершин и уравнения сторон квадрата:
А(0,1), С(2,3).
А(1,-1), С(3,1).
А(-1,3), С(1,5).
20. В равнобочной трапеции АВСD известны координаты трех вершин А,В и С. Найти координаты вершины D и острый угол, если стороны ВС и АD параллельны:
А(1,2), В(3,4), С(5,1).
А(2,0), В(4,2), С(6,-1).
А(0,4), В(2,6), С(4,3).
Кривая на плоскости
Установить, какая линия определена уравнением, и построить эту линию:
1. 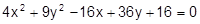 16.
16. 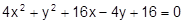
2.  17.
17. 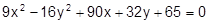
3. 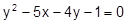 18.
18. 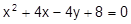
4. 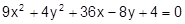 19.
19. 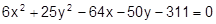
5. 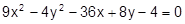 20.
20. 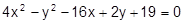
6.  21.
21. 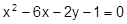
7. 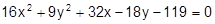 22.
22. 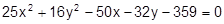
8. 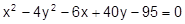 23.
23. 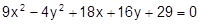
9. 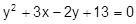 24.
24. 
10. 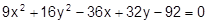 25.
25. 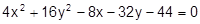
11.  26.
26. 
12. 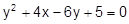 27.
27. 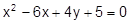
13.  28.
28. 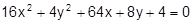
14.  29.
29. 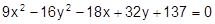
15.  30.
30. 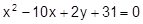
Прямая и плоскость в пространстве
1.Найти длину высоты DH, составить ее уравнение, найти координаты точки H пирамиды с вершинами в точках А(-1,0,0), В(1,-2,-1), С(-1,6,2), D(-1,0,2).
2.Известны координаты вершин треугольника АВС: А(-1,0,0), В(1,-2,-1), С(-1,6,1).
Составить уравнение высоты АК треугольника АВС, найти длину высоты АК, найти координаты точки К.
3.Известны координаты вершин треугольника АВС: А(-1,0,0), В(1,-2,-1), С(-1,6,1).
Составить уравнение биссектрисы АL треугольника АВС, найти координаты точки L.
4. Составить уравнение плоскости проходящей через точку М(0,1,2) и прямую 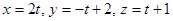
5. Составить уравнение проекции прямой 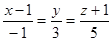 на плоскость
на плоскость  .
.
6.Найти координаты проекции точки А(7,1,1) на плоскость 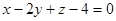 .
.
7.Найти расстояние от точки пересечения прямой 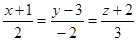 и плоскости
и плоскости
 до плоскости
до плоскости  .
.
8. Найти расстояние между сторонами AD и BC пирамиды с вершинами в точках
А(-1,0,0), В(1,-2,-1), С(-1,6,2), D(-1,0,2).
9. Написать уравнение общего перпендикуляра между сторонами AD и BC пирамиды с вершинами в точках А(-1,0,0), В(1,-2,-1), С(-1,6,2), D(-1,0,2).
10.Найти угол между прямыми 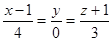 и
и 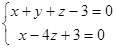 .
.
11. Найти координаты точки пересечения прямой 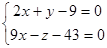 и плоскостью
и плоскостью
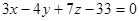 .
.
12. Составить уравнение прямой, проходящей через точку А, перпендикулярно к плоскости, которая проходит через точки А,В,С:
А(1,4,1), В(2,3,-1), С(0,-1,0).
|
|
|
А(0,1,1), В(2,7,1), С(1,0,-1).
А(1,6,2), В(-1,0,2), С(1,2,0).
А(1,2,0), В(2,5,0), С(0,3,2).
А(0,-1,0), В(2,1,-2), С(1,4,1).
А(0,3,2), В(1,0,-1), С(1,6,2).
13. Составить уравнение плоскости, проходящей через точки А и В параллельно оси Oz:
А(-1,0,2), В(3,2,5).
А(1,1,-4), В(-3,-1,2).
А(5,3,1), В(1,1,2).
А(-1,0,5), В(-5,-2,1).
А(3,2,-1), В(5,3,-2).
А(-3,-2,0), В(7,4,1).
14. Через точку А провести плоскость параллельно прямым 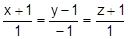 ,
, 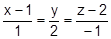 :
:
А(3,1,2), А(4,0,3), А(1,0,2), А(0,1,1)
А(5,2,2), А(-2,0,1)
15. Составить уравнение плоскости, проходящей через точку А перпендикулярно плоскостям 2x-y+2z=0, 3x-2y+6z+1=0:
А(2,-1,6), А(-1,3,-3), А(1,4,3), А(-1,0,6), А(2,-5,6), А(3,-8,9)
16. Составить уравнение плоскости, проходящей через точки А и В перпендикулярно плоскости x+y+z-2=0
А(0,0,-2), В(2,2,1)
А(0,2,3), В(-2,2,1)
А(1,0,-2), В(-1,0,0)
А(0,1,1), В(2,1,1)
А(-1,1,2), В(2,3,3)
А(1,2,2), В(1,1,0)
17.Найти точку пересечения плоскости XoY и прямой, проходящей через точки А и В:
А(5,0,5), В(2,6,1)
А(1,2,3), В(-11,8,-3)
А(-1,3,2), В(9,-2,7)
А(3,1,4), В(-7,6,1)
А(-9,7,2), В(-11,2,3)
А(7,-1,6), В(11,-3,8)
18.Найти уравнение медианы треугольника АВС, проведенной из вершины А и угол АВС
А(-2,1,3), В(2,6,1), С(0,2,-1).
А(-1,2,2), В(3,7,0), С(1,3,-2).
А(0,3,1), В(0,4,3), С(-2,0,1).
А(1,4,0), В(1,8,0), С(3,2,-2).
А(2,5,-1), В(3,3,1), С(-1,5,-1).
А(3,6,-2), В(0,3,3), С(-2,1,1).
19. Написать параметрическое и каноническое уравнение прямой, заданной как пересечение двух плоскостей:
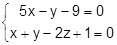
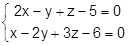
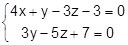
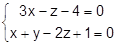
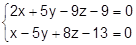
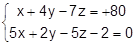
20. При каком значении D прямая  пересекает:
пересекает:
ось OX
ось OY
ось OZ
21. При каком значении  прямая
прямая  параллельна:
параллельна:
плоскости YOZ
плоскости XOZ
плоскости XOY
22. Через точку А провести прямую, параллельную двум плоскостям
А(3,1,0), 3x+5y-z-5=0, x+2y+1=0
А(7,-1,2), x+y-z+3=0, 2x+y-3z+8=0
А(5,0,1), 2x+3y-z+4=0, x+4y+2z-3=0
А(-3,4,3), 3x+4y-2z+7=0, x-2z+5=0
А(-1,3,-2), 2x+5y+z=0, y+z-2=0
А(1,2,-1), 2x+3y-z+4=0, x+3y+z-1=0
23. Найти проекцию точки А на прямую, заданную как пересечение двух плоскостей:
А(-2,3,1), 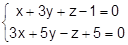 А(-3,2,2),
А(-3,2,2),  А(-1,1,-3),
А(-1,1,-3), 
А(-2,1,-1),  А(-1,5,1),
А(-1,5,1),  А(-3,3,3),
А(-3,3,3), 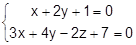
24. Составить уравнение перпендикуляра, опущенного из точки А на прямую
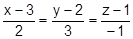
А(-1,-1,-2),
А(2,-1,4),
А(-1,0,1),
А(2,-2,1),
А(0,-1,0),
А(0,0,3)
25. Найти проекцию точки А на плоскость
А(3,2,4), 2x+y+3z-6=0
А(1,3,0), 2y-z-1=0
А(1,1,3), z-1=0
А(3,0,-2), 2x-y-3z+2=0
А(-2,1,2), 3x-z-2=0
А(3,2,-3), 2x+y-4z+1=0
26. Составить уравнение высоты, опущенной из вершины А треугольной пирамиды АВСD на основание АВС:
А(1,1,6), В(1,2,7), С(3,3,6), D(5,2,6)
А(1,0,7), В(1,-1,4), С(2,4,8), D(2,5,3)
А(1,0,5), В(1,-4,1), С(1,-2,3), D(6,1,7)
А(0,0,6), В(1,3,8), С(3,5,8), D(3,4,4)
А(3,4,7), В(-1,1,8), С(1,-3,2), D(1,6,2)
А(2,3,7), В(2,2,6), С(-1,2,9), D(7,0,8)
1. Теория. Прямая на плоскости. Кривая второго порядка на плоскости.
2. Теория. Прямая или плоскость в пространстве
3. Задача на прямую в плоскости.
4. Задача на прямую или плоскость в пространстве
5. Задача. Привести к каноническому виду кривую второго порядка.
|
|
|


