Типы моделей управления доступом.

1. Модель конечного автомата описывает систему как абстрактную математическую машину. В этой модели переменные состояния представляют состояния машины, а функции перехода описывают способ изменения переменных.
   Модель управления доступом имеет дело только с наиболее существенными переменными состояниями, влияющими на безопасность и потому намного проще, чем полная модель конечного автомата для данной системы.
2. Модель матрицы доступа (частный случай реализации модели машины состояний).
   Состояния безопасности системы представлены в виде таблицы, содержащей по одной строке для каждого субъекта системы и по одной колонке для каждого субъекта и объекта.
   Каждое пересечение в массиве определяет режим доступа данного субъекта к каждому объекту или другому субъекту системы.

Субъекты	Объекты	Субъекты
	чтение, запись	чтение	-	-	запись	запись
	чтение	чтение, исполнение	чтение, запись	пересылка	-	-
	-	чтение, запись	исполнение	пересылка	запись	-

1. Второй составляющей модели матрицы доступа является набор функций перехода, описывающих способ изменения матрицы доступа. Более часто матрица доступа используется не как самостоятельная модель управления доступом, а в качестве одной из нескольких переменных состояния в более общей модели конечного автомата.
   Другим способом описания управления доступом является модель, выраженная в терминах меток безопасности, приписываемых субъектом и объектом системы.
   Режим доступа, которым обладает субъект по отношению к объекту, определяется при сравнении их меток безопасности вместо того, чтобы искать соответствующие пересечения строки и столбца в матрице доступа.
   Модель может использовать как матрицу доступа, так и атрибуты безопасности.
2. Вариантом модели управления доступом является модель информационных потоков, которая предназначена для анализа потоков информации из одного объекта в другой на основании их меток безопасности.
3. Модель интерференции, в которой субъекты, работающие в различных доменах, защищены от взаимовлияния друг на друга, любым способом, нарушающим свойства безопасности системы.
   Характеристики модели безопасности.
   Модель является лишь формулировкой математических терминов, свойств безопасности, которым должна удовлетворять система. Не существует формального способа, с помощью которого можно доказать, что формальная модель управления доступом соответствует правилам управления доступом, принятым в данной системе.
   С другой стороны, модель может иметь ряд характеристик, назначение которых не столь очевидно. Поскольку модель должна стремиться к математическому совершенству в определении свойств, составляющих политику безопасности, это часто влечет за собой включение ограничений или дополнительных свойств, присутствие которых ранее не предусматривалось.
   Описание модели управления доступом (МУД) к системе как конечного автомата.
   Представление МУД как конечного автомата получило предпочтение из-за того, что они представляют компьютерную систему способом, имитирующим работу ОС и аппаратуры. Переменное состояние является абстракцией для каждого бита и байта в системе, изменяющихся по мере работы в системе. Функция перехода из состояния в состояние - это абстракция обращений к ОС, явно описывающая то, как состояние может (или не может) измениться.
   МУД работает не со всеми переменными состояния и функциями системы.
   Выбор для моделирования переменных и функций, имеющих отношение к безопасности, остается за разработчиком модели.
   Разработка моделей управления доступом включает в себя определение элементов моделей (переменных, функций, правил и т.д.), а также безопасного начального состояния.
   Математически доказывается, что начальное состояние безопасно, и что все функции безопасны, после чего, путем математической индукции делается вывод о том, что если система первоначально находилась в безопасном состоянии, система остается в безопасном состоянии независимо от того, какие функции, и в каком порядке будут выполнены.
   Таким образом, в разработке МУД можно выделить следующие шаги:
1. Определение переменных состояний, имеющих отношение к безопасности. Обычно переменные состояния представляют объекты и субъекты системы, их атрибуты безопасности и права доступа между субъектами и объектами.
2. Определение условий для безопасного состояния. Это определение является выражением отношений между значениями переменных состояния, истинность которого должна обеспечиваться при переходах состояния.
3. Определение функций переходов из состояния в состояние. Эти функции описывают допустимые способы изменения переменных состояния. Они также называются правилами изменения доступа, поскольку их цель состоит в указании изменений, которые может производить система, а вовсе не в определении всех возможных изменений. Правила могут быть очень общими и могут допускать наличие функций, которых нет в реальной системе, однако система не может менять переменные состояния каким-либо способом, который не допускается функциями.
   Можно выделить несколько характерных черт функций перехода:
• назначение функции.
• определение взаимосвязи между переменными, предыдущим и новым состояниями.
• функция не задает какого-либо конкретного порядка в выполнении алгоритма операции.
• функция элементарна.
4. Доказывается, что функции обеспечивают сохранение безопасного состояния.
   Чтобы удостовериться в том, что модель является безопасной, необходимо для каждой функции перехода доказать, что если система находится в безопасном состоянии до начала выполнения функции перехода, то система останется в этом состоянии по ее завершении.
5. Определение начального состояния.
   Математически, начальное состояние выражается как множество начальных значений всех переменных состояний системы. Простейшим начальным состоянием является состояние вообще без каких-либо субъектов и объектов.
   При этом нет необходимости определять начальные значения каких-либо других переменных состояний, поскольку состояние будет безопасным независимо от их значения. Более реалистичное безопасное начальное состояние предполагает наличие некоторого начального множества субъектов и объектов.
6. Доказывается, что начальное состояние безопасно в соответствии с определением.
4. Списки управления доступом к объектам.
   В данной модели полномочия доступа определяются в виде списка картежей для всех субъектов, имеющих доступ к данному объекту.

Объекты	Списки картежей	Методы доступа
O1	S1	r (чтение)	w (запись)	c (копирование)
O2	S2	w	r	x (удаление)

1. Достоинства данной модели:

• экономия памяти
• удобство получения сведений о субъектах, имеющих доступ к данному объекту

Недостатки:

• неудобство получения сведений об объектах, к которым имеет доступ данный субъект
• неудобство отслеживания ограничений и зависимостей по наследованию полномочий субъекта
1. Списки полномочий субъектов.

Списки картежей	Объекты	Методы доступа
S1	O1	r (чтение)	w (запись)	c (копирование)
S2	O2	w	r	x (удаление)

1. В данной модели полномочия доступа субъекта представляются в виде списка картежей для всех объектов, в которых он имеет доступ.
   Профиль субъекта используется для отслеживания событий аудита в ОС Microsoft и MSNT.
   Достоинства модели:
• экономия памяти
• удобство получения сведений об объектах, к которым имеет доступ данный субъект

Недостатки:

• неудобство получения сведений о субъектах, которые имеют доступ данному объекту
1. Атрибутная схема.
   Атрибутные способы задания матрицы доступа основаны на присвоении субъектом и объектом определенных меток (содержащих значения атрибутов). Такая схема используется в ОС семейства Unix.
   Матрица задана в неявном виде.
   Вычисление уровня доступа субъекта к объекту происходит динамически.
   Существуют также многоуровневые модели управления доступом.

• 3. Криптография
• 3.1 Алгоритмы и ключи
• 3.2 Криптоанализ

Тема 3: Криптография

Открытым текстом называется исходное сообщение.
Изменение вида сообщения так, чтобы спрятать его суть называется шифрованием.
Шифрованное сообщение называется шифротекстом.
Процесс преобразования шифротекста в открытый текст называется дешифрованием.
Искусство и наука безопасных сообщений называется криптографией.
Криптоаналитиками называются те, кто постоянно использует криптоанализ (искусство и наука взламывать шифротекст).
Криптография часто используется и для других целей:

1. Проверка подлинности. Получатель сообщения может проверить его источник. Злоумышленник не сможет замаскироваться под кого-либо.
2. Целостность. Получатель сообщения может проверить не было ли сообщение изменено в процессе доставки.
3. Неотрицание авторства. Отправитель не сможет ложно отрицать отправку сообщения.

Алгоритмы и ключи.

 

Криптографический алгоритм, также называемый шифром, представляет собой математическую функцию, используемую для шифрования и дешифрования. Обычно это две связанные функции: одна для шифрования, другая - для дешифрования.

Основные требования, предъявляемые к методам защитного преобразования:

1. Применяемый метод должен быть достаточно устойчив к попыткам раскрыть исходный текст имея только зашифрованный текст.
2. Объем ключа не должен затруднять его запоминание и пересылку.
3. Алгоритм преобразования информации и ключ, используемый для шифрования и дешифрования не должны быть очень сложными. Затраты на защитные преобразования должны быть приемлемы при заданном уровне сохранности информации.
4. Ошибки в шифровании не должны вызывать потерю информации. Из-за появления ошибок передачи шифрованного сообщения по каналам связи не должна исключаться возможность надежной расшифровки текста на приемном конце.
5. Длина зашифрованного текста не должна превышать длину исходного текста.
6. Необходимые временные и стоимостные ресурсы на шифрование и дешифрование информации определяются требуемой степенью защиты информации.

Множество современных методов защитных преобразований можно классифицировать на 4 большие группы:

1. Перестановки.
2. Замены.
3. Аддитивные.
4. Комбинированные.

Методы перестановки и подстановки обычно характеризуются короткой длиной ключа, а надежность их защиты определяется сложностью алгоритмов преобразования.

Для аддитивных методов характерны простые алгоритмы преобразования, а их надежность основана на увеличении длины ключа.

Все перечисленные методы относятся к симметричному шифрованию (для шифрования и дешифрования используется один и тот же ключ).

Асимметричное - один ключ для шифрования (открытый), другой - для дешифрования (закрытый).

1. Метод перестановки.

Суть состоит в том, что входной поток исходного текста делится на блоки, в каждом из которых выполняется перестановка символов.

Простейшим примером перестановки является запись исходного текста по строкам некоторой матрицы и чтение его по столбцам этой матрицы. Последовательность заполнения строк и чтение столбцов может быть любой и задается ключом.

Для матрицы размером 8х8 возможно 1,6*10⁹ ключей.

Для методов перестановки характерны простота алгоритма, возможность программной реализации и низкий уровень защиты.

Т.к. при большой длине исходного текста в шифрованном тексте проявляются статистические закономерности ключа, - это позволяет его быстро раскрыть.

Другой недостаток этого метода - легкое раскрытие, если удается направить в систему для шифрования несколько специально подобранных сообщений. Если длина блока в исходном тексте равна k символам, то для раскрытия ключа достаточно пропустить через шифрованную систему (k-1) блоков исходного текста, в которых все символы кроме одного одинаковы.

1. Метод замены (подстановки).

Заключается в том, что символы исходного текста, записанные в одном алфавите, заменяются символами другого алфавита в соответствии с принятым ключом преобразования.

Одним из простейших методов является прямая замена исходных символов их эквивалентом из вектора замен.

Для очередного символа исходного текста отыскивается его местоположение в исходном алфавите. Эквивалент из вектора замены выбирается как отстоящий на полученное смещение от начала алфавита.

При дешифровании поиск производится в векторе замен, а эквивалент выбирается из алфавита. Полученный таким образом текст имеет низкий уровень защиты.

Более стойкой отношении раскрытия является схема шифрования, основанная на использовании таблицы Вижинера: таблица представляет собой квадратную матрицу с числом элементов k, где k - количество символов в алфавите. В первой строке матрицы записываются буквы в порядке очередности их в алфавите, во второй - та же последовательность букв, но со сдвигом влево на одну позицию, в третьей - со сдвигом на 2 позиции и т.д. Освободившиеся места справа заполняются вытесненными влево буквами, записанными в естественной последовательности.

Для шифрования текста устанавливается ключ, представляющий собой некоторое слово или набор букв. Далее, из полной матрицы выбирается подматрица шифрования, включающая, например, первую строку и строку матрицы, начальные буквы которой являются последовательной буквой ключа.

Пример:
Ключ - МОРЕ
АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ

МНОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВГДЕЁЖЗИЙКЛ
ОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВГДЕЁЖЗИЙКЛМН
РСТУФХЦЧШЩЪЫЬЭЮЯАБВГДЕЁЖЗИЙКЛМНОП
ЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВГД

Исходный текст:
ЗАЩИТА ИНФОРМАЦИИ
МОРЕМО РЕМОРЕМОРЕ
Зашифрованный текст:
УОИОЭО ШТЯЫЯСМГШО

Процесс шифрования включает следующую последовательность действий:

1. Под каждой буквой шифруемого текста записываются буквы ключа, повторяющие ключ требуемой число раз.
2. Шифруемый текст по подматрице заменяется буквами, расположенными на пересечении линий, соединяющих буквы текста первой строки подматрицы и буквы ключа, находящиеся под ней.

Пример:
Ключ - ОКНО
АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ

ОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВГДЕЁЖЗИЙКЛМН
КЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВГДЕЁЖЗИЙ
НОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВГДЕЁЖЗИЙКЛМ
ОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВГДЕЁЖЗИЙКЛМН

ЗАЩИТА ИНФОРМАЦИИ
ОКНООК НООКНООКНО
ЦКЁЧАК ЦЫВШЭЪОАЦЧ

Расшифровка текста выполняется в следующей последовательности:

1. Над буквами шифрованного текста последовательно записываются буквы ключа.
2. В строке подматрицы таблицы Вижинера для каждой буквы ключа отыскивается буква, соответствующая знаку шифрованного текста. Находящаяся над ней буква первой строки и будет знаком расшифрованного текста.
3. Полученный текст группируется в слова по смыслу.

Один из недостатков шифрования по таблице Вижинера - ненадежность шифрования при небольшой длине ключа и сложность формирования длинных ключей.

Т.к. в ключе не допускается повторение букв (в противном случае шифрование будет неоднозначным), а сам ключ должен легко запоминаться, последовательность букв, не имеющих определенного смысла, запомнить трудно.

С целью повышения надежности шифрования текста, предлагается усовершенствованный вариант таблицы Вижинера, который заключается в следующем:

1. Во всех строках, кроме первой, буквы алфавита располагаются в произвольном порядке.
2. Выбирается 10, не считая первой, строк, пронумерованных натуральными числами от 0 до 9.
3. В качестве ключа используются величины, выраженные бесконечным рядом чисел (например, число Пи).

Шифрование и расшифрование осуществляется в той же последовательности, что и в случае простой таблицы Вижинера.
Частным случаем метода замены, обеспечивающим надежное шифрование информации является использование алгебры матриц. Например, правило умножения матрицы на вектор. Это правило заключается в следующем:

 

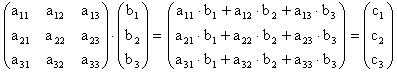
В соответствии с этим правилом, матрицу можно использовать в качестве основы для шифрования. Знаками вектора b₁ могут быть символы шифруемого текста, а знаками вектора результата c₁ - символы зашифрованного текста.

Для шифрования буквенных сообщений необходимо прежде всего заменить знаки алфавита их цифровым эквивалентом, которым может быть порядковый номер буквы в алфавите.

Для дешифрования используются те же самые правила умножения матрицы на вектор, только в качестве основы берется обратная матрица, а в качестве умножаемого вектора - соответствующее количество чисел шифрованного текста.

Цифрами вектора результата будут цифровые эквиваленты знаков исходного текста.

Существуют и другие методы подстановки.

Приведенные выше методы относятся к моноалфавитным подстановкам, которые можно представить как числовые преобразования букв исходного текста, рассматриваемых как числа.

Каждая буква в тексте умножается на некоторое число, называемое десятичным коэффициентом и прибавляется к некоторому другому числу (коэффициенту сдвига).

 

Получающееся число уменьшается по правилу вычитания модуля A, где A - размер алфавита и зашифрованный текст формируется из соответствующих ему алфавитных эквивалентов.

 

Аддитивные методы.

В качестве ключа в этих методах используется некоторая последовательность букв того же алфавита и такой же длины, что и в исходном тексте.

Шифрование выполняется путем сложения символов исходного текста и ключа по модулю, равному числу букв в алфавите.

Примером такого же метода является гаммирование, т.е. наложение на исходный текст некоторой последовательности кодов, называемой гаммой.

Процесс наложения осуществляется следующим образом:

1. Символы исходного текста и гамма представляются в двоичном коде и располагаются один под другим.
2. Каждая пара двоичных знаков заменяется одним двоичным знаком шифрованного текста в соответствии с принятым алгоритмом.
3. Полученная последовательность двоичных знаков шифрованного текста заменяется символами алфавита в соответствии с выбранным кодом.

Если ключ шифрования выбирается случайным образом, например, формируется с помощью датчика псевдослучайных чисел, то раскрыть информацию, не зная ключа практически невозможно.

Криптоанализ.

Криптоанализ - это наука получения открытого текста не имея ключа.
Успешно проведенный криптоанализ может раскрыть открытый текст или ключ.
Раскрытие ключа не криптологическим способом называют компрометацией.
Попытка криптоанализа называется вскрытием.
Существует 4 основных типа криптоаналитического вскрытия.
Для каждого из них предполагается, что криптоналитик обладает полнотой знаний об использовании алгоритма шифрования:

1. Вскрытие с использованием только шифротекста.
   У криптоаналитика есть шифротексты нескольких сообщений, зашифрованных одним и тем же алгоритмом шифрования. Задача криптоаналитика состоит в раскрытии открытого текста как можно большего числа сообщений или получения ключа, использованного для шифрования других сообщений, зашифрованных тем же ключом.
2. Вскрытие с использованием открытого текста.
   У криптоаналитика есть доступ не только к шифротекстам нескольких сообщений, но и к открытому тексту этих сообщений. Его задача состоит в получении ключа, использованного для шифрования сообщения, для дешифрования других сообщений, зашифрованных тем же ключом.
3. Вскрытие с использованием выбранного открытого текста.
   У криптоаналитика не только есть доступ к шифротекстам и открытым текстам нескольких сообщений, но и возможность выбирать открытый текст для шифрования.
4. Адаптивное вскрытие с использованием открытого текста.
   Это частный случай вскрытия с использованием выбранного открытого текста.
   Криптоаналитик не только может выбирать шифруемый текст, но также может строить свой последующий выбор на базе полученных результатов.
5. Вскрытие с использованием выбранного шифротекста.
   Криптоаналитик может выбрать различные шифротексты для шифрования и имеет доступ к дешифрованным открытым текстам.

Криптоаналитики часто используют индекс соответствия для определения того, находятся ли они на правильном пути.
Теоретически ожидаемое значение индекса соответствия определяется следующим выражением:

где N - длина сообщения в буквах,
m - число алфавитов.

Шифровки, которые дают значение индекса соответствия больше чем 0,066 - сами сообщают о том, что вероятно использовалась одноалфавитная подстановка. Если индекс соответствия находится между 0,052 и 0,066, то вероятно был использован двухалфавитный шифр подстановки.
0,047 < И.С. < 0,052 - трехалфавитный шифр.
Криптоаналитик берет наиболее часто встречающийся символ и предполагает, что это пробел, затем берет следующий наиболее частый символ и предполагает, что это буква "e" (для английских текстов) и т.д.
Принципиальное значение для надежности шифрования имеет длина кода ключа, т.е. отношение его длины к длине закрываемого им текста. Чем больше оно приближается к 1, тем надежнее шифрование.

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: