 |
Вычисляем среднее арифметическое
|
|
|
|
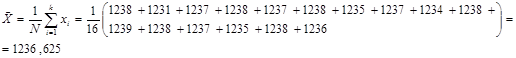
2) Вычисляем выборочную дисперсию:

3) Вычисляем среднее квадратичное отклонение:
S = 
4) Вычисляем коэффициент вариации:
С =  %
%
5) Записываем доверительный интервал:
[x - Дx; х + Дх], при этом заданная вероятность г = 0,95 заданный уровень значимости б = 1-г = 0,05
Дх - абсолютная ошибка;
Дх = 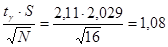
(число степеней свободы)=n - 1= 16-1=15; t0,95(15) = 2,13;
[1236,625 - 1,08; 1236,625+1,08]=[1235,544 1237,706].
6) Вычисляем относительную ошибку:

,09% ≤5% - результат хороший.
«Грубые» ошибки измерения исключаем с помощью правила 3-х у:
[x-3S; x+3S] = [1236,625-6,08; 1236,625+6,08]=[1230,538; 1242,712] - в данной выборке не присутствуют значения, которые бы не входили в интервал. Поэтому «грубых» ошибок нет.
Задание 2
Для исследования влияния некоторых факторов вакуумной сушки на усадку кожи по площади y (% полученной площади образца после сушки от первоначальной) были поставлены эксперименты по плану ПФЭ 23. В качестве факторов, влияющих на эту величину, были выбраны следующие:
z 1 - остаточное давление (кПа), z-1 =1,3, z+1 =91,3;
z 2 - сила механического прижатия полуфабриката кожи к греющей поверхности (кПа), z - 2 =0, z+2 =98;
z 3 - температура греющей поверхности (°С.), z - 3=30, z+3 =90.
Требуется построить уравнение регрессии, учитывая взаимодействия факторов, проверить полученную модель на адекватность и произвести ее интерпретацию. Исходные данные таблица 1.
искусственный кожа вакуумный сушка
Таблица 1 - Исходные данные
| Изучаемые факторы | Результаты опытов | |||||
| Z1 | Z2 | Z3 | Y1 | Y2 | Y3 | |
| 1 2 3 4 5 6 7 8 | - - - - + + + + | + + - - + + - - | + - + - + - + - | 93 95,7 78,5 88 95,4 84 97 90 | 94 95,9 79,3 88,1 95,6 85,4 97 90,7 | 95 95,9 79,5 88,3 95,5 85,3 97 91,1 |
Линейное уравнение регрессии относительно новых переменных при влиянии парных взаимодействий различных факторов на исследуемый параметр:
|
|
|
у = b0+b1x1+….+bkxk+b1,2x1x2+b1,3x1x3+….+bk-1,kxk-1xk, т.е.
y = b0+ 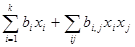
Рассчитываем среднее выборочное для каждого эксперимента:
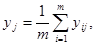 j = 1, n
j = 1, n
y1= 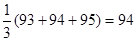 ;
;
 ;
;
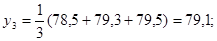
у4= …
и т.д.
Вычисляем коэффициенты уравнения регрессии:
b0=  ;
;
b1= 
b2= 
b3 =…
и т.д.
Найдем дисперсию воспроизводимости.

Определяем среднее квадратичное отклонение коэффициентов:
Sкоэф.= 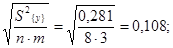
n (m-1)=8*2=16, б=0,05.
Находим критическое значение коэффициента:
tкр.=2,12
tкр*Sкоэф. =2,12*0.108=0.229.
Сравнивая полученные значения tкр*Sкоэф=0,229 с коэффициентами уравнения регрессии представленными в таблице 3, видим, что все коэффициенты кроме b4,7 больше по абсолютной величине 0,229. Следовательно, все коэффициенты кроме b4,7 значимы. Полагая, что b4,7 =0 получаем уравнение регрессии в кодированных переменных
у = 90,633+1,367х1+1,925х2+0,767х3+3,483х1х3+1,425х2х3.
Найдем значения изучаемого параметра по полученному уравнению регрессии
у1= 90,633-1,367+1,925+0,767-3,483+1,425=90,275;
у2= 90,633-1,367+1,925+0,767+3,483-1,425=92,108;
у3 = 90,633-1,367-1,925+0,767-3,483-1,425=82,825;
у4 = …
и т.д.
Вычисляем остаточную дисперсию:
S2ост. = 


Определяем расчетное значение критерия:
Fрасч.= 
Fтабл=4,494.
Так как Fрасч>Fтабл, то уравнение регрессии неадекватно.
Проводим интерпретацию полученной модели
у = 90,633+1,367х1+1,925х2+0,767х3+3,483х1х3+1,425х2х3.
Так как максимальный коэффициент стоит при х1х3 по абсолютной величине, то самое большое влияние оказывает первый и третий фактор, а именно температура нагрева электрода, скорость продвижения материала, при чем с увеличением этого фактора прочность сварки нетканого клеевого материала будет убывать. Далее по силе влияния на отклик (прочность сварки нетканого клеевого материала) идут: фактор х2 - давление роликов; парное взаимодействие х2х3 - давление роликов и скорость продвижение материала. С увеличением факторов х1х3,х1, х2, х2х3 увеличивается отклик, т.е. увеличивается прочность. С увеличением фактора х3 прочность будет убывать.
|
|
|
Выписываем уравнение регрессии в натуральных переменных. Для этого раскодируем переменные
х1=  ; х2 =
; х2 = 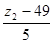 ; х3 =
; х3 = 
у = 90,633+1,367 ( )+1,925 (
)+1,925 ( )+0,763 (
)+0,763 ( )+3,483 (
)+3,483 (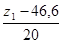 ) (
) ( )+1,425 (
)+1,425 (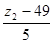 )(
)( ).
).
Заключение
В результате расчетов сводных статистических характеристик теплостойкости подошвенных композиций на основе термоэластопласта задание 1 не было выявлено грубых ошибок. По правилу «3у» все измерения входят в границы доверительного интервала. При проверки на ошибки по доверительной вероятности было выявлено, что необходимо отбросить 6 значений сверху и 5 значение снизу. Относительная ошибка равна 2,28%. Следовательно, результат измерения хороший.
При решении задания 2 было построено уравнение регрессии. Уравнение неадекватно, так как расчетное критерий Фишера больше табличного.
|
|
|


