 |
Глава 6. Способы измерения влияния факторов в детерминированном анализе
|
|
|
|
6.1. Способ цепной подстановки
Типы детерминированных моделей, в которых применяется способ цепной подстановки. Сущность и правила его применения. Алгоритмы расчета влияния факторов этим способом в различных типах моделей.
Одним из важнейших методологических вопросов в АХД является определение величины влияния отдельных факторов на прирост результативных показателей. В детерминированном факторном анализе (ДФА) для этого используются следующие способы: цепной подстановки, индексный, абсолютных разниц, относительных разниц, пропорционального деления, интегральный, логарифмирования и др.
Первые четыре способа основываются на методе элиминирования. Элиминировать — значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. Этот метод исходит из того, что все факторы изменяются независимо друг от друга: сначала изменяется один, а все другие остаются без изменения, потом изменяются два, затем три и т.д., при неизменности остальных. Это позволяет определить влияние каждого фактора на величину исследуемого показателя в отдельности.
Наиболее универсальным из них является способ цепной подстановки. Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей: аддитивных, мультипликативных, кратных и смешанных (комбинированных). Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и т.д. факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня определенного фактора позволяет элиминироваться от влияния всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя.
|
|
|
Порядок применения этого способа рассмотрим на следующем примере (табл. 6.1).
Т а б л и ц а 6.1
Данные для факторного анализа объема валовой продукции
| Показатель | Условное обозначение | План | Факт | +,- | Выполнение плана, % |
| Выпуск продукции, тыс. руб. | ВП | 160 000 | 240 000 | +80 000 | |
| Среднегодовая численность рабочих, чел. | ЧР | +200 | |||
| Отработано всеми рабочими за год: | |||||
| дней | D | 250 000 | 307 200 | +57 200 | 122,88 |
| часов | t | 2 000 000 | 2 334 720 | +334 720 | 116,736 |
| Среднегодовая выработка одного рабочего, тыс. руб. | ГВ | +40 | |||
| Количество отработанных дней одним рабочим за год | Д | +6 | 102,4 | ||
| Среднедневная выработка продукции одним рабочим, руб. | ДВ | -781,25 | + 141,25 | 122,1 | |
| Средняя продолжительность рабочего дня, ч. | П | 7.6 | -0.4 | ||
| Среднечасовая выработка, руб. | ЧВ | 102,796 | +22,796 | 128,5 |
Как нам уже известно, объем выпуска продукции (ВП)зависит от двух основных факторов первого уровня: численности рабочих (ЧР)и среднегодовой выработки (ГВ). Имеем двухфакторную мультипликативную модель: ВП = ЧР × ГВ.
Алгоритм расчета способом цепной подстановки для этой модели:
ВПпл = ЧРпл × ГВпл = 1000 × 160 = 160 000 тыс. руб.
ВПусл = ЧРф × ГВпл = 1200 × 160 = 192 000 тыс. руб.
ВПф = ЧРф × ГВф = 1200 × 200 = 240 000 тыс. руб.
Как видим, второй показатель валовой продукции отличается от первого тем, что при его расчете принята фактическая численность рабочих вместо запланированной. Среднегодовая выработка продукции одним рабочим в том и другом случае плановая. Значит, за счет увеличения количества рабочих выпуск продукции увеличился на 32 000 тыс. руб. ( 192 000– 160 000).
|
|
|
Третий показатель отличается от второго тем, что при расчете его величины выработка рабочих принята по фактическому уровню вместо плановой. Количество же работников в обоих случаях фактическое. Отсюда за счет повышения производительности труда объем выпуска продукции увеличился на 48 000тыс. руб. (240 000 – 192 000).
Таким образом, перевыполнение плана по выпуску продукции явилось результатом влияния следующих факторов:
а) увеличения численности рабочих + 32 000 тыс. руб.
б) повышения уровня производительности труда + 48 000 тыс. руб.
Итого + 80 000 тыс. руб.
Алгебраическая сумма влияния факторов обязательно должна быть равна общему приросту результативного показателя:
Δ ВПчр + Δ ВПгв = Δ ВПобщ.
Отсутствие такого равенства свидетельствует о допущенных ошибках в расчетах.
Для наглядности результаты анализа приведены в табл. 6.2.
Таблица 6.2
Результаты факторного анализа валовой продукции
| Показатель | Численность рабочих | Годовая вы работка, тыс. руб. | Выпуск продукции, млн. руб. | Отклонение от плана по выпуску продукции, млн. руб. | ||||||
| план | факт | план | усл. | факт | всего | в том числе засчет | ||||
| ЧР | ГВ | |||||||||
| Цех 1 | 39,6 | 46.2 | + 10.2 | + 3,6 | +6,6 | |||||
| Цех 2 | 55.5 | 60,0 | 66.0 | + 10,5 | +4,5 | +6,0 | ||||
| И т.д. | ||||||||||
| Всего | +80 | +32 | +48 |
Если требуется определить влияние трех факторов, то в этом случае рассчитывается не один, а два условных дополнительных показателя, т.е. количество условных показателей на единицу меньше числа факторов. Проиллюстрируем это на четырех-факторной модели валовой продукции:
ВП = ЧР × Д × П × ЧВ.
Исходные данные для решения задачи приведены в табл.6.1:
ВПпл = ЧРпл × Дпл × Ппл × ЧВпл = 1000 × 250 × 8 × 80 = 160 000 тыс. руб.
ВПусл 1 = ЧРф × Дпл × Ппл × ЧВпл = 1200 × 250 × 8 × 80 = 192 000 тыс. руб.
ВПусл 2 = ЧРф × Дф × Ппл × ЧВпл = 1200 × 256 × 8 × 80 = 196 608 тыс. руб.
ВПусл 3 = ЧРф × Дф × Пф × ЧВпл = 1200 × 256 × 7,6 × 80 = 186 778 тыс. руб.
ВПф = ЧРф × Дф × Пф × ЧВф = 1200 × 256 × 7,6 × 102,796 = 240 000 тыс. руб.
План по выпуску продукции в целом перевыполнен на 80 000 тыс. руб. (240 000 – 160), в том числе за счет изменения
|
|
|
а) количества рабочих
Δ ВПчр = ВПусл 1 - ВПпл = 192 000 -160 000 = +32 000;
б) количества отработанных дней одним рабочим за год
Δ ВПд = ВПусл 2 - ВПусл l = 196 608 - 192 000 = 4608;
в) средней продолжительности рабочего дня
Δ ВПп = ВПусл 3 - ВПусл 2 = 186 778 - 196 608 = -9830;
г) среднечасовой выработки
Δ ВПчв = ВПф - ВПусл 3 = 240 000 - 186 778 = +53 222
Всего + 80 000 тыс. руб.
При использовании способа цепной подстановки рекомендуется придерживаться определенной последовательности расчетов: в первую очередь нужно учитывать изменение количественных, а затем качественных показателей. Если же имеется несколько количественных и несколько качественных показателей, то сначала следует изменить величину факторов первого уровня подчинения, а потом более низкого. В приведенном примере объем производства продукции зависит от четырех факторов: количества рабочих, количества отработанных дней одним рабочим, продолжительности рабочего дня и среднечасовой выработки. Согласно схеме 5.2, количество рабочих в данном случае — фактор первого уровня подчинения, количество отработанных дней — второго уровня, продолжительность рабочего дня и среднечасовая выработка — факторы третьего уровня. Это и обусловило последовательность размещения факторов в модели и соответственно очередность их исследования.
Таким образом, применение способа цепной подстановки требует знания взаимосвязи факторов, их соподчиненности, умения правильно их классифицировать и систематизировать.
Мы рассмотрели пример расчета влияния факторов на прирост результативного показателя в мультипликативных моделях.
В кратных моделях алгоритм расчета факторов на величину исследуемых показателей следующий:
ФОпл =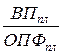 
; ФОусл = 
; ФОф = 
;
Δ ФОобщ = ФОф – ФОпл ,
в том числе
Δ ФОвп = ФОусл – ФОпл ,
Δ ФОопф = ФОф – ФОусл ,
где ФО — фондоотдача;
ВП — валовая продукция;
ОПФ — среднегодовая стоимость основных производственных фондов.
Методика расчета влияния факторов в смешанных моделях.
|
|
|
а) Мультипликативно-аддитивного типа П = VРП (Ц – С)
Ппл = VРПпл (Цпл – Спл); Δ Побщ = Пф – Ппл;
Пусл 1 = VРПф (Цпл – Спл); Δ Пvpn = Пусл 1 – Ппл;
Пусл 2 = VРПф (Цф – Спл); Δ Пц = Пусл 2 – П усл 1;
Пф = VРПф (Цф – Сф); Δ Пс = Пф – П усл 2;
где П — сумма прибыли от реализации продукции;
VРП — объем реализации продукции в натуральном измерении;
Ц — цена реализации;
С — себестоимость единицы продукции;
б) Кратно-аддитивного типа Y = 
Yпл = 
; Yусл 1 = 
Yусл 2 = 
; Yф = 
Δ Yобщ = Yф – Yпл; Δ Yа = Yусл 1 – Yпл;
Δ Yс = Yусл 2 – Yусл 1; Δ Yd = Yф – Yусл 2.
Аналогичным образом рассчитывают влияние факторов и по другим детерминированным моделям смешанного типа.
Отдельно необходимо остановиться на методике определения влияния структурного фактора на прирост результативного показателя с помощью этого способа. Например, выручка от реализации продукции (В)зависит не только от цены (Ц)и количества проданной продукции (VPП), но и от ее структуры (Удi). Если возрастет доля продукции высшей категории качества, которая продается по более высоким ценам, то выручка за счет этого увеличится, и наоборот. Факторная модель этого показателя может быть записана так:
В = 
.
В процессе анализа необходимо элиминироваться от воздействия всех факторов, кроме структуры продукции. Для этого сравниваем следующие показатели выручки:
Вусл 1= 
;
Вусл 2= 
;
Разность между этими показателями учитывает изменение выручки от реализации продукции за счет изменения ее структуры или сортового состава.
Из табл. 6.3 видно, что в связи с увеличением удельного веса продукции второго сорта в общем объеме его реализации выручка уменьшилась на 10 тыс. руб. (655 - 665). Это неиспользованный резерв предприятия.
Т а б л и ц а 6.3
Расчет влияния структурного фактора на изменение выручки от реализации продукции способом цепной подстановки
| Сорт продукции | Цена 1 т. руб. | Объем реализации, т | Структура продукции | Фактический VРП при плановой структуре, т | Выручка, тыс. руб. за УРПф при УДi | |||
| план | факт | план | факт | план | факт | |||
| 0.9 | 0,8 | 607,5 | ||||||
| 0,1 | 0.2 | 57,5 | ||||||
| Итого | - | 1.0 | 1,0 | 665,0 |
Индексный метод
Сущность и назначение индексного метода. Алгоритм расчета влияния факторов этим методом для разных моделей.
Индексный метод основан на относительных показателях динамики, пространственных сравнений, выполнения плана, выражающих отношение фактического уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде (или к плановому, или по другому объекту).
С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях.
|
|
|
Для примера возьмем индекс стоимости товарной продукции:
IТП = 
Он отражает изменение физического объема товарной продукции (q)и цен (р) и равен произведению этих индексов:
IТП = Iq × Ip.
Чтобы установить, как изменилась стоимость товарной продукции за счет количества произведенной продукции и за счет цен, нужно рассчитать индекс физического объема Iq и индекс цен Ip:
Iq = 
; Iр = 
В нашем примере объем выпуска продукции можно представить в виде произведения численности рабочих и их среднегодовой выработки. Следовательно, индекс валовой продукции Iв будет равен произведению индекса численности рабочих Iчр и индекса среднегодовой выработки Iгв:
Iвп = 
= 
= 
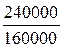= 1,5;
Iчр = 
= 
= 
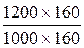= 1,2;
Iгв = 
= 
= 
= 1,25;
Iвп = Iчр × Iгв = 1,2 × 1,25 = 1,5.
Если из числителя вышеприведенных формул вычесть знаменатель, то получим абсолютные приросты продукции в целом и за счет каждого фактора в отдельности, т.е. те же результаты, что и способом цепной подстановки.
Способ абсолютных разниц
Сущность, назначение и сфера применения способа абсолютных разниц. Порядок и алгоритмы расчета влияния факторов этим способом
Способ абсолютных разниц является одной из модификаций элиминирования. Как и способ цепной подстановки, он применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных и мультипликативно-аддитивных моделях: Y = (a – b) c и Y = a (b – c). И хотя его использование ограничено, но благодаря своей простоте он получил широкое применение в АХД. Особенно эффективно применяется этот способ в том случае, если исходные данные уже содержат абсолютные отклонения по факторным показателям.
При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.
Рассмотрим алгоритм расчета для мультипликативной факторной модели типа Y = a × b × c × d. Имеются плановые и фактические значения по каждому факторному показателю, а также их абсолютные отклонения:
Δ а = аф – апл; Δ b = bф – bпл;
Δ с = сф – спл; Δ d = dф – dпл;
Определяем изменение величины результативного показателя за счет каждого фактора:
Δ Ya = Δ a × bпл × спл × dпл;
Δ Yb = aф × Δ b × спл × dпл;
Δ Yс = aф × bф × Δ с × dпл;
Δ Yd = aф × bф × сф × Δ d;
Как видно из приведенной схемы, расчет строится на последовательной замене плановых значений факторных показателей на их отклонения, а затем на фактический уровень этих показателей.
Рассмотрим методику расчета влияния факторов этим способом для четырехфакторной мультипликативной модели валовой продукции:
ВП=ЧР×Д×П× ЧВ: Δ ВПчр = (ЧРф –ЧРпл) Дпл ×Ппл×ЧВпл =
= (1200 - 1000) ×250 × 8,0 × 80,0 = +32 000 тыс. руб.;
Δ ВПд = ЧРф (Дф – Дпл) Ппл × ЧВпл =
= 1200 × (256 – 250) × 8,0 × 80,0 = +4608 тыс. руб.;
Δ ВПп = ЧРФ×ДФ [ ПФ-Ппл) × ЧВпл =
= 1200 × 256 × (7,6 – 8,0) × 80,0 = -9830 тыс. руб.;
ΔВП чв = ЧРф × Дф × Пф × (ЧВф – ЧВпл)=
= 1200 × 256 × 7,6 × (102,796 – 80) = +53 222 тыс. руб.
_______________________
Всего + 80 000 тыс. руб.
Таким образом, способ абсолютных разниц дает те же результаты, что и способ цепной подстановки. Здесь также необходимо следить за тем, чтобы алгебраическая сумма прироста результативного показателя за счет отдельных факторов была равна общему его приросту.
Рассмотрим алгоритм расчета факторов этим способом в смешанных моделях типа Y = (a – b) c. Для примера возьмем факторную модель прибыли от реализации продукции, которая уже использовалась в предыдущем параграфе:
П = VРП (Ц – С).
Прирост суммы прибыли за счет изменения объема реализации продукции:
Δ ПVРП = Δ VРП (Цпл – Спл).
цены реализации:
Δ Пц = VРПф × Δ Ц.
себестоимости продукции:
Δ Пс = VРПф × (–Δ С).
Расчет влияния структурного фактора при помощи этого способа проводится следующим образом:
Δ П = ∑ [(Удiф – Удiпл) × Цiпл ] × VРПобщ.ф.
Т а б л и ц а 6.4
Расчет влияния структурного фактора способом абсолютных разниц
| Сорт продукция | Цена 1т, руб. | Структура продукции | Изменение средней цены реализации за счет структуры продукции, руб. | ||
| план | факт | +,- | |||
| 0,9 | 0,8 | –0.1 | –270 | ||
| 0,1 | 0,2 | +0,1 | +230 | ||
| Всего | – | 1,0 | 1.0 | - | –40 |
Как видно из табл. 6.4, за счет изменения структуры реализации средняя цена за 1 т молока уменьшилась на 40 руб., а за весь фактический объем реализации продукции прибыли было получено меньше на 10 тыс. руб. (40 руб. х 250 т).
|
|
|
