 |
Контрольная работа (выполнить все три работы: 15 заданий)
|
|
|
|
Контрольная работа 1. (Темы 1 и 2.)
1. На производство поступила достаточно большая партия стержней длиной 250 и 190 см. Нужно получить 470 заготовок длиной 120 см. и 450 заготовок длиной 80. Отходы должны быть минимизированы. Построить математическую модель данной задачи.
Решение:
Это задача линейного программирования. Пусть, нужно использовать m длинных и n коротких стержней. Тогда m*250+n*190 
470*120+450*80, m 
0,n 0
От m1 стержней длиной 250 можно отрезать 2стержня по 120 и остаток 250-240=10
От m2 стержней длиной 250 можно отрезать 2стержня длиной 120 и 80 остаток 250-200=50
От m3 стержней длиной 250 можно отрезать 2стержня по 80 и остаток 250-160=90
От m4 стержней длиной 250 можно отрезать по 1стержню длиной 120 и остаток 250-120=130
От m5 стержней длиной 250 можно отрезать по 1стержню длиной 80 и остаток 250-80=170
От короткого n1 стержней длиной 190 можно отрезать по 1стержню длиной 120 и остаток 190-120=70
От n2 стержней длиной 190 можно отрезать по 2 стержня длиной 80 и остаток 190-80=110
От n3 стержней длиной 190 можно отрезать по 1 стержню длиной 80 и остаток 190-80=110
Тогда целевую функцию, которая равна общему объему отходов, можно записать так: Z =10 m1+50 m2 + 90m3+ 130 m4+ 170m5 + 70n1 + 30n2 + 110n3 -> min
Ограничения на ресурсы:
m1+m2+m3+m4+m5=m
n1+n2+n3=n,
m1,m2,m3,m4,m5,n1,n2,n3>=0
2. Найти максимум функции F = x1+x2 при условиях: 2x1+4x2 ≤ 16, -4x1+2x2 ≤ 8, x1+3x2 ≥ 9, x1,x2 ≥0. Обосновать.
Решение:
Необходимо найти максимальное значение целевой функции F = x1+x2 → max, при системе ограничений:
2x1+4x2≤16, (1)
-4x1+2x2≤8, (2)
x1+3x2≥9, (3)
x1 ≥ 0, (4)
x2 ≥ 0, (5)
Построим область допустимых решений, т.е. решим графически систему неравенств.
Построим уравнение 2x1+4x2≤16 по двум точкам. Пусть x1 = 0, тогда x2 = 4. Пусть x2 = 0, тогда x1 = 8. Соединяем точку (0;4) с (8;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости:2 • 0 + 4 • 0 - 16 ≤ 0, т.е. 2x1+4x2 - 16≤ 0 в полуплоскости ниже прямой.
Построим уравнение -4x1+2x2≤8 по двум точкам. Пусть x1 = 0, тогда x2 = 4. Пусть x2 = 0 тогда x1 = -2. Соединяем точку (0;4) с (-2;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости:-4 • 0 + 2 • 0 - 8 ≤ 0, т.е. -4x1+2x2 - 8≤ 0 в полуплоскости ниже прямой.
Построим уравнение x1+3x2≥9 по двум точкам. Пусть x1 = 0, тогда x2 = 3. Пусть x2 = 0, тогда x1 = 9. Соединяем точку (0;3) с (9;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости:1 • 0 + 3 • 0 - 9 ≤ 0, т.е. x1+3x2 - 9≥ 0 в полуплоскости выше прямой.
Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.
Построим прямую, отвечающую значению функции F = 0: F = x1+x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (1; 1). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.
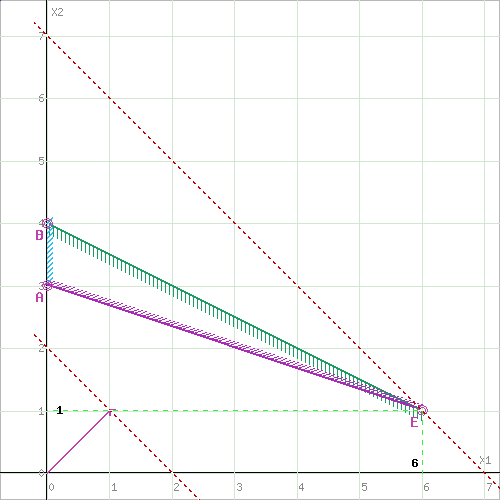
Прямая F(x) = const пересекает область в точке E. Так как точка E получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых:
2x1+4x2=16
x1+3x2=9
Решив систему уравнений, получим: x1 = 6, x2 = 1
Откуда найдем максимальное значение целевой функции:
Fmax(X) = 1*6 + 1*1 = 7
|
|
|
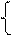Ответ: Fmax(X) = 7
3. Найти максимум функции F = 2x1+x2-x3+x4 -x5 при условиях x1+x2+x5=5, 2x1+x2+x4= 9, x1+2x2+x5=7, x1,x2,x3,x4 ,x5≥0. Указание: использовать симплекс метод.
Решение:
Определим максимальное значение целевой функции F(X) = 2x1+x2-x3+x4-x5 при следующих условиях-ограничений.
x1+x2+x5=5
2x1+x2+x4=9
x1+2x2+x5=7
Выразим целевую функцию через свободные переменные.
x4 = -2x1-x2
Получаем:
F(x) = 2x1+x2-x3+x4-x5=2x1+x2-x3+(-2x1-x2)-x5= - x3 - x5
Для построения первого опорного плана систему неравенств переходим к канонической форме.
Во 2-м равенстве базисной переменной является x4.
1x1 + 1x2 + 0x3 + 0x4 + 1x5 = 5
2x1 + 1x2 + 0x3 + 1x4 + 0x5 = 9
1x1 + 2x2 + 0x3 + 0x4 + 1x5 = 7
Введем искусственные переменные x: в 1-м равенстве вводим переменную x6; в 3-м равенстве вводим переменную x7;
1x1 + 1x2 + 0x3 + 0x4 + 1x5 + 1x6 + 0x7 = 5
2x1 + 1x2 + 0x3 + 1x4 + 0x5 + 0x6 + 0x7 = 9
1x1 + 2x2 + 0x3 + 0x4 + 1x5 + 0x6 + 1x7 = 7
Для постановки задачи на максимум целевую функцию запишем так:
F(X) = - Mx1 - Mx2-1x3 - Mx4-1x5 - Mx6 - Mx7 → max
За использование искусственных переменных, вводимых в целевую функцию, накладывается так называемый штраф величиной М, очень большое положительное число, которое обычно не задается.
Полученный базис называется искусственным, а метод решения называется методом искусственного базиса.
Из уравнений выражаем искусственные переменные:
x6 = 5-x1-x2-x5
x7 = 7-x1-2x2-x5
которые подставим в целевую функцию:
F(X) = -x3-x5 - M(5-x1-x2-x5) - M(7-x1-2x2-x5) → max
или
F(X) = (2M)x1+(3M)x2+(-1)x3+(-1+2M)x5+(-12M) → max
Решим систему уравнений относительно базисных переменных: x6, x4, x7
Полагая, что свободные переменные равны 0, получим первый опорный план:
X0 = (0,0,0,9,0,5,7)
Базисное решение называется допустимым, если оно неотрицательно.
|
|
|
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 | min |
| x6 | |||||||||
| x4 | |||||||||
| x7 | 31/2 | ||||||||
| F(X0) | -12M | -2M | -3M | 1-2M |
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю.
min (5: 1, 9: 1, 7: 2) = 31/2. 3-ая строка является ведущей.
Разрешающий элемент равен 2 и находится на пересечении ведущего столбца и ведущей строки.
Пересчитаем симплекс-таблицу.
| B | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| 5-(7 • 1):2 | 1-(1 • 1):2 | 1-(2 • 1):2 | 0-(0 • 1):2 | 0-(0 • 1):2 | 1-(1 • 1):2 | 1-(0 • 1):2 | 0-(1 • 1):2 |
| 9-(7 • 1):2 | 2-(1 • 1):2 | 1-(2 • 1):2 | 0-(0 • 1):2 | 1-(0 • 1):2 | 0-(1 • 1):2 | 0-(0 • 1):2 | 0-(1 • 1):2 |
| 7: 2 | 1: 2 | 2: 2 | 0: 2 | 0: 2 | 1: 2 | 0: 2 | 1: 2 |
| (0)-(7 • (-3M)):2 | (-2M)-(1 • (-3M)):2 | (-3M)-(2 • (-3M)):2 | (1)-(0 • (-3M)):2 | (0)-(0 • (-3M)):2 | (1-2M)-(1 • (-3M)):2 | (0)-(0 • (-3M)):2 | (0)-(1 • (-3M)):2 |
Получаем новую симплекс-таблицу:
|
|
|
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 | min | |
| x6 | 11/2 | 1/2 | 1/2 | -1/2 | ||||||
| x4 | 51/2 | 11/2 | -1/2 | -1/2 | 32/3 | |||||
| x2 | 31/2 | 1/2 | 1/2 | 1/2 | ||||||
| F(X1) | -11/2M | -M | 1-M | 11/2M |
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x1.
min (11/2: 1/2, 51/2: 11/2, 31/2: 1/2) = 3, 1-ая строка является ведущей.
Разрешающий элемент равен (1/2).
Пересчитаем симплекс-таблицу.
| B | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| 11/2: 1/2 | 1/2: 1/2 | 0: 1/2 | 0: 1/2 | 0: 1/2 | 1/2: 1/2 | 1: 1/2 | -1/2: 1/2 |
| 51/2-(11/2 • 11/2):1/2 | 11/2-(1/2 • 11/2):1/2 | 0-(0 • 11/2):1/2 | 0-(0 • 11/2):1/2 | 1-(0 • 11/2):1/2 | -1/2-(1/2 • 11/2):1/2 | 0-(1 • 11/2):1/2 | -1/2-(-1/2 • 11/2):1/2 |
| 31/2-(11/2 •1/2):1/2 | 1/2-(1/2 •1/2):1/2 | 1-(0 •1/2):1/2 | 0-(0 •1/2):1/2 | 0-(0 •1/2):1/2 | 1/2-(1/2 •1/2):1/2 | 0-(1 •1/2):1/2 | 1/2-(-1/2 •1/2):1/2 |
| (11/2M)-(11/2 • (-M)):1/2 | (-M)-(1/2 • (-M)):1/2 | (0)-(0 • (-M)):1/2 | (1)-(0 • (-M)):1/2 | (0)-(0 • (-M)):1/2 | (1-M)-(1/2 • (-M)):1/2 | (0)-(1 • (-M)):1/2 | (11/2M)-(-1/2 • (-M)):1/2 |
Получаем новую симплекс-таблицу:
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x1 | -1 | |||||||
| x4 | -2 | -3 | ||||||
| x2 | -1 | |||||||
| F(X2) | M | M |
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Так как в оптимальном решении отсутствуют искусственные переменные (они равны нулю), то данное решение является допустимым.
Оптимальный план можно записать так:
x1 = 3, x2 = 2, x3 = 0, x4 = 1, x5 = 0
Fmax(X) = 2•3 + 1•2 -1•0 + 1•1 -1•0 = 9
Ответ: Fmax(X) = 9
4.Для производства продукции трёх видов A, B, C используются три различных вида сырья. Каждый из видов сырья может быть использован в объёме не большем, чем 180, 210 и 236 кг. соответственно. Нормы затрат каждого из видов сырья на 1 кг. продукции данного вида и цена единицы продукции каждого вида приведены в таблице:
| Вид сырья | Нормы затрат сырья на единицу продукции | ||
| Изделие A | Изделие B | Изделие C | |
| I | |||
| II | |||
| III | |||
| Цена 1 кг. продукции (т.р.) |
Потратив 50 т.р. фирма может открыть производство 4-го вида продукции, нормы затрат сырья на единицу которого составляют 2, 4 и 3 кг. соответственно, а цена 1 кг. равна 18 т.р. При этом функциональность старых линий производства не нарушается. Определить, окупится ли открытие новой линии производства при таких предположениях.
|
|
|
Решение:
Введем следующие обозначения и получим:
Х1 – планируемый объем выпуска изделий A вида;
Х2 –планируемый объем выпуска изделий B вида;
Х3 -планируемый объем выпуска изделий C вида.
Составляем экономико-математическую модель задачи, которая включает целевую функцию и систему линейных ограничений. Составим целевую функцию, выражающую общий объем выручки при продаже выпускаемых изделий:
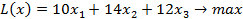
Составим ограничения на имеющиеся ресурсы:
Решим задачу симплекс методом
Для построения первого опорного плана переходим к канонической форме..
4x1 + 2x2 + 1x3 + 1x4 + 0x5 + 0x6 = 180
1x1 + 2x2 + 5x3 + 0x4 + 1x5 + 0x6 = 236
3x1 + 1x2 + 3x3 + 0x4 + 0x5 + 1x6 = 210
Решим систему уравнений относительно базисных переменных: x4, x5, x6
Полагая, что свободные переменные равны 0, получим первый опорный план:
X0 = (0,0,0,180,236,210)
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | min | |
| x4 | |||||||||
| x5 | |||||||||
| x6 | |||||||||
| F(X0) | -10 | -14 | -12 |
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю.
min (180: 2, 236: 2, 210: 1) = 90
Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (2).
Пересчитаем симплекс-таблицы.
| B | x1 | x2 | x3 | x4 | x5 | x6 |
| 180: 2 | 4: 2 | 2: 2 | 1: 2 | 1: 2 | 0: 2 | 0: 2 |
| 236-(180 • 2):2 | 1-(4 • 2):2 | 2-(2 • 2):2 | 5-(1 • 2):2 | 0-(1 • 2):2 | 1-(0 • 2):2 | 0-(0 • 2):2 |
| 210-(180 • 1):2 | 3-(4 • 1):2 | 1-(2 • 1):2 | 3-(1 • 1):2 | 0-(1 • 1):2 | 0-(0 • 1):2 | 1-(0 • 1):2 |
| 0-(180 • -14):2 | -10-(4 • -14):2 | -14-(2 • -14):2 | -12-(1 • -14):2 | 0-(1 • -14):2 | 0-(0 • -14):2 | 0-(0 • -14):2 |
Получаем новую симплекс-таблицу:
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | min |
| x2 | 1/2 | 1/2 | ||||||
| x5 | -3 | -1 | ||||||
| x6 | 21/2 | -1/2 | ||||||
| F(X2) | -5 |
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.В качестве ведущего выберем столбец, соответствующий переменной x3.
min (90: 1/2, 56: 4, 120: 21/2) = 14. Следовательно, 2-ая строка является ведущей.
Разрешающий элемент равен (4).
Пересчитаем симплекс-таблицу.
| B | x1 | x2 | x3 | x4 | x5 | x6 |
| 90-(56 • 1/2):4 | 2-(-3 • 1/2):4 | 1-(0 • 1/2):4 | 1/2-(4 • 1/2):4 | 1/2-(-1 • 1/2):4 | 0-(1 • 1/2):4 | 0-(0 • 1/2):4 |
| 56: 4 | -3: 4 | 0: 4 | 4: 4 | -1: 4 | 1: 4 | 0: 4 |
| 120-(56 • 21/2):4 | 1-(-3 • 21/2):4 | 0-(0 • 21/2):4 | 21/2-(4 • 21/2):4 | -1/2-(-1 • 21/2):4 | 0-(1 • 21/2):4 | 1-(0 • 21/2):4 |
| 1260-(56 • -5):4 | 18-(-3 • -5):4 | 0-(0 • -5):4 | -5-(4 • -5):4 | 7-(-1 • -5):4 | 0-(1 • -5):4 | 0-(0 • -5):4 |
Получаем новую симплекс-таблицу:
|
|
|
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| x2 | 23/8 | 5/8 | -1/8 | ||||
| x3 | -3/4 | -1/4 | 1/4 | ||||
| x6 | 27/8 | 1/8 | -5/8 | ||||
| F(X2) | 141/4 | 53/4 | 11/4 |
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Оптимальный план можно записать так:
x1 = 0, x2 = 83, x3 = 14
F(X) = 10•0 + 14•83 + 12•14 = 1330
В оптимальный план вошла дополнительная переменная x6. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 3-го вида в количестве 85.
Значение 141/4> 0 в столбце x1 означает, что использование x1 - не выгодно.
Значение 0 в столбце x2 означает, что использование x2 - выгодно.
Значение 0 в столбце x3 означает, что использование x3 - выгодно.
Значение 53/4 в столбце x4 означает, что теневая цена (двойственная оценка) равна y1=53/4.
Значение 11/4 в столбце x5 означает, что теневая цена (двойственная оценка) равна y2=11/4.
Оптимальный план двойственной задачи равен:
y1 = 53/4, y2 = 11/4, y3 = 0
Z(Y) = 180*53/4+236*11/4+210*0 = 1330
Если в план включаются новые виды продукции, то оценка целесообразности их введения определяется по формуле
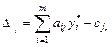
где аij - объем ресурсов i-го типа, которые требуются на производство единицы продукции j-го вида, cj - прибыль от реализации единицы продукции j - го вида. Оценим целесообразность включения в план нового вида продукции ценой 18 единиц, если нормы затрат ресурсов 2, 4, 3 единиц:
2*53/4 + 4*11/4 + 3*0 -18 ≤ 1,5
прибыль превышает затраты и введение в план производства пятого вида изделия целесообразно.
|
|
|
