 |
Задача №5. Кручение валов кругового сечения
|
|
|
|
ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Императора Александра I
Кафедра «Прочность материалов и конструкций»
Прикладная механика 2
Вариант № 8
Выполнил:Богатова Н.А.
Уч.шифр:13-УППц-308
Проверил:
Г.Санкт-Петербург
2015 год
Задача №1. Расчет прямоосного ступенчатого стержня
На осевое действие сил
Исходные данные:
a =0.7 м, b =0.8 м, c =0.7 м, F1 =40 кН, F2 =120 кН, F3 =60 кН, q =100 кН / м, [ σ ]=12 МПа, Е =104 ГПа.
Рис.1.1 Схема стержня и эпюра продольных сил Nz
Запишем уравнение равновесия всех сил на ось z и найдем реакцию опоры:
В пределах каждого участка проводится сечение и показывается отсеченная часть (рис.2 а,б,в). Для каждой отсеченной части записываем уравнение равновесия и строим эпюры:
Рис. 1.2 Отсеченные части стержня
На рисунке 1.1 показана эпюра продольных сил для ступенчатого стержня. Найдем площадь для каждого участка из условия прочности, используя следующую формулу:
,
где Ai – площадь поперечного сечения i-го участка,
| Ni |max – максимальное значения усилия на i-го участка,
[ σ ] – допускаемое значение нормального напряжения материала стержня.
Используя эпюру продольных сил, получим следующие значения площадей:
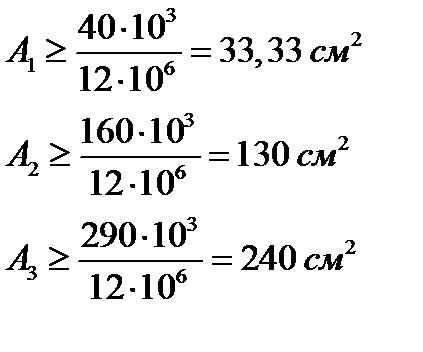
Найдем перемещение точки К по формуле:
где ωNi – площадь (с учетом знака) эпюры продольной силы і-го участка,
EAi – продольная жесткость i-го участка стержня.
Подставим значения и получим:
Задача №2. Расчет статически определимой
Шарнирно-стержневой системы
Исходные данные:
а = 1.6 м, b = 1.6 м, h = 1.2 м, α = 50, F = 60 кН, q = 50 кН/м, для дерева: Eд = 104 МПа, [ σ ] = 12 МПа; для стали: Eст = 2`105 МПа, [ σ ] = 160 МПа.
Рис.2.1 Схема шарнирно-стержневой системы
|
|
|
Для определения реакций опор и усилий в элементах шарнирно-стержневых систем рассматривается равновесие абсолютно жесткого диска (элемент с штриховкой). Для этого заменим стержни на реакции и получим расчетную схему, представленную на рис. 2.
Рис. 2 Расчетная схема
Для заданной расчетной схемы запишем уравнения равновесия и найдем усилия в стержнях.
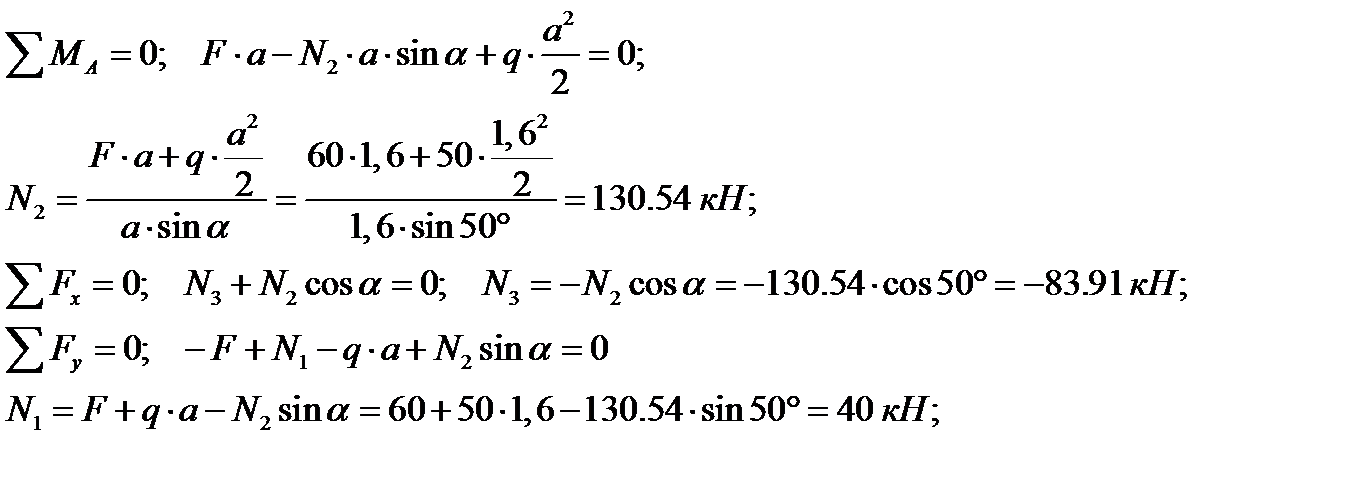
Найдем площади на каждом стержне из условия прочности. Для стержней 1 и 2 площадь будет равна:
Тогда размеры поперечного сечения квадрата будут равны a2 =0.105 м.
Найдем площадь для третьего стержня, круглого поперечного сечения:
Тогда размеры диаметра круга будут равны d = 0.074 м.
Найдем удлинения каждого стержня по формуле:
,
где Ni – усилие действующее в i-м стержне,
li – длина i-го стержня,
EAi – продольная жесткость i-го стержня.
Подставим значения получим:
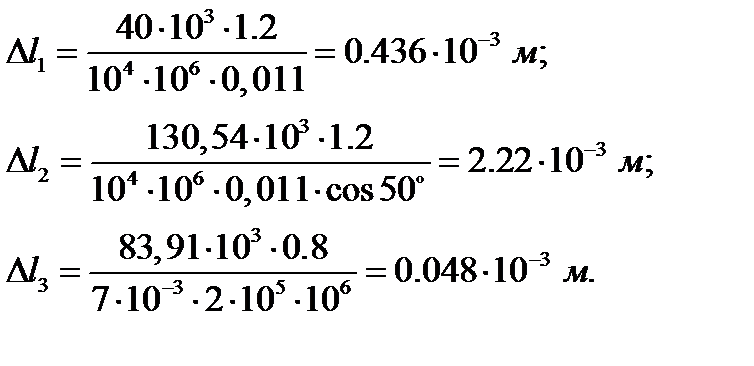
Задача №5. Кручение валов кругового сечения
Исходные данные:
a = 1.4 м, b = 1.4 м, c = 1.8 м, М1 = 70 кН·м, М2 = 60 кН·м, М3 = 60 кН·м, [ φ ] = 0.4 град/м, [ τ ] = 80 МПа, G = 0.8·105 МПа.
Рис. 1 Схема вала
Запишем уравнение равновесия относительно оси вала и найдем неизвестный момент M0:
Построим эпюру моментов показанную на рис.1. Для этого разобьем вал на три участка по методу сечений и рассмотрим их равновесие.
1 участок:
0≤z≤a
2 участок:
a≤z≤a+b
3 участок:
a+b≤z≤a+b+c
Рис.2 Разбиение на участки
Из условий прочности и жесткости подберем сечения вала в виде круга.
Условие прочности: 
, где 
, полярный момент сопротивления. Тогда диаметр круга равен:
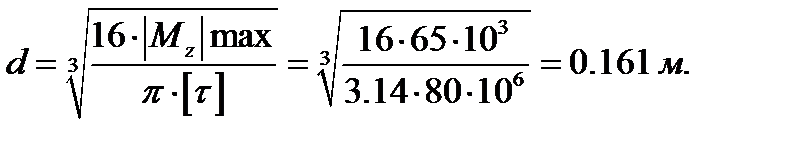
Условие жесткости: 
, где 
, полярный момент инерции. Тогда диаметр круга равен:
Выбираем наибольший диаметр d = 0.186 м.
Аналогично подберем поперечное сечение для полого вала, принимая отношение 
Тогда из условий прочности и жесткости получим:
Выбираем наибольший диаметр D = 0.212 м.
Вычислим в процентах величину экономии материла для полого вала:
|
|
|
Полый вал экономично эффективен по сравнению с кругом на 55.6%.
Построим эпюру углов закручивания используя формулу 
. Поскольку вал в виде колец более эффективен, то строим для полого вала, принимая в качестве неподвижного левое крайнее сечение.
Тогда получим:
1 участок 0≤z≤a
2 участок a≤z≤a+b
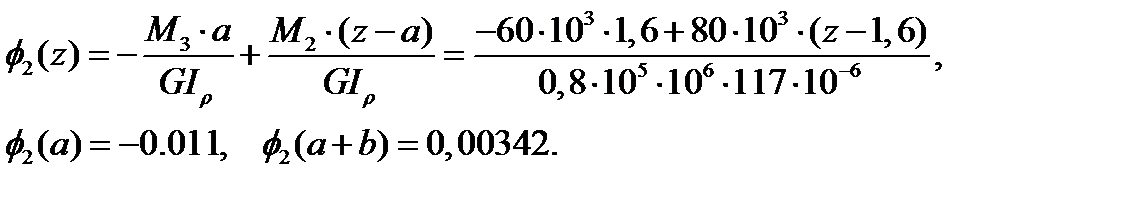
3 участок a+b≤z≤a+b+c
Эпюра углов закручивания представлена на рис.1.
|
|
|
