 |
Аналог уравнений Коши-Римана.
|
|
|
|
Дуальные числа.
Определение дуальных чисел.
Алгебра дуальных чисел образуется удвоением по Кэли алгебры действительных чисел:
Q = D1 + E * D2
С мнимой единицей удвоения E2=0. Дуальное число есть пара действительных чисел, которые называют его компонентами. Обычно дуальную мнимую единицу обозначают буквой w. Тогда дуальное число может быть представлено:
В такой записи дуального числа q его компоненты q0 и q1 называются действительной (или главной) и дуальной (или мнимой) частями соответственно. Таблица произведений единиц базиса дуальных чисел имеет вид:
| 1 | w | |
| 1 | 1 | w |
| w | w | 0 |
Дуальные числа q и p считаются равными, если равны их компоненты:

Дуальное число p равно нулю в случае, если p0=0 и p1=0.
Как и для других гиперкомплексных чисел, операции сложения и вычитания для дуальных чисел определяются покомпонентно:
Мнимую часть дуального числа также иногда называют моментной частью, а отношение мнимой части к действительной называют параметром:
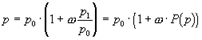
, или
если

2. Свойства дуальных чисел.
В силу определения мнимой единицы w² = 0 для умножения дуальных чисел получаем формулу:

Для деления p/q при q0 ¹ 0 получим:

Для возведения дуального числа в степень справедлива формула:

Для извлечения корня степени n из дуального числа p справедлива формула:

В случае же p0 = 0 операция извлечения корня не определена.
Для параметра дуального числа справедливы два интересных соотношения:
Параметр произведения дуальных чисел равен сумме параметров сомножителей:

Параметр частного двух дуальных чисел равен разности параметров делимого и делителя:

Так как для числа p где параметр равен бесконечности и, поскольку действительная часть произведения равна произведению действительных частей, действительную часть дуального числа принято называть модулем дуального числа:
|
|
|

При таком выборе определения модуля для дуального числа сохраняется его основное свойство мультипликативности:

Функция и дифференциал функции.
Будем следовать классическому определению функции как закону отображения области определения в область значений. В случае, если областью определения и областью значений является область дуальных чисел, функцию можно представить покомпонентно:

где f1 и f2 - две вещественные функции двух аргументов.
К основному соотношению в функциональном анализе гиперкомплексных чисел относят аналог уравнений Эйлера. Мы также присоединяюсь к этому мнению в силу чрезвычайной важности этого соотношения:
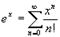
и для случая дуальных чисел имеем:
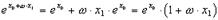
В частности,

Для элементарных функций дуального аргумента справедливы соотношения:










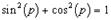
Для дифференциала функции дуального аргумента также используем класическое определение дифференциала как разность значений функции до и после приращения аргумента:
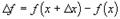
Аналог уравнений Коши-Римана.
В теории функций комплексного переменного особую важность имеют аналитические функции, для которых предел отношения приращения функции к приращению аргумента не зависит от отношения мнимой и действительной частей приращения аргумента. Что на комплексной плоскости иллюстрируется независимостью производной от направления приращения аргумента. Обозначив производную функции f как f’, получим:

В теории конформных отображений сей факт может быть трактован геометрически - угол между направлением приращения функции и направлением приращения аргумента зависит только от точки, в которой взята производная.
Рассмотрим аналогичное требование для случая дуального переменного и посмотрим, что из этого получится:
|
|
|


Чтобы удовлетворить поставленному ограничению, следует положить равными нулю множители перед dx1/dx0. Тогда получим:


Эти соотношения и есть аналог уравнений Коши-Римана для функций дуального переменного. Из первого из этих соотношений вытекает, что функция f0 есть функция только переменной x0:
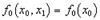
А из второго - выражение для f1
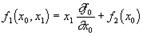
Где (x0)- некоторая функция только одного переменного x0.
Таким образом, общее выражение функции дуального переменного

удовлетворяющее независимости производной от направления приращения аргумента, будет иметь вид:
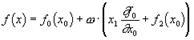
В случае вещественного x (x1=0) функция будет иметь вид:

Положим, что в общем случае функция дуального переменного зависит также от дуальных параметров A, B, C,... и определим её с помощью ряда Тейлора, в котором w * x1играет роль приращения и положим равными нулю все члены, содержащие w в степени выше первой.


Сравнив с выражением для функции одного переменного, получим:

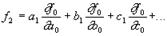
Действительная часть функции равна функции от действительных частей величин, от которых она зависит. Также из приведенных соотношений можно сделать важный вывод, а именно: функция дуальной переменной x = x0 +w * x1 полностью определяется функцией от главной части переменной, x0. Отсюда также следует, что если главные части двух функций тождественно равны, то равны и сами эти функции.
Используя соотношения Коши-Римана для функций дуального переменного, можем получить выражение для производной функции f(x):

Таким образом, дифференцирование по дуальной переменной x сводится к дифференцированию по вещественной переменной x0.
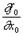 |
Если некоторая функция j(x), являющаяся главной частью F(x), тождественно равна
, то отсюда будет следовать, что функция F(x) будет равна df/dx. Дифференцируя равенство
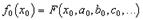
и
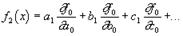
по x, на основании равенства
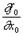 |
j =
, получим:

Откуда получим:
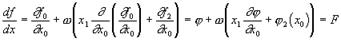
Если F - функция дуальной переменной x и дуальных параметров A, B, C,..., то функцию G от тех же величин, тождественно удовлетворяющую уравнению

назовем интегралом от Fdx и обозначим так:

Отсюда следует, что

Таким образом, в области дуальных чисел сохраняются все теоремы дифференциального и интегрального исчислений. Приведем основные соотношения для элементарных функций:
|
|
|
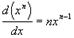



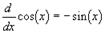 |
|
|
|


