 |
Распределение молекул по скоростям.
|
|
|
|
Равновесное состояние системы – это состояние, при котором макропараметры системы не изменяются, такие, как давление и температура. Однако скорости молекул различны.
Уточним распределение молекул по скоростям.
Самое важное – это определить, что мы должны найти. Не имеет смысла ставить вопрос о значении скоростей отдельных молекул, так как мы знаем, что молекула испытывает непрерывные соударения, и скорость ее меняется. Также неправильно пытаться найти число молекул, обладающих данной скоростью, так как это число также меняется.
В данный момент времени скоростью 100 м/с обладают 10000 молекул, а в следующий момент времени – 10 001, в следующий – 9 998 и т. д.
Поэтому имеет смысл так поставить вопрос: надо определить число молекул dN, имеющих скорость, находящуюся в интервале от 
.
Отметим что, хотя происходят непрерывные столкновения молекул, при которых их скорость меняет направление и значение, количество молекул, скорости которых находятся в интервале от остается неизменным.
Очевидно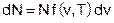 
, где 
функция распределения молекул по скоростям.
Выражение для этой функции, найденное Максвеллом и подтвержденное экспериментально, имеет вид (рис. 1):
.
N – число молекул, m – масса молекулы, Т – температура, k – постоянная Больцмана.
Рис. 1
Относительное число молекул, скорости которых находятся в интервале dv, можно найти, умножив функцию распределения на интервал: 
.
При более высоких температурах кривая смещается в сторону больших скоростей, однако площадь под кривой остается неизменной и равной единице.
Как мы видим из рисунка, кривая имеет максимум, vн – наивероятнейшая скорость, которую можно найти, исследовав функцию распределения на экстремум.
|
|
|
.
Средняя арифметическая скорость равна
, где 
число молекул, обладающих скоростью vi.
Переходя к пределу, найдем среднюю арифметическую скорость через функцию распределения:
Средний квадрат скорости определяется по формуле:
Итак,
Ряд опытов для определения скорости молекул был сделан Штерном (1888 – 1969).
Рассмотрим схему одного из опытов.
Прибор Штерна состоит из двух коаксиальных цилиндров, жестко связанных друг с другом, вдоль оси цилиндров натянута тонкая платиновая проволока, покрытая слоем серебра. Воздух из прибора откачан. Цилиндры могут вращаться. В малом цилиндре делается узкая щель.
По проволоке пропускают электрический ток, проволока нагревается, и атомы серебра испаряются, проходя через щель, они осаждаются на внутренней поверхности большого цилиндра, образуя полоску.
Затем цилиндры приводятся во вращение, и полоска смещается (см.рис.).
Средняя скорость молекул рассчитывается по формуле:
Флуктуации.
Число молекул, находящихся в любом объеме газа, не остается постоянным. Число молекул колеблется около среднего значения. Случайные отклонения числа молекул, плотности, температуры называются флуктуациями. Роль флуктуаций в различных физических явлениях чрезвычайно велика. За количественную меру флуктуации принимается относительная флуктуация 
.
– среднее значение.
При больших значениях N, как установил Смолуховский,
.
Примеры решения задач.
Задача 1. При каком количестве молекул газа, и в каком объеме относительная флуктуация равна 1 %?
Решение
Воспользуемся формулой Смолуховского.
0,01 = 
.
Это количество молекул при нормальных условиях занимает объем, равный
. Тогда 
В больших объемах флуктуации будут значительно меньше.
Задача 2. По газопроводу течет углекислый газ при давлении р = 50 Па и температуре t° = 17°C. Какова скорость движения газа по трубе, если за t = 5 мин через площадь поперечного сечения S = 6 см2 протекает m = 2,5 кг углекислого газа?
|
|
|
Решение
Для ответа на вопрос задачи необходимо определить объем газа, протекающего через поперечное сечение трубы. По условию задачи даны давление, температура и масса, а также известно, какой движется по трубе газ. Согласно уравнению Менделеева-Клапейрона запишем
, (1)
М – молярная масса углекислого газа СО2, равная М = 0,044 кг/моль.
Из (1) найдем
.
Этот объем газа проходит через сечение S за время t, следовательно,
V = vSt,
откуда
Проверим размерность.
.
|
|
|
