Главная | Обратная связь | Поможем написать вашу работу!

И идентификация объектов управления

МОДЕЛИРОВАНИЕ

И ИДЕНТИФИКАЦИЯ ОБЪЕКТОВ УПРАВЛЕНИЯ

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

для бакалавров специальности 5В070200 «Автоматизация и управление»

Шымкент, 2016 г.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН

южно-казахстанский государственный университет

им. м.ауезова

Кафедра Автоматизации, телекоммуникаций и управления

Тасанбаев С. Е.

МОДЕЛИРОВАНИЕ

И ИДЕНТИФИКАЦИЯ ОБЪЕКТОВ УПРАВЛЕНИЯ

Лабораторный практикум

для бакалавров специальности 5В070200 «Автоматизация и управление»

Шымкент, 2016 г

УДК 519.87

ББК 22.18

Составитель к.т.н., доцент Тасанбаев С. Е.. Лабораторный практикум по дисциплине «Моделирование и идентификация объектов управления» -, Шымкент: ЮКГУ им. М. Ауезова, 2016, -65 с.

Лабораторный практикум составлен в соответствии с требованиями учебного плана и программой дисциплины «Моделирование и идентификация объектов управления» и включает все необходимые сведения по выполнению лабораторных занятий курса.

Лабораторный практикум предназначен для студентов 5В070200 «Автоматизация и управление»

Лабораторный практикум содержит цели, краткие теоретические сведения, описание используемого программного обестечения, порядок выполнения работы, обработка полученных результатов и контрольные вопросы десяти лабораторных работ.

Рецензенты:

д.т.н., профессор кафедры ВПО ЮКГУ Бреннер А. М.

к.т.н., доцент, руководитель филиала №89 НТЦ МОНРК Каланов C.M.

Рассмотрено и рекомендовано к печати заседанием кафедры «Автоматизация, телекоммуникации и управление» (протокол № 5 от «12» декабря 2016 г.) и комитетом по инновационным технологиям обучения и методическому обеспечению высшей школы Информационные технологии и энергетика» протокол № от «» 201 г.

Рекомендовано к изданию Методическим советом ЮКГУ им. М.Ауезова,

протокол № от «» 201 г.

Содержание

Стр

Введение. 5

Лабораторная работа №1 «Идентификация параметров статической модели объекта» 8

1.1 Цели и задачи работы.. 8

1.2 Содержание работы.. 8

1.3 Оборудование, технические и инструментальные средства. 13

1.4 Порядок выполнения работы.. 13

1.5 Контрольные вопросы.. 13

1.6 Контрольный пример. 14

Лабораторная работа №2 «Однофакторный дисперсионный анализ объекта». 16

2.1 Цели и задачи работы.. 16

2.2 Содержание работы.. 16

2.3 Оборудование, технические и инструментальные средства. 17

2.4 Порядок выполнения работы.. 18

2.5 Контрольные вопросы: 18

2.6 Контрольный пример. 18

Лабораторная работа №3 «Статистическая оценка параметров распределения случайных величин. Проверка гипотез». 20

3.1 Цели и задачи работы.. 20

3.2 Содержание работы.. 20

3.3 Оборудование, технические и инструментальные средства. 23

3.4 Порядок выполнения работы.. 23

3.5 Контрольные вопросы.. 23

3.6 Контрольный пример. 24

Лабораторная работа №4 «Определение параметров модели методами планирования эксперимента». 26

4.1 Цели и задачи работы.. 26

4.2 Содержание работы.. 28

4.3 Оборудование, технические и инструментальные средства. 29

4.4 Контрольные вопросы: 29

4.5 Контрольный пример. 29

4.6 Контрольный пример. 31

Лабораторная работа №5 «Идентификация динамических характеристик объектов» 34

5.1 Цели и задачи работы.. 34

5.2 Идентификация динамических характеристик объектов с самовыравниванием 35

5.3 Оборудование, технические и инструментальные средства. 39

5.4 Порядок выполнения работы.. 39

5.5 Идентификация динамических характеристик объектов без самовыравнивания. 40

5.6 Проверка адекватности. 41

5.7 Методика проведения эксперимента. 45

Лабораторная работа №6 «Оптимальная линейная фильтрация по Калману». 49

6.1 Постановка задачи. 49

Лабораторная работа №7» Определение параметров регрессионной модели с использованием рекуррентных методов оценивания. Непараметрические методы идентификации». 54

7.1 Цель работы.. 54

7.2 Порядок работы.. 54

Лабораторная работа №8 «Идентификация на основе авторегрессионных моделей» 57

8.1 Цель работы.. 57

8.2 Порядок работы.. 57

8.3 Содержание отчета. 58

Лабораторная работа №9 «Идентификация при помощи пакетов расширения MATLAB» 60

9.1 Цель работы.. 60

Лабораторная работа №10 «Оценивание состояния системы дискретным фильтром Калмана». 63

10.1 Цель работы.. 63

10.2 Порядок работы.. 63

Рекомендуемая литература. 65

Приложение А. Основы работы в MATLAB.. 67

Общие сведения. 67

Приложение Б. Виртуальный лабораторный комплекс «Моделирование и идентификация объектов управления». 72

Приложение В. Пример проверки адекватности математической модели динамики объекта с применением расчетов в среде Mathcad. 79

Приложение Г. Пример проверки адекватности математической модели статики объекта по критерию Фишера в среде Mathcad. 80

Приложение Д. Пример проверки значимости коэффициентов математической модели статики объекта по критерию Стьюдента в среде Mathcad. 81

Лабораторная работа № 8. 83

Введение

Курс «Моделирование и идентификация объектов управления (МИОУ)» является обязательным предметом для студентов высших учебных заведений и включается в учебные планы в качестве общепрофессиональной дисциплины.

Целью преподавания дисциплины является разработка математической модели и реализация процесса идентификации автоматизируемого технологического процесса (ТП), а основной задачей - построение модели по результатам наблюдений, которая являлась одной из основных задач теории автоматического управления.

Задачи преподавания дисциплины. В процессе обучения студенты должны получить

· знания:

- принципов системного подхода;

- основных методов и алгоритмов;

- особенностей исследований непрерывных и дискретных технических систем и объектов управления;

- основных положений автоматизации как научных, так и промышленные исследований в задачах идентификации и моделирования технических систем,

· умения:

- ориентироваться и обоснованно применять методы и алгоритмы;

- проводить исследования и обрабатывать результаты с целью получение математических моделей в рамках процесса проектирования и построение систем управления объектами различной физической природы;

· навыки:

- решения творческих, исследовательских и производственных задач на основе самостоятельности освоения и проработки технического задания на разработку;

- изучения литературы;

- применение вычислительной техники для реализации разрабатываемых или осваиваемых алгоритмов.

Общие указания к выполнению лабораторных работ и правила техники безопасности

Лабораторные работы предусмотрены учебным планом при изучении курса «Моделирование и идентификация объектов управления». В процессе выполнения лабораторных работ от студента требуется: закрепить теоретический материал курса, получить практические навыки в разработке математических моделей объектов управления, овладеть техникой проведения экспериментального исследования на виртуальной установке, а также приобрести навыки в оценки и интерпретации результатов эксперимента.

Работы носят исследовательский характер и выполняются каждым студентом индивидуально с использованием комплекса программ, реализующих виртуальные лабораторные установки и расчетов с применением персональных компьютеров.

Варианты исходных данных для каждого студента генерируются на основе номера зачетной книжки.

При выполнении практикума студенты используют виртуальный лабораторный комплекс «Моделирование и идентификация объектов управления» (см. приложение Б) разработанный на кафедре «Автоматизация, телекоммуникация и управление» ЮКГУ [22]. Комплекс выполнен как интерактивная система на языке программирования Delphi и представляет собой программный диалоговый комплекс позволяющий обеспечить выполнение работ №1-5.

Использование этого программного комплекса позволяет проводить эксперимент и снимать статические и динамические характеристики виртуального технологического объекта (индивидуально для каждого студента); знакомиться с теоретическими основами изучаемого метода; изучать методику проведения эксперимента и обработки его результатов; проверять результаты расчетов, выполненных вручную и др. На основание полученных расчетных данных студент выполняет расчеты вручную с использованием изучаемой методики и персонального компьютера. Программный комплекс содержит подробную справочную систему.

Ниже приведены описания лабораторных работ, посвященных современным методам идентификации динамических объектов. В лабораторных работах описываются непараметрические и параметрические методы идентификации и их реализация в среде MATLAB [19-20]. Рассматриваются как средства встроенного пакета System Identification Toolbox, так и алгоритмы, реализация которых возможна с применением любого языка высокого уровня. Кроме вопросов идентификации рассматриваются вопросы моделирования и анализа линейных систем в среде MATLAB.

Перед выполнением лабораторной работы студенты должны знать теоретическую часть данного раздела курса, чтобы отчетливо представлять цель и содержание выполняемой работы, должны быть знакомы с элементами техники безопасности и обязаны строго их выполнять.

В приведенных ниже методических указаниях для каждой работы приводятся порядок их выполнения, оформления и защиты.

После выполнения лабораторных работ, предусмотренных учебным планом, проводится зачет. Студенты, являясь на собеседование к преподавателю для получения зачета, должны представить все отчеты по лабораторным работам.

По каждой лабораторной работе студент должен:

- хорошо изучить теоретический и практический материал, по данным опыта.

- грамотно объяснить методику эксперимента и обработки его результатов и правила использования виртуальных лабораторных работ

- знать порядок проведения опыта.

- проанализировать все полученные результаты.

- сделать заключение и выводы по выполненной работе.

Задания. При расчетах и компьютерном моделировании студент использует индивидуальные исходные данные, генерируемые используемой программой для ПК на основе трех последних цифр номера зачетной книжки. Требуется введение шестизначного кода, первые три цифры кода произвольные цифры. Например если три последних цифры номера зачетной книжки 764, то вводится код 111764. По результатам работы необходимо оформить и защитить отчет.

Отчет по практикуму выполняется каждым студентом индивидуально в соответствии с дополнительно выдаваемым шаблоном. теоретических сведений и результатов, полученных из опыта.

Отчеты по выполненной лабораторной работе представляются преподавателю на следующем занятии. Студенты, не представившие отчетов по выполненным работам и не подготовившиеся к очередному занятию, к выполнению следующей работы не допускаются.

Общие правила к оформлению работ. Содержание отчета:

- общий для всех работ титульный лист;

- наименование лабораторной работы, ее цель, постановку задачи исследования;

- краткое изложение теоретических основ;

- структурную схему объекта;

- описание хода эксперимента;

- таблицу экспериментальных данных;

- таблицы и графики, иллюстрирующие обработку экспериментальных данных, конечные формулы аппроксимирующих зависимостей, значения погрешности аппроксимации и т.п.

- выводы.

Контроль выполнения лабораторных работ. Преподаватель должен контролировать все этапы работ. Результатом этого является еженедельное проставление баллов в соответствии с графиком рейтинг-контроля студента. Перед допуском к выполнению очередной работы студент сдает допуск, при этом преподаватель делает опрос студента по вопросам:

- цель работы и постановка проблемы;

- теоретические основы;

- ход эксперимента;

- методика ручных расчетов;

- выводы о полученных результатах.

По завершении работы студент оформляет отчет и защищает полученные результаты.

Правила техники безопасности и охраны труда. Особых требований по технике безопасности при выполнении лабораторного практикума не предъявляется. Необходимо строго выполнять требования инструкций по технике безопасности, вывешенные в компьютерном классе. При возникновении затруднений при работе персонального компьютера студент обращается к преподавателю и дежурному оператору компьютерного класса.

Лабораторная работа №1 «Идентификация параметров статической характеристики объекта»

1.1 Цели и задачи работы

Целью работы является определение параметров регрессионной модели. Студент должен уметь применить знания, полученные при изучении темы «Построение моделей статики объекта управления по данным пассивного эксперимента (регрессионный анализ)». Литература [1-10]

1.2 Содержание работы

Теоретические основы.

Пусть имеется объект с несколькими входами и одним выходом:

Рисунок 1.1. Структурная схема объекта

Идентификацию объекта начинают с определения статической характеристики. Подготовка к проведению эксперимента по снятию статической характеристики состоит в изучении конструкции и технологических режимов работы объекта, выбора входного (регулирующего) воздействия, стабилизации (если это возможно) источников помех. Затем выявляются минимальная Хmin и максимальная Хmax границы изменения входной координаты объекта и устанавливается минимально допустимое по технологическому режиму значение Xmin=X1. После окончания переходного процесса tпп, вызванного X1, на выходе объекта устанавливается значение Y1. Далее дается приращение входной координате X, формируется значение сигнала , который и подается на вход объекта. Спустя время tпп, регистрируется установившееся значение выхода Y2 и т.д. В результате проведения М опытов получается некоторая таблица соответствия между Xq и Yq (q=1,2,…,N).

Таким образом при исследовании статики этого объекта экспериментатор должен через определенные промежутки времени давать приращение ΔXi входной переменной Xi, поддерживая постоянными другие входные переменные. Т.е. Xi последовательно изменяется от Ximin до Ximax. При этом производится регистрация выходной переменной Y. В результате эксперимента получают статическую характеристику в виде таблиц соответствия между различными значениями X и значением Y.

Целью обработки эксперимента является аппроксимация полученной в табличной форме зависимости некоторым аналитическим выражением F(x).

Для метода приближения характерна минимизация некоторого функционала характеризующего различие между F(X)-Y(X) на всем диапазоне изменения независимой переменной Xi. На практике чаще всего используется квадратичное приближение при котором минимизируемый функционал имеет вид:

В практических расчетах функционал примет вид:

(1.1)

Для определения коэффициентов Al необходимо продифференцировать (1.1) по каждому из этих коэффициентов и приравнять к нулю полученные уравнения. Тогда мы получим систему из (m+1) уравнений, из которых мы сможем определить искомые коэффициенты:

k = 0,1,2,...,m

(1.2)

(1.3)

Рассмотрим метод наименьших квадратов для функции линейного вида F(X) = A+B·X

Адекватность полученной модели можно проверить определением средней относительной ошибки в каждой из экспериментальных точек:

(1.4)

- степенная функция –

Линеаризация проводится логарифмированием,

(1.5)

Сделаем замены:

; ;

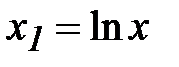После этого уравнение регрессии становится линейным:

;

где: Y(Xi) - экспериментальные точки,

F(Xi) - значения, полученные по модели

Если ε окажется менее 3-5%, то можно утверждать, что модель адекватно описывает экспериментальные данные.

Несколько иначе обстоит дело с регрессиями нелинейными по оцениваемым параметрам, которые делятся на два типа: нелинейные модели внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием) и нелинейные модели внутренне нелинейные (к линейному виду не приводятся).

К внутренне линейным моделям относятся

- степенная функция –

Линеаризация проводится логарифмированием,

(1.5)

Сделаем замены: ; ; .

После этого уравнение регрессии становится линейным:

;

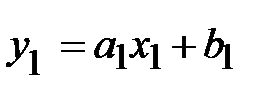- показательная – ,

- экспоненциальная –

Чтобы уравнение стало линейным, нужно убрать из показателя степени коэффициент b. Единственный способ — это сделать – логарифмировать обе части равенства:

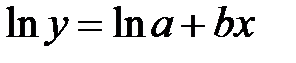(1.6)

Сделаем замены: ; ; .

После этого уравнение регрессии становится линейным:

Нужно пересчитать исходные данные для фактора Y, и потом, когда коэффициенты регрессии будут найдены, вернуться назад к коэффициентам .;

- логистическая –

- обратная –

К внутренне нелинейным моделям можно, например, отнести следующие модели:

, .

Среди нелинейных моделей наиболее часто используется степенная функция 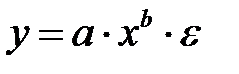, которая приводится к линейному виду логарифмированием:

, (1.7)

где 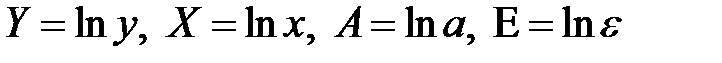. Т.е. МНК мы применяем для преобразованных данных:

а затем потенцированием находим искомое уравнение.

Таблица 1.1 Линеаризация моделей

Название функции	Вид модели	Заменяемые переменные	Вид линеаризованной модели
Показательная		Ln y = Ln a+ х ln b	Ln y = Y, Ln a = α, Ln b =β	Y = a + xb
Степенная		Ln y = Ln a+ b ln x	Ln y = Y, Ln a = α, Ln x =x	Y = a + bx
Гиперболическая		Y = a + b/x	1/x=X	Y = a +b X

Рассмотрим далее функции вида (1.8), которые являются нелинейными как по параметрам, так и по переменным:

. (1.8)

Мы обнаружим, что соотношение (1.8) может быть преобразовано в линейное уравнение путем использования логарифмов.

Применение логарифмов

Основные правила гласят:

Если у = xz, то log у = log x + log z-

Если у = x/z, то log у = log х – log z.

Если у = хп, то log у – n log х

Эти правила могут применяться вместе для преобразования более сложных выражений. Например, возьмем уравнение (1.8). Если то по правилу 1:

log у = log а + log x и по правилу 3

= log a + log х.

Для натуральных логарифмов справедливо еще одно правило:

4. Если у = ex, то log у = х.

Выражение ех, которое часто записывается как exp (x), известно также как антилогарифм х. Можно сказать, что log () является логарифмом антилогарифма х, и так как логарифм и антилогарифм взаимно уничтожаются, неудивительно, что log (е ) превращается просто в х.

Используя приведенные выше правила, уравнение (1.8) можно преобразовать в линейное путем логарифмирования его обеих частей. Если соотношение (4.4) верно, то

logy = log = log a + logx (1.9)

Если обозначить у’= log у, z = log х и a'= log а, то уравнение (1.8) можно переписать в следующем виде:

у'=а'+βz. (1.10)

Процедура оценивания регрессии теперь будет следующей. Сначала вычислим у' и z для каждого наблюдения путем взятия логарифмов от исходных значений. Вы можете сделать это на компьютере с помощью имеющейся статистической программы. Затем оценим регрессионную зависимость у' от z. Коэффициент при z будет представлять собой непосредственно оценку β. Постоянный член является оценкой а', т. е. log а. Для получения оценки а необходимо взять антилогарифм, т. е. вычислить ехр (а’).

1.3 Оборудование, технические и инструментальные средства

Для выполнения работы необходим персональный компьютер с установленной операционной системой MsWindows. Используется программа для ПК «LAB1. Виртуальная лабораторная работа №1 по дисциплине МИОУ. Определение статической характеристики объекта» или виртуальный лабораторный комплекс «Моделирование и идентификация объектов управления» (см. приложение Б).

1.4 Порядок выполнения работы

Методика проведения эксперимента:

Запустите программу LAB1, зарегистрируйтесь используя номер своей зачетной книжки.

Выберите канал, по которому будет сниматься статическая характеристика (Y = f(T), Y = f(Q) или Y = f(F)).

Разбейте интервал варьирования входной переменной на 10-15 равных частей.

Последовательно изменяя значение входной переменной от минимального до максимального, регистрируйте значение выходной переменной Y.

Выполните все необходимые расчеты вручную или с использование систем MsExcel или Mathcad.

Аналогичным образом проведите серию опытов для других входных переменных.

Выполните все необходимые расчеты вручную или с использование систем MsExcel или Mathcad.

1.5 Контрольные вопросы

- В чем отличие регулярных методов построения математических моделей от статистических?

- Что такое статическая характеристика?

- В чем отличие статической характеристики объекта от динамической?

- Методика проведения эксперимента по снятию статической характеристики.

- В каком виде может быть представлена статическая характеристика?

- Методы аппроксимации экспериментальных данных. Их достоинства и недостатки.

- Метод интерполирования.

- Метод квадратичного приближения.

- Линеаризация аппроксимирующих зависимостей.

- Проверка адекватности полученных в результате аппроксимации математических моделей.

1.6 Контрольный пример

В результате эксперимента по снятию статической характеристики, отражающей зависимость концентрации целевого продукта (Y,%) от температуры в химическом реакторе (T, °С), была получена статическая характеристика в табличной форме:

T
Y	65.06	56.39	50.3	45.79	42.32	39.56	37.32	35.46	33.9	32.56	31.4

Требуется аппроксимировать экспериментальные данные аналитическими зависимостями видов:

1)y = A+B·x

2)y = A·xB

3)y = A·10x·B

4)y = 1/(A+B·x)

5)y = x/(A+B·x)

6)y = A+B·lg(x)

7)y = A+B/x

Для определения коэффициентов А и В воспользуемся (1.2), (1.3), а для нахождения критерия адекватности уравнением (1.4). Для этого предварительно (если необходимо) линеаризуем аппроксимирующие зависимости путем замены переменных, а затем вычислим нужные суммы:

1) y = A+B·x: y = y, x = x

ΣXi= 2717; ΣYi= 470.06; ΣXi2= 682099; ΣXiYi = 112720.02

A = 118.737 B = -0.3077

2) y = A·xB; y = lg(y); x = lg(x)

ΣXi= 26.28; ΣYi= 17.812; ΣXi2= 62.82; ΣXiYi = 42.49

A = 531127.371 B = -1.7186

3) y = A·10x·B: y = lg(y), x = x

ΣXi= 2717; ΣYi= 17.812; ΣXi2= 682099; ΣXiYi = 4366.33

A = 232.432 B = -0.00302

4) y = 1/(A+B·x): y = 1/y, x = x

ΣXi= 2717; ΣYi= 0.27079; ΣXi2= 682099; ΣXiYi = 68.6744

A = -0.01559 B = 0.00016

5) y = x/(A+B·x): y = 1/y, x = 1/x

ΣXi= 0.04529; ΣYi= 0.27079; ΣXi2= 0.00019; ΣXiYi = 0.001084

A = -9.639 B = 0.0643

6) y = A+B·lg(x): y = y, x = lg(x)

ΣXi= 26.28; ΣYi= 470.06; ΣXi2= 62.82; ΣXiYi = 1116.89

A = 462.93 B = -175.884

7) y = A+B/x: y = y, x = 1/x

ΣXi= 0.04529; ΣYi= 470.06; ΣXi2= 0.00019; ΣXiYi = 1.9945

A = -9.639 B = 0.0643

Рассчитанные по модели значения выхода (Yp) и соответствующие этим моделям значения критерия адекватности можно свести в таблицу:

Таблица1.1

T	Yp1	Yp2	Yp3	Yp4	Yp5	Yp6	Yp7
	58,12	60,52	59,07	62,77	65,06	59,37	60,62
	55,04	55,59	55,10	57,05	56,39	55,59	56,05
	51,97	51,26	51,40	52,27	50,30	51,99	51,90
	48,89	47,44	47,95	48,24	45,79	48,55	48,11
	45,81	44,05	44,73	44,78	42,32	45,25	44,64
	42,74	41,03	41,72	41,79	39,56	42,10	41,46
	39,66	38,33	38,92	39,17	37,32	39,07	38,52
	36,58	35,89	36,30	36,86	35,46	36,15	35,80
	33,50	33,69	33,87	34,81	33,90	33,34	33,28
	30,43	31,70	31,59	32,97	32,56	30,63	30,93
	27,35	29,89	29,47	31,32	31,40	28,02	28,75

I	6,31	3,06	4,13	3,50	0,01	5,26	4,13

Из приведенной таблицы видно, что наиболее оптимальным образом экспериментальные данные описывает модель вида:

y = x/(A+B·x)

Аналитические зависимости, описывающие эксперимент можно представить графически (см. рисунок 2.1)

Рисунок 1.2. Пример графиков с результатами расчетов лабораторной работы №1

Лабораторная работа №2 «Однофакторный дисперсионный анализ объекта»

2.1 Цели и задачи работы

Целью работы является проверка гипотезы о равенстве математических ожиданий для каждой конкретной серии опытов. Студент должен уметь применить знания, полученные при изучении темы «Определение параметров регрессионной модели. Однофакторный дисперсионный анализ объекта управления». Литература [1-10]

2.2 Содержание работы

Теоретические основы:

В любом эксперименте среднее значение наблюдаемых величин меняется в связи с изменением входных факторов, определяющих условия эксперимента, а также и случайных факторов (помех).

Исследование влияния тех или иных факторов на изменчивость средних значений является задачей дисперсионного анализа.

Дисперсионный анализ состоит в выделении и оценке отдельных факторов, вызывающих изменчивость изучаемой случайной величины. Для этого производится разложение суммарной выборочной дисперсии на составляющие, обусловленные независимыми факторами.

Для того чтобы определить значимо ли влияние данного фактора необходимо оценить значимость соответствующей выборочной дисперсии в соответствии с дисперсией воспроизводимости, обусловленной случайными факторами.

Предположим, что результат эксперимента зависит от некоторого одиночного фактора А, который принимает n различных значений (n-количество серий опытов). Для каждой серии опытов проводится m повторных наблюдений, результаты которых можно записать в следующем виде:

Y11 Y12 Y13... Y1m

Y21 Y22 Y23... Y2m

Y31 Y32 Y33... Y3m

...............

Yn1 Yn2 Yn3... Ynm

На основе полученных статистических данных требуется проверить гипотезу о равенстве математических ожиданий для каждой конкретной серии. Если проверяемая гипотеза верна, то средние арифметические значения для всех серий практически не отличаются друг от друга, в противном случае предполагаемая гипотеза должна быть отвергнута.

Обозначим через среднее значение i-й серии опытов, а через общее среднее значение для всех наблюдений:

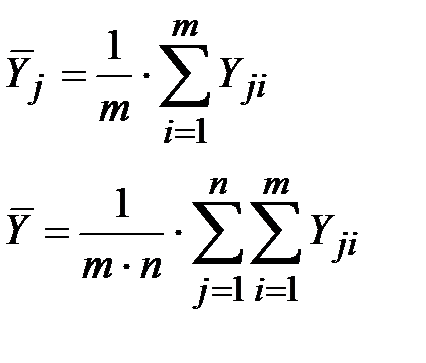
(2.1)

Сущность дисперсионного анализа состоит в разложении суммы квадратов отклонений отдельных Yij от общего среднего на две суммы:

Q - определяет общее отклонение значения каждого опыта (Yij) от среднего;

Q_А - характеризует рассеяние, вызванное фактором А (выражение во вторых фигурных скобках);

Qост - характеризует рассеяние вызванное случайными помехами (выражение в первых фигурных скобках).

Разделив суммы квадратов отклонений на соответствующие степени свободы получим следующие дисперсии:

σ² = Q/f

σ_А²= Q_A/f1 (2.2)

σ_ОСТ² = Qост/f2

Число степеней свободы f = m·n -1 f1 = n - 1 f2 = n·(m-1)

Проведение дисперсионного анализа состоит в сравнении оценок σА2и σ_ОСТ². Если гипотеза о том, что математические ожидания для каждой серии равны, верна, то σ_А² не должна существенно превышатьσ_ОСТ², что проверяется по критерию Фишера:

F = σ_А²/σ_ОСТ² (2.3)

Если F < Fкр, то различие между σ_А² и σ_ОСТ² можно считать несущественным, т.е. влияние фактора А сравнимо с влиянием случайных помех.

Если F > Fкр, то различие между σ_А² и σ_ОСТ² существенно, т.е. фактор А оказывает влияние на выходную величину.

Значение Fкр определяют по квантилям распределения Фишера, при уровне значимости α ("альфа") и степеням свободы f₁ и f₂:

Fкр = f(α, f1, f2)

2.3 Оборудование, технические и инструментальные средства

Для выполнения работы необходим персональный компьютер с установленной операционной системой MsWindows. Используется программа для ПК «LAB2. Виртуальная лабораторная работа №2 по дисциплине МИОУ. Однофакторный дисперсионный анализ объекта» или виртуальный лабораторный комплекс «Моделирование и идентификация объектов управления» (см. приложение Б).

2.4 Порядок выполнения работы

Методика проведения эксперимента:

Запустите программу LAB2, зарегистрируйтесь используя номер своей зачетной книжки.

Выберите исследуемый фактор (Y=f(T), Y=f(Q) или Y=f(F)).

Разбейте интервал варьирования входного фактора на 5-8 равных частей (уровней).

Последовательно изменяя значение входной переменной от минимального до максимального, регистрируйте значение выходной переменной Y, не забывая при этом проводить на каждом уровне серию повторных опытов (5-8).

Выполните все необходимые расчеты вручную или с использование систем MsExcel или Mathcad.

Аналогичным образом проведите эксперименты по снятию данных для других входных факторов.

Выполните все необходимые расчеты вручную или с использование систем MsExcel или Mathcad.

2.5 Контрольные вопросы:

- Что такое случайная величина?

- Виды случайных величин?

- Что такое генеральная совокупность?

- Что такое случайная выборка?

- Какая выборка называется репрезентативной?

- Что называется законом распределения, функцией распределения и плотностью распределения случайной величины?

- Что такое математическое ожидание и что оно характеризует?

- Что такое дисперсия и что она характеризует?

- Что такое среднее квадратичное отклонение (стандарт) и что оно характеризует?

- В чем состоит сущность однофакторного дисперсионного анализа?

- Методика снятия экспериментальных данных при однофакторном дисперсионном анализе?

- Что характеризует остаточная дисперсия и как она определяется?

- Как определяется дисперсия выходной величины, вызванная влиянием внешнего фактора?

- По какому критерию определяется значимость входного фактора?

2.6 Контрольный пример

В результате эксперимента по исследованию влияния фактора “Расход сырья (F)” на концентрацию целевого продукта (Y, %), была получена следующая зависимость:

Таблица2.1.

F	Y1	Y2	Y3	Y4	Y5	Y6
0,52	67,53	68,90	61,20	65,23	66,88	63,87
0,72	39,51	37,08	37,15	41,32	38,75	39,81
0,92	29,19	25,88	25,62	24,20	30,73	28,80
1,12	21,13	19,12	25,89	22,19	17,43	26,37
1,32	14,84	19,77	23,27	20,22	22,30	22,63
1,52	16,90	20,74	17,90	13,09	17,00	21,42

Требуется определить значимо ли влияние входного фактора F на выходную величину Y:

1)Количество серий - 6;количество повторных опытов - 6

2)Q_А = 9782.78, f_A = 5 (см. 2.1)

Qост = 241.84, f_ост = 30

4) σ_А² = 1956.56 (см. 2.2)

σ_ост² = 8.06

5)Расчетное значение критерия Фишера: F = 242.71 (2.3)

6)Так как F > Fkp(α, f_A, fост)=2.5 (при α = 0.05), фактор оказывает значимое влияние на выход.

7)Зависимость между F и Y можно представить графически:

Рисунок 2.1. Пример графиков с результатами расчетов лабораторной работы №2

Лабораторная работа №3 «Статистическая оценка параметров распределения случайных величин. Проверка гипотез»

3.1 Цели и задачи работы

Целью работы является проведение статистической оценки параметров распределения. Студент должен уметь применить знания, полученные при изучении темы «Определение параметров регрессионной модели. Статистическая оценка параметров, проверка гипотез». Литература [1-10]

3.2 Содержание работы

Теоретическ

Воспользуйтесь поиском по сайту: