 |
Применение функции подбора параметра при работе с диаграммами
|
|
|
|
Средство подбора параметра применяется и при работе с диаграммами. Как это делается, показано в следующем примере.
На основании данных о суммах выручки от продажи изделий в три региона нужно построить с помощью мастера диаграмм гистограмму (рис. 8) В интерактивном режиме с использованием мыши нужно настроить высоту полосы «Среднее», и посмотреть, как Ехсе1 изменит высоту полосы «Северск» для получения целевого значения. Далее необходимо дважды щелкнуть на последней полосе (один раз - для выбора ряда, а второй — для выбора полосы из ряда), которая представляет средние значения, и увеличить ее высоту путем перетаскивания маркеров размеров.
Когда кнопка мыши будет отпущена, откроется диалоговое окно “Подбор параметра. В поле “Установить в ячейке” появится имя ячейки В5, а в поле “Значение” — число, соответствующее последнему значению, которое отображалось в поле подсказки. Курсор ввода будет находиться в поле “Изменяя значение ячейки”, поэтому остается лишь ввести в данное поле значение В2. Нужно щелкнуть на кнопке ОК, после чего появится диалоговое окно “Результат подбора параметра”, в котором будет содержаться нужная информация. Щелкнуть на кнопке ОК для возврата на рабочий лист. В ячейках уже содержатся новые значения и что в соответствии с ними настроена высота полос гистограммы (рис. 9).
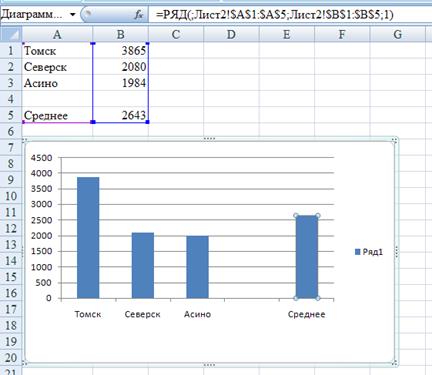
Рисунок 8 - Гистограмма “В ыручка от продажи изделий в трех регионах”

Рисунок 9 - Гистограмма “Выручка от продажи изделий в трех регионах” c применением подбора параметров
Задача: Вычисление радиуса описанной окружности по трем сторонам треугольника с помощью подбора параметра
Вычисляем радиус описанной окружности R по формуле:
|
|
|
=a*b*c_/(4*S)
где а = 2, b = 4, с_ = 5 – стороны треугольника
S – площадь треугольника
Площадь треугольника S вычисляется по формуле Герона:
= КОРЕНЬ(p*(p-a)*(p-b)*(p-c_))
где а = 2, b = 4, с_ = 5 – стороны треугольника
р – полупериметр треугольника
Полупериметр треугольника p вычисляем по формуле:
=(a+b+c_)/2
Пример вычисления радиуса описанной окружности в программе Excel показан на рисунке 10
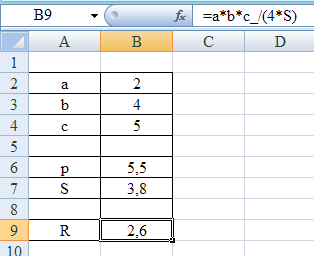
Рисунок 10 - Вычисление радиуса описанной окружности по трем сторонам треугольника
Итак, радиус описанной окружности R по трем сторонам треугольника а, b, с вычислен. Если зафиксировать длины сторон b и с, то можно считать, что R вычисляется как функция а. Но Ехсе1 дает возможность решить обратную задачу: по заданному R вычислить а. При этом не нужно решать вручную громоздкую задачу отыскания а как функции R. Формул на рабочем листе для этой цели вполне достаточно. Например, надо определить величину а при R = 3. Для это нужно выделить ячейку В9, в которой вычисляется R. В меню нужно выбрать "Сервис/ Подбор параметра". Выводится диалоговое окно "Подбор параметра". Поле "Установить в ячейке:" уже содержит адрес выделенной ячейки B9. В поле "Значение:" нужно ввести 3. В поле "Изменяя значение ячейки:" нужно ввести адрес ячейки В2, содержащей величину стороны а (если щелкнуть мышью по этой ячейке, то в поле ввода окажется адрес $В$2). После нажатия кнопки "ОК" выводится новое окно "Результаты подбора параметра". Если увеличить разрядность числа в ячейке B9, то можно увидеть, что R достигло значения 2.9999172. При этом а = 1.515753171.
Результаты выполнения показаны на рисунке 11
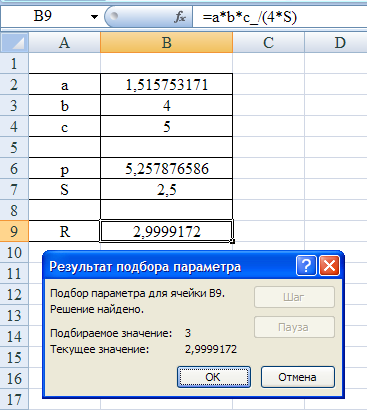
Рисунок 11 - Вычисление радиуса описанной окружности по трем сторонам треугольника с помощью подбора параметра
Единственное ли значение a соответствует R = 3? На этот вопрос изложенный метод подбора параметра не дает ответа.
|
|
|
Заключение
Список используемой литературы
1. Справка MS Excel
2. Microsoft Office Excel 2003. Учебный курс / В. Кузьмин, - СПб.: Питер: Издательская группа BHV, 2004. – 493 с.
3. Excel 2003. Эффективный самоучитель / В.В. Серогородский, - СПб.: Наука и техника, 2005. – 400 с.
4. Excel: Сборник примеров и задач / С.М. Лавренов, - М.: Финансы и статистика, 2003. – 336 с.
|
|
|


