 |
Охват модели ЖСЗ обратной связью по положению
|
|
|
|
Структура модели ЖСЗ с единичной обратной связью по положению представлена на рисунке 3, ее переходная характеристика – на рисунке 4, вид которой соответствует консервативному звену. Такая САУ находится на границе устойчивости и неспособна привести объект в конечное положение.


Охват модели ЖСЗ обратной связью по скорости и по положению

Структура модели ЖСЗ с обратной связью по скорости с фиксированным коэффициентом передачи и единичной обратной связью по положению изображена на рисунке 5. На рисунке 6. представлен график переходной характеристики системы при задающем ступенчатом воздействии в 30º.
Из переходной характеристики видно, что система, охваченная двумя обратными связями, приобретает устойчивость с приемлемыми параметрами регулирования: перерегулирование составляет примерно 3,3 %, а время регулирования – около 17 с. Установившееся значение выходного угла соответствует заданному.

Общее выражение передаточной функции структуры на рисунке 5 имеет вид:
 .
.
Определим величину коэффициента обратной связи по скорости при заданных коэффициентах демпфирования  . Очевидно что:
. Очевидно что:
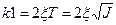 .
.
Тогда:


Для возможности изменения коэффициента демпфирования в линию местной обратной связи вводится регулятор с изменяемым коэффициентом передачи K и тогда структура модели приобретает вид, изображенный на рисунке 7.
Оценка влияния изменения коэффициента обратной связи по скорости на переходную характеристику системы
Построим переходные характеристики для двух значений k1, определенных в п.п. 3. Графики этих кривых представлены на рисунках 8 и 9.
|
|
|
Как видно из рисунков 8 и 9 увеличение коэффициента передачи сигнала обратной связи по скорости приводит к уменьшению перерегулирования и увеличению времени регулирования системы.


Определение коэффициентов обратных связей САУ при известном времени окончания переходного процесса
Если задано время переходного процесса в системе: 0,3 с, при отсутствии задающего воздействия, то можно определить коэффициенты обратных связей САУ из соображений:

где k 1, k 2 – коэффициенты обратных связей по скорости и положению соответственно; t р – время регулирования; λ1 – один из корней характеристического уравнения системы.
Если принять второй корень характеристического уравнения равным:  , то получим:
, то получим:


На рисунке 10 приведена структура САУ, удовлетворяющей заданным условиям, а на рисунке 11 – ее переходная характеристика. В модели САР множитель J выделен в отдельный блок.

Система с чистым запаздыванием. Оценка динамических свойств системы с различными временами задержки

Структура модели ЖСЗ со звеном запаздывания изображена на рисунке 12.

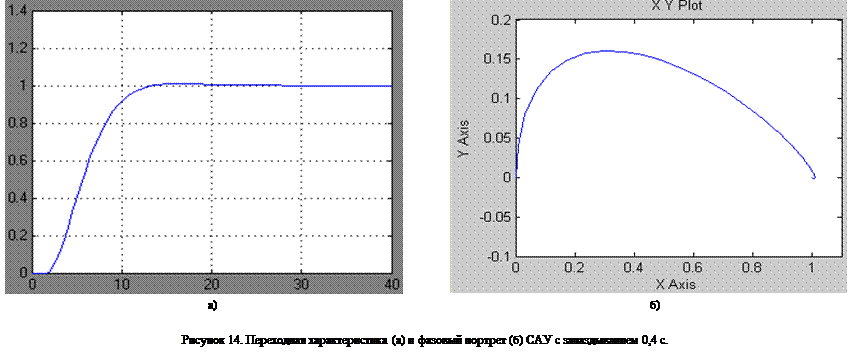
Ни рисунках 13, 14 и 15 приведены переходные характеристика и фазовые траектории САУ с запаздыванием  ,
,  и
и  соответственно.
соответственно.
Очевидно, что запас устойчивости уменьшается и ухудшаются показатели регулирования САУ со звеном запаздывания, вплоть до полной неустойчивости системы при увеличении времени запаздывания (рис. 15).
Выводы
Исследование модели ЖСЗ показало, что САУ ЖСЗ является неустойчивой в разомкнутом состоянии. В ведение единичной обратной связи по положению переводит систему на колебательную границу устойчивости и конечное угловое положение объекта управления не определено. Система становится устойчивой и управляемой при введении местной обратной связи по угловой скорости. Такая система обладает приемлемыми показателями качества регулирования и способна отрабатывать задания на угловые перемещения. Введение дополнительного регулятора в канал местной обратной связи позволяет управлять демпфированием системы, что было показано. САУ с чистым запаздыванием может быть как устойчивой с приемлемыми показателями качества регулирования, так и неустойчивой. Увеличение времени запаздывания ведет к усилению колебательных свойств системы и переходу ее в неустойчивое состояние.
|
|
|

|
|
|


