 |
Прямая общего положения. Следы прямой
|
|
|
|
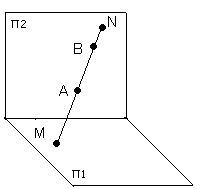
Рис. 20. Изображение прямой общего положения АВ
Прямая, не параллельная и не перпендикулярная ни одной из плоскостей проекций, называется прямой общего положения. Если прямую продолжить в обе стороны, то она пересекает плоскости проекций.
Точки пересечения прямой с плоскостями проекций называются следами прямой, причем точка пересечения с горизонтальной плоскостью проекций называется горизонтальным следом прямой, с фронтальной плоскостью проекций - фронтальным следом, а с профильной - профильным следом прямой.

Рис. 21. Построение следов прямой АВ на эпюре: горизонтального (М1, М2) и фронтального (N1, N2).
Определение действительной величины отрезка и углов наклона прямой линии к плоскостям проекций
Отрезок прямой общего положения проецируется на плоскости проекций не в натуральную величину, а с искажением. Проекция отрезка в данном случае всегда меньше его действительной величины.
При построении действительной величины отрезка можно определить углы наклона прямой, которая задана этим отрезком, к плоскостям проекций П1, П2, П3.
Чтобы определить действительную величину отрезка и угол его наклона к плоскости проекций, необходимо построить прямоугольный треугольник, одним катетом которого является проекция отрезка на плоскость, а другим - разность координат концов отрезка до плоскости проекций. Гипотенуза треугольника выражает действительную величину отрезка, а угол между ней и катетом – проекцией отрезка, выражает угол наклона отрезка к этой плоскости проекций.
Чтобы построить натуральную величину отрезка АВ, нужно на горизонтальной плоскости проекций под прямым углом от точки А или В отложить разность координат концов отрезка до горизонтальной плоскости П1. Такой координатой, измеряющей расстояние от точки до П1, является координата Z. Разность координат:
|
|
|
Z(В) – Z(А) = ΔZ
Отложив под прямым углом к А1В1 ΔZ, получим точку В0. Отрезок А1В0 выражает натуральную величину отрезка, а угол α между проекцией отрезка А1В1 и его натуральной величиной - угол наклона прямой, заданной отрезком АВ к горизонтальной плоскости проекций (рис. 22).

Рис. 22. Определение длины отрезка и угла наклона α прямой АВ к горизонтальной плоскости проекций
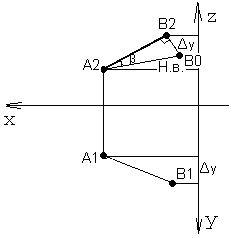
Рис. 23. Определение длины отрезка и угла наклона β прямой АВ к фронтальной плоскости проекций
Прямые частного положения
Прямые, параллельные одной или двум плоскостям проекций, называются прямыми частного положения.
Прямые, параллельные одной плоскости проекций, называются линиями уровня.
Прямая, параллельная горизонтальной плоскости проекций называется горизонтальной прямой уровня. Если прямая параллельна П1, то фронтальная проекция этой прямой параллельна оси проекций ОХ, а горизонтальная проекция отрезка этой прямой равна по величине самому отрезку А1В1 = АВ. По чертежу (рис. 24) можно определить угол наклона β горизонтальной прямой к фронтальной плоскости проекций.

Рис. 24. Горизонтальная прямая уровня
Фронтальная прямая параллельна фронтальной плоскости проекций, поэтому отрезок такой прямой проецируется в натуральную величину на П2. Угол наклона этой прямой к горизонтальной плоскости проекций обозначен на чертеже через α (рис. 25).
Профильная линия уровня параллельна профильной плоскости проекций.

Рис. 25. Прямая фронтального уровня

Рис. 26. Профильная прямая уровня
Прямые, параллельные двум плоскостям проекций, называются проецирующими.
|
|
|
Горизонтально проецирующая прямая параллельна фронтальной и профильной плоскостям проекций и, соответственно, перпендикулярна горизонтальной плоскости проекций. Она совпадает с направлением проецирования на горизонтальную плоскость проекций и поэтому имеет на П1 вырожденную проекцию прямой – точку. Натуральная величина отрезка может быть определена по фронтальной или профильной проекциям.

Рис. 27. Горизонтально проецирующая прямая
Прямая, параллельная горизонтальной и профильной плоскостям проекций, называется фронтально проецирующей. Она перпендикулярна П2 и проецируется на нее в точку, отрезок проецируется в натуральную величину на П1 и П3.

Рис. 28. Фронтально проецирующая прямая
Прямая, параллельная горизонтальной и фронтальной плоскостям проекций называется профильно проецирующей прямой. Она перпендикулярна профильной плоскости проекций П3, отрезок проецируется в натуральную величину на П1 и П2.

Рис. 29. Профильно проецирующая прямая
|
|
|


