 |
Методы измерения длины материала и анализ возникающих погрешностей
|
|
|
|
Измерение длины тканей производят непосредственно методом оценки, т. е. линейкой, рулеткой, которые непосредственно показывают измеряемую величину.
Измерения длины тканей подразделяют на технические и лабораторные, Технические измерения выполняют в производственных условиях. Перед выполнением технических измерений должна быть определена возможная погрешность. Если величина погрешности не превышает задаваемых допустимых пределов, то такие отклонения в измерениях не учитывают. В случае появления погрешностей свыше заданных допусков технологический процесс измерения должен быть перестроен.
При выполнении лабораторных измерений их погрешность должна обязательно учитываться.
Лабораторные измерения выполняют с точностью до 1 мм мерительными инструментами с минимальной ценой деления 1 мм. За длину образца при лабораторных измерениях принимают среднее арифметическое трех измерений, подсчитанное с точностью до 0,1 мм и округленное до 1,0 мм.
При технических измерениях длину ткани определяют однократным замером.
Согласно положениям математической статистики результаты измерений могут содержать погрешности: грубые (промахи), систематические, допустимые приборные, случайные.
Грубые погрешности возникают из-за невнимательности работающего, в результате чего появляются неправильные отсчеты, записи, подсчеты. Наличие грубых погрешностей определяется «выскакивающими» показателями, которые или исправляют, или исключают при обработке экспериментальных данных.
Систематические погрешности появляются при работе на неисправном оборудовании, приборах и др. Эти погрешности также называют неслучайными погрешностями, так как их появление не вызвано случайной причиной, а является следствием недостатков применяемого оборудования или инструмента. Величины таких погрешностей направлены в одну сторону и изменяются по определенному известному закону. Систематические погрешности устраняют путем тщательной проверки и наладки приборов, соблюдением методов испытаний. Случайные погрешности возникают от различных неподдающихся учету факторов. Величины случайных погрешностей направлены то в одну, то в другую сторону и могут быть различны. Абсолютная величина случайной погрешности не превосходит некоторой величины, называемой предельной погрешностью.
|
|
|
Случайные погрешности нельзя исключить введением постоянных поправок. При оценке измерений величину случайной погрешности необходимо учитывать.
Таким образом, при тщательно поставленных экспериментах остаются два вида ошибок, которые необходимо обязательно учитывать при статистической обработке экспериментальных данных.
К таким ошибкам относят допустимые погрешности, в которые входят и случайные погрешности, и допустимые приборные погрешности.
Приборные погрешности — это наибольшие погрешности прибора или инструмента, используемого при измерении. В рассматриваемом случае такими инструментами являются мерительные линейки или рулетки. Величина абсолютной погрешности равна цене одного деления принятой шкалы измерения.
Следовательно, при технических измерениях погрешность измерения равна ± 1 см, при лабораторных ± 1 мм.
В метрологических характеристиках промерочно-разбраковочного оборудования и других технических систем, предназначенных для входного контроля материалов и их настилания, обычно приводятся данные об их разрешающей способности по точности измерения. Однако в публикациях по этим вопросам отсутствует в необходимой мере анализ физической природы и количественная оценка составляющих погрешностей, возникающих при преобразовании линейных перемещений, обработке и передаче результатов измерения по информационным каналам.
|
|
|
Объективная оценка и достижение нормативной точности измерения линейных перемещений возможны при всестороннем анализе причин, порождающих систематические и случайные погрешности, включая влияние на результаты измерения физико-механических свойств обрабатываемых легкодеформируемых материалов. Для каждого класса, группы или конкретной технической системы, реализующей тот или иной способ измерения длины материалов в рулоне (куске), перечень факторов влияния может быть разным, так как каждое устройство, обладающее существенной новизной, обязательно имеет свои отличительные особенности - таковы условия признании нового технического решения изобретением.
Анализ процессов контактного взаимодействия легко деформируемых материалов с транспортирующими органами и элементами преобразователей линейных перемещений показывает, что точность измерения их длины зависит от выбранного метода, конструктивных параметров измерительной системы, напряженно-деформированного состояния, плотности, влажности и других физико-механических свойств самого материала в момент измерения. Эти факторы полностью или частично, но практически всегда, имеют место, порождая составляющие погрешностей вне зависимости от способа измерения и в ныне действующих разновидностях регистрациионно- измерительных систем.
Однако при реализации косвенного способа измерения появляются и дополнительные факторы влияния, которые необходимо учитывать при оценке погрешностей измерения длины материала. К ним относятся: условия контактного взаимодействия материала с элементами преобразователя линейных перемещений, если таковые используются; положение материала в пространстве движения и отклонение его от условно заданной линии транспортирования; влияние допусков на изготовление конструктивных элементов; способов получения, обработки, передачи, регистрации результатов измерения и т. д.
Наибольший интерес с точки зрения практической значимости предлагаемых технических решений представляют собой средства, у которых в качестве движителя полотна используется транспортёрная (мерная) лента, а в качестве преобразователя линейных перемещений - оптоэлектронная система с блоками динамической коррекции результатов измерения по стационарной или подвижной эталонной мере длины.
|
|
|
Линейные размеры кусков и в частности ширина материала, оказывая влияние на потери, являются ее важной характеристикой. Понимание этого нашло отражение в работах, посвященных исследованию ширины ткани. В них в основном рассматривается разноширинность и подчеркивается важность более полного использования ткани по ширине как фактора экономии.
Ввиду этого для швейных предприятий остается актуальной проблема учета разноширинности кусков и использования всей фактической (а не расчетной) площади ткани с целью снижения потерь сырья. Эта проблема неразрешима без разработки соответствующих методов и средств измерения ширины ткани.
Существенное влияние на экономное использование ткани оказывает способность ее к растяжению. Изменение длины материала в кусках под действием различных динамических растягивающих нагрузок на технологических операциях ПРП и в процессе хранения приводит к заведомым ошибкам при подготовке материала к раскрою, так как фактическая его длина в большинстве случаев отличается от зарегистрированной при входном контроле. Впоследствии это дает увеличение нерациональных остатков при настилании и раскрое, а также деформацию деталей кроя.
Анализ изменений линейных размеров материала в рулонах показал что следствием деформаций, происходящих при сматывании ткани в рулон и хранении, является усадка в настиле и крое. Установлено, что остаточная деформация в результате сматывания тканей в рулоны и последующего хранения в течение 24-72 ч составляет 0,2-1,5% в зависимости от приложенных нагрузок и артикула материала; период релаксации растет с увеличением нагрузки.
При проведении сравнительного анализа способов и средств измерения линейных параметров для ткани. Установлено, что браковочно-промерочные машины и трехметровые механизированные столы не обеспечивают измерения длины куска с точностью, предусмотренной стандартом. Общим недостатком этих машин является то, что измерение длины производится при неустановившемся режиме и переменном (пульсирующем) натяжении ткани. Для обеспечения точности определения линейных размеров ткани в соответствии с требованиями стандартов предлагается применять бесконтактный метод измерения, выполнять измерительные операции и проверять качество ткани в различных зонах машины, не зависящих друг от друга.
|
|
|
Таким образом, погрешности измерения длины ткани на машинах различных конструкций, как и на трехметровом столе, могут колебаться в некоторых пределах и достигать существенных значений. Они более всего определяются физико-механическими свойствами ткани и менее — конструктивными особенностями машин, хотя влияние последних не исключается.
Частные погрешности измерения длины материалов в общем случае можно объединить в следующие четыре основные группы:
• Погрешности, возникающие вследствие напряженно-деформированного состояния материала в момент его измерения, условий и параметров контактного взаимодействия с измерительным элементом, колебаний толщины, точности изготовления элементной базы и стабильности ее характеристик во времени;
• погрешности, порождаемые дискретностью преобразования перемещений в длину и пороговой чувствительностью элементной базы системы измерении;
• группа погрешностей, порождаемых отклонением материала относительно условно заданной линии его движения;
• группа погрешностей, генерируемых действием системы корректирования результатов измерения, если её использование предусмотрено в измерительной схеме.
Перечисленные первичные погрешности по своей природе носят как систематический, так и случайный характер, многие из них трудно прогнозируемы, но их необходимо учитывать при оценке точности измерения длины материала и искать пути устранения. Например, при выполнении предиз-мерительной подготовки материалов необходима релаксация их деформации, что может быть достигнуто снятием напряжений при достаточном временном сдвиге между свободным положением материала на мерной ленте и началом его измерения на прямолинейном участке движения.
Случайную же погрешность от проскальзывания материала относительно мерного элемента при использовании косвенного метода измерения без введения специальной системы корректирования результатов учесть практически невозможно. Для решения этой задачи необходима жесткая синхронизации скоростей движения материала и элемента измерения, т.е. их постоянное равенство или постоянство соотношения. Эти условия могут быть достигнуты разными методами, и в частности, посредством реализации постоянной кинематической связи между движителем и материалом.
|
|
|
Сформулируем общий подход к анализу частных погрешностей измерения длины при использовании преобразователей линейных перемещений с элементами транспортирования материала, выполненных в виде гибких звеньев-движителей. Одновременно рассмотрим и методику расчёта частных погрешностей, определяемых допусками на исполнение элементов конструкции системы измерения (параметров транспортерной ленты, приводного барабана и цены деления оптического обтюратора), а также разнотолщинностью и отклонением материала от условно заданной линии движения.
При работе преобразователя линейных перемещений с использованием гибкой транспортерной ленты (далее "мерной ленты") и перемещении её посредством приводного барабана возможны следующие варианты контактного взаимодействия между элементами измерительной системы «барабан -мерная лента - материал» (рис. 8):
а). Система «барабан - мерная лента - материал» движется синхронно, как единое целое. Между ее элементами нет проскальзывания, а силы сцепления мерной ленты с поверхностью приводного барабана превышают силы, порождающие отрицательную деформацию ее приграничного слоя вследствие изгиба контактного участка материала (рис. 8 а, б);
б). Подсистема элементов «мерная лента - материал» движется синхронно, как единое целое, а силы сцепления между поверхностью барабана и мерной лентой исключают возможность отрицательных деформаций её приграничных слоев, но допускают их относительное скольжение (рис. 8, в);
в). Элементы подсистемы «мерная лента - материал» движутся без относительного скольжения. Тангенциальные силы, определяющие изгибной момент и отрицательную деформацию слоев мерной ленты, расположенных ниже нейтральной линии на участке контакта, превышают силы сцепления, обеспечивающие передачу движения мерной ленте без скольжения. Также допускается, что подсистема элементов этого участка в начале и конце границ контактного взаимодействия не проскальзывает относительно барабана, а приграничные с ним слои участка ленты вследствие изгиба на цилиндрической поверхности испытывают отрицательную деформацию (рис. 8, г);
г). Элемент системы «материал» проскальзывает относительно мерной ленты на участке их контакта, определяемого углом обхвата, а участок ленты 'взаимодействует с приводным барабаном согласно пункту "б" или "в";
д). Все элементы системы «барабан - мерная лента - материал» на поверхности, определяемой углом обхвата, взаимодействуют с относительным скольжением.

Рис. 8 – Схема взаимодействия элементов системы “барабан - мерная лента - материал” при транспортировании материала и измерении его длины:1- транспортерная (мерная) лента; 2- материал; 3- схваты; 4- приводной барабан; 5- система считывания угла поворота барабана.
Исходя из условий первого в порядке рассмотрения варианта контактного взаимодействия элементов системы, можно с определенными допущениями предположить, что подсистема «мерная лента - материал» при взаимодействии с приводным барабаном испытывает деформации изгиба и частичного растяжения, а в результате наложения этих деформаций приграничный с барабаном слой ленты имеет нулевое растяжение.
В этом случае линия прямолинейного участка подсистемы, движущаяся со скоростью Va, задается окружной скоростью приводного барабана и должна иметь нулевое значение деформаций.
При этом скорости Vb, Vc и Vd точек b, с, d (см. рис. 8,б), принадлежащие соответственно мерной ленте и материалу, равные на прямолинейном участке движения между собой и скорости Vа изменятся (увеличатся) при контакте с барабаном и будут зависеть от его радиуса и угла обхвата. В этом случае приращение скоростей точек b, с, d на участке обхвата компенсируется деформацией элементов подсистемы «мерная лента - материал».
Так как движителем материала является мерная лента, то окружная скорость (Vокp) её точек на границе контакта с барабаном при угловой скорости = const будет равна Vокp= Va= R.
Истинное перемещение и соответственно длина материала на этом участке определяется длиной дуги окружности барабана радиуса r =R, т.е. зависит от радиуса контактного взаимодействия, при котором отсутствует деформация слоев мерной ленты, граничащих с поверхностью барабана.
Исходя из условий рассматриваемой задачи, в приграничном слое взаимодействия подсистемы «мерная лента - материал» с барабаном перемещение (S) будет отражать фактическое значение длины материала т. е.
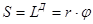 (1)
(1)
где - угол поворота приводного барабана и жёстко связанного с ним оптического обтюратора.
Дифференцируя выражение (1) по параметру r и заменяя дифференциалы малыми конечными приращениями, получим значение частной погрешности () от точности изготовления приводного барабана ()т.е.
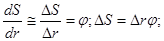
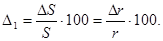 (2)
(2)
Из выражения (2) видно, что абсолютная погрешность преобразования перемещения в длину накапливается с увеличением угла поворота, а относительная ошибка пропорциональна величине допуска () и обратно пропорциональна номинальному радиусу приводного барабана (r).
Рассмотрим второй, теоретически и практически возможный вариант контактного взаимодействия элементов системы «барабан - мерная лента - материал».
При скольжении мерной ленты относительно приводного барабана возникает некоторая неопределенность погрешности преобразования перемещения в длину. Величина проскальзывания имеет случайный характер и поэтому оценить длину материала по углу поворота приводного барабана и точность измерения практически не представляется возможным. В этом случае необходимы дополнительные технические решения или исключающие скольжение элементов подсистемы, или обеспечивающие требуемую коррекцию погрешности результатов измерений, порождаемую этим явлением.
Дадим аналитическое исследование третьего, и наиболее вероятного, варианта контактного взаимодействия элементов подсистемы «мерная лента - материал» с приводным барабаном (см. рис. 8,г). В этом случае значение радиуса R, определяющего линию нулевой деформации и истинное перемещение длины материала, с учетом конкретных условий можно определить, если воспользоваться соотношением упругих деформаций растяжения и сжатия подсистемы «лента - материал» относительно нейтральной оси.
Согласно [8], учитывая принятые условия контактного взаимодействия и делая допущение того, что подсистема «лента - материал» испытывает на поверхности барабана изгиб, как балка прямоугольного сечения, получим:
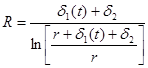 , (3)
, (3)
где - толщина мерной ленты без учёта монтажных (начальных) деформаций; - толщина материала.
Выражение (3) запишется в виде:
 (4)
(4)
где
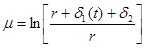 (5)
(5)
Тогда с учетом (1):
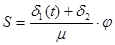 (6)
(6)
Если выражение (6) для фиксированных моментов времени, т.е. при продифференцировать в частных производных по каждому параметру и согласно линейной теории точности [9,10] заменить дифференциалы их малыми приращениями, чем, по сути, они являются, получим:
 (7)
(7)
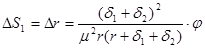
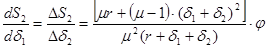 (8)
(8)
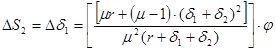
Аналогично (8)
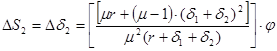 (9)
(9)
Максимальные абсолютная и относительная погрешности от рассмотренной группы первичных погрешностей соответственно равны:
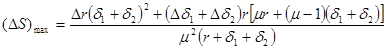 (10)
(10)
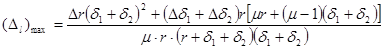 (11)
(11)
Выражения (10, 11) позволяют количественно оценить влияние отклонений на погрешность измерения и в зависимости от требуемой точности выбрать конструктивные параметры и назначить допуски на их проектирование.
Частные погрешности измерений, обусловленные отклонениями линейных параметров звеньев измерительной системы от номинальных, подчиняются определённым законам и их можно учесть введением соответствующих поправок в результаты измерения.
Теоретический анализ четвертого и пятого вариантов контактного взаимодействия элементов системы не представляет практического интереса вследствие их взаимного скольжения и появления предпосылок значительных и неопределенных погрешностей измерения перемещения мерной ленты и материала по углу поворота барабана. В этом случае задача должна и может быть решена посредством поиска принципиально новых технических решений, которые обеспечивали бы в процессе движения материала его постоянное сцепление с движущейся транспортёрной лентой.
Следующим конструктивно-технологическим фактором, влияющим на точность измерения длины, является несовпадение в процессе измерения линии начала и конца отсчёта с метками оптического обтюратора. Это возможно вследствие случайностей взаимного положения поперечных срезов в начале и конце полотна с метками диска или не кратности длины рулона их количеству. Величина этой погрешности хотя и является случайной, но не повторяется при непрерывном измерении, и её максимальное значение не превышает длины дуги, определяемой двумя делениями оптического диска, т.е.,где - цена деления диска.
Так как перемещение (длина материала) оценивается по измеренной длине дуги линии нулевой деформации подсистемы "мерная лента - материал", то
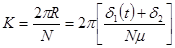 (12)
(12)
где К - коэффициент передачи измерительной системы; N - число меток оптического обтюратора.
Тогда для действительной длины материала в рулоне ():
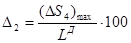 (13)
(13)
Таким образом, при проектировании измерительной системы для повышения её точности согласно выражениям (9, 13) необходимо уменьшать разнотолщинность мерной ленты и материала, цену деления обтюратора и увеличивать диаметр приводного барабана.
Отдельным вопросом стоит определение погрешности измерения длины материала при его перекосе относительно условно заданной линии движения. Так как эту группу погрешностей можно уменьшить только посредством качества центрирования полотна или равнения по его кромке (полностью исключить влияние этого фактора на точность измерения не представляется возможным), то необходимо вводить и эту частную составляющую в общую оценку погрешности расчётным путём.
Проанализируем зависимость погрешности измерения длины материала от качества его ориентации, т.е. от наличия некоторого периодически повторяющегося отклонения полотна относительно условно заданной линии движения (рис. 9).

Рис. 9 – Расчетная схема определения погрешности измерения длины материала от перекоса линии движения
Согласно расчётной схеме абсолютная погрешность измерения от несовпадения кромки с заданной линией движения будет равна:

где п - количество возможных отклонений линии движения материала от условно заданной; - абсолютная ошибка измерения длины материала на i-ом участке движения.
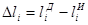
где -соответственно фактически измеренное и действительное значения длины i-ro участка рулона.
Но 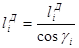 (14)
(14)
где - угол перекоса заданной линии движения полотна на i-ом участке рулона.
Тогда:
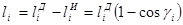 (15)
(15)
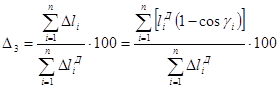 (16)
(16)
Согласно (14) и (16)
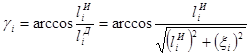 (17)
(17)
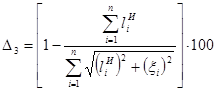 (18)
(18)
где - величина отклонения кромки материала от условно заданной линии движения на i-ом отрезке рулона.
Из выражения (18) видно, что погрешность измерения длины материала при перекосе линии его движения зависит от величины отклонения и угла наклона оси () валика системы ориентации, определяющего количество этих отклонений (n). Значение в общем случае будет являться нестационарной величиной, зависящей от конструктивных характеристик системы транспортирования, технологических параметров и режимов взаимодействия контактирующих сред.
Экспериментальные исследования показали, что отклонение положения материала в пространстве движения без равнения его по кромке или центрирования перед измерением может нарастать с переходом процесса поперечного перемещения в неустойчивый режим, практически ограничиваемый только размерами «створа» системы транспортирования полотна. Поэтому перед измерением длины движущегося материала необходимо обеспечивать технологически заданное его отклонение от контрольной линии, что и достигается системой ориентации.
Таким образом, исследования точности измерения длины движущегося материала с использованием динамической коррекции и без нее позволяют сделать общий вывод в пользу этого варианта построения измерительной схемы. Наличие системы корректирования позволяет исключать как систематические, так и значительно уменьшать составляющие случайных погрешностей, возникающие от возможного неконтролируемого скольжения подсистемы "мерная лента - материал" относительно барабана (мерного диска), от влияния температурно-влажностного фактора, наличия люфтов в механической части системы и т.д.
Для достижения требуемой точности измерения корректировку можно выполнить и программными средствами, внося поправки в количество импульсов, приходящихся на эталонную длину, "покачивая" коэффициент корректирования, а также вводя более жесткие допуски на размеры элементов конструкции преобразователя линейных перемещений, уменьшая пену деления обтюраторного диска и, соответственно, коэффициент передачи К.
Теоретический анализ частных погрешностей, рассмотренная методика расчёта точности преобразования линейных перемещений и результаты исследований характеристик измерительных систем позволяют определить комплекс мер по улучшению метрологических характеристик технологического оборудования, выбрать направление его совершенствования и дать конкретные рекомендации по расчёту, проектированию и эксплуатации.
|
|
|


