Динамический гаситель с учетом демпфирования

Динамический гаситель без учета демпфирования

 

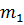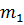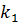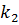Для упрощения здесь рассматривается система с двумя степенями свободы. Часть системы с массой является основной. Использование динамического гасителя основано на присоединении к основной системе, имеющей массу и жесткость упругой связи , дополнительной массы гасителя , связанной с основной массой упругой связью с жесткостью (рис. 51). Демпфированием системы пренебрегаем.

Основная система приводится в колебательное движение возмущающей силой.

Дифференциальные уравнения колебания полученной системы с двумя степенями свободы (сложение переносного и относительного движений) имеют вид:

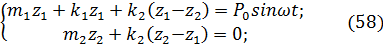
где и — абсолютные координаты перемещений масс 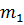и .

Частные решения этой системы уравнений, соответствующие установившимся колебаниям, определяются выражениями:

Здесь С₁ — амплитуда колебаний объекта массой 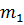, С₂ — амплитуда колебаний динамического гасителя массой . После подстановки частных решений в систему уравнений (58) получим

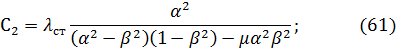
В формулах (60) и (61):

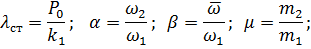
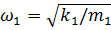- круговая частота собственных колебаний объекта (при отсутствии гасителя), - парциальная круговая частота собственных колебаний гасителя (при неподвижной массе ).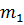

Из выражения (60) видно, что основная масса 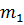не будет совершать колебания (С₁=0) при , когда круговая частота 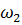гасителя будет равна круговой частоте 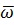возмущающей силы:

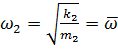(62)

При этом хотя возмущающая сила и действует на массу 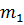, однако она вызывает колебания только дополнительной массы , Амплитуда этих колебаний, как это следует из формулы (61), при будет равна:

Очевидно, что при правильном подборе и настройке масса динамического гасителя колеблется в противофазе как раз с такой амплитудой, что сила, с которой пружина жесткостью 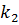действует на основную массу 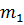, уравновешивает возмущающую силу, передающуюся на эту массу через пружину жесткостью k₁. Таким образом, присоединение к объекту гасителя, настроенного на частоту возмущающей силы, образует систему с двумя степенями свободы, у которой при частоте, совпадающей с частотой возмущающей силы, возникает антирезонанс.

При использовании динамического гасителя для систем пассивной виброзащиты необходимо уменьшить амплитуду колебаний защищаемого объекта от вибрации его основания с амплитудой С_осн. При этом, с учетом формулы (63), для настройки можно использовать зависимость

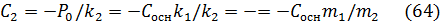
Расчет динамического гасителя без демпфирования связан с необходимостью удовлетворять ряду ограничений. Подбор жесткости С₂ упругого элемента (или массы ) должен обеспечивать и его прочность. Кроме того, следует учитывать, что присоединенная масса в системах пассивной виброзащиты должна составлять не менее 1-2% от массы защищаемого объекта.

При настройке динамического гасителя на антирезонанс по обе стороны от частоты настройки гасителя (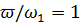) возникают дополнительные резонансные частоты. Поэтому системы с гасителем без демпфирования, настроенные на антирезонанс, очень чувствительны к изменению частоты возмущающей силы ц или жесткости упругого элемента k₂. Любая незначительная настройка гасителя может привести к резкому увеличению амплитуды и свести «на нет» весь эффект от антирезонанса.

Динамический гаситель с учетом демпфирования

 

Для того, чтобы гаситель был эффективным в достаточно широкой области частот возмущающей силы, необходимо между основным объектом с массой т и гасителем с массой ввести дополнительный демпфер с коэффициентом вязкости 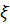. Для таких гасителей, называемых гасителями с затуханием, существуют определенные значения коэффициента настройки частот β, при которых можно «настроить» гаситель таким образом, что амплитуда колебаний всей системы не будет зависеть от характеристики демпфера. Такой гаситель называется гасителем с наилучшей настройкой.

Для его «настройки» на любую величину массы гасителя должно выполняться условие

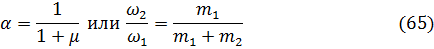
Амплитуда колебаний объекта в случае активной виброзащиты при этом будет равна

Для динамических гасителей с демпфированием при постоянной настройке, т.е. когда 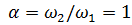, собственная частота 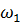и амплитуда С₁ колебаний объекта массой 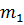при выбранной массе гасителя находятся из соотношений:

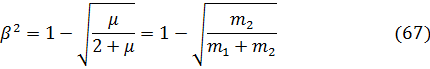
В этом случае гаситель называют настроенным на частоту системы. Коэффициент затухания в демпфере, удовлетворяющий условию наилучшего действия гасителя, определяется по известной формуле

где: 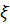- относительный параметр затухания. Параметр затухания можно также определять по приведенным здесь аппроксимационным формулам:

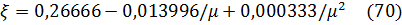
Формула (70) соответствует гасителю с наилучшей настройкой, а формула (71) - гасителю, настроенному на частоту основной системы.

При использовании динамического гасителя в системах пассивной виброзащиты его эффективность оценивается отношением амплитуды колебаний конструкции без гасителя к «остаточной» амплитуде колебаний конструкции после установки гасителя. Максимальная эффективность гасителя с затуханием достигается при 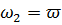и обратно пропорциональна коэффициенту вязкости 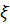, что соответствует условию

Таким образом, величина вязкости (относительного демпфирования) является определяющим параметром для динамических гасителей с затуханием, воспринимающих гармонические воздействия. Чем меньше демпфирование динамического гасителя, тем выше его эффективность при строго фиксированных частотах возмущения, так как при этом Однако даже при незначительной настройке по частоте можно получить нежелательное и даже опасное увеличение колебаний защищаемого объекта.

При проектировании гасителя для пассивной виброзащиты обычно приходится иметь дело с многочастотными (полигармоническими) колебаниями основания (фундамента), поэтому важно рассчитать такое значение коэффициента вязкости, при котором динамический гаситель будет достаточно эффективен в необходимой ширине полосы частот возмущения. Требуемый, коэффициент 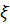может быть определен по формуле:

где 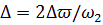- относительная ширина рабочей зоны частот возмущения (настройка гасителя); v - допускаемый коэффициент снижения эффективности гасителя за счет затухания; 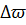-максимальная величина расстройки частоты возмущения.

Конструктивное выполнение динамических виброгасителей, применяемых в настоящее время, весьма разнообразно и зависит от вида виброзащиты (активная, пассивная), формы колебаний, характера движения рабочих органов и типа источника вибрации, а также других факторов.

Пример расчета динамического гасителя для активной виброзащиты

Требуется рассчитать динамический гаситель для поршневого компрессора весом Р₁ =2000 Н, являющегося источником вертикальных колебаний с частотой . Амплитуда возмущающей силы, создаваемой компрессором, Р_о = 500 Н. Допускаемая амплитуда колебаний компрессора [ С₁ ] = 0,8 мм, а амплитуда колебаний динамического гасителя не должна превышать 2 мм, т.е. .

Решение

Расчет гасителя без затухания

Гаситель без затухания рассчитаем для резонансного режима, т.е. при фиксированных значениях частот:

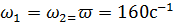
Требуемую жесткость упругого элемента гасителя найдем из формулы (64):

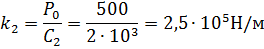
Необходимую массу динамического гасителя определим из формулы (65):

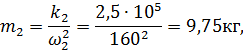
т.е. вес гасителя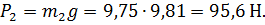

Требуемую для соблюдения резонансного режима гасителя жесткость упругих элементов, устанавливаемых между компрессором и фундаментом, найдем по формуле:

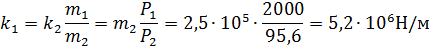
Статическая осадка этих упругих элементов

Ответ: Статическая осадка упругих элементов 0, 4 мм, что вполне допустимо.

 

Поделиться:

Воспользуйтесь поиском по сайту: