 |
Момент завинчивания, условия самоторможения и КПД
|
|
|
|
Рассмотрим силы, действующие в резьбовом соединении
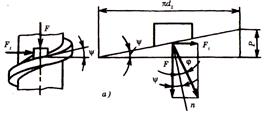
Dcр– средний диаметр трения по торцу головки или гайки;
d2 – средний диаметр резьбы;
Mk– крутящий момент на оси;
F– осевое усилие;
Ft– окружное усилие по среднему диаметру резьбы;
N – нормальное усилие взаимодействия между винтом и гайкой, вектор которого смещен на угол трения;
f – коэффициент трения в торце;
f 1 – коэффициент трения в резьбе, tgφ= f 1
Момент завинчивания гайки или винта с головкой: Тзав= Тр+Тт,
где Тр – момент в резьбе; ТT – момент трения на торце гайки или головки винта.
Момент в резьбе: Тр=Ftd2/2=F∙tg (ψ+φ)∙d2/2;
Опорную поверхность гайки и головки принимают кольцевой с наружным диаметром, равным размеру под ключ D1и внутренним диаметром, равным диаметру отверстия под винт d0. Следовательно Dcр= (D1+ d0)/2;
Момент трения на торце гайки или головки: Тт=F∙ f ∙Dcр/2;
Момент заворачивания:Тзав= F∙tg (ψ+φ)∙d2/2+F∙ f ∙Dcр/2= F∙(d2/2)∙(tg(ψ+φ)+ f ∙Dcр/d2);
Момент отвинчивания: Тотв=F∙(d2/2)∙(tg(φ-ψ)+ f ∙Dcр/d2);
Условие самоторможения в резьбе: Тотв=F∙(d2/2)∙(tg(φ-ψ)+ f ∙Dcр/d2)≥0, или tg(φ-ψ)≥0, следовательно ψ≤φ или ψ≤arctg(f 1).
При коэффициенте трения f 1=0,1 (сталь по стали); угол φ=6º, а для крепежных резьб значение угла подъема ψ лежит в пределах 2°30' – 3°30', следовательно крепежные резьбы – самотормозящие. Резьбы для ходовых винтов выполняют как самотормозящие, так и несамотормозящие.
Приведенные выше значения коэффициента трения, свидетельствующие о существенных запасах самоторможения, справедливы только при статических нагрузках. При динамических и вибрационных нагрузках вследствие взаимных микросмешений поверхностей трения коэффициент трения существенно снижается и условие самоторможения нарушается. Происходит самоотвинчивание, для избежания самоотвинчивания применяют специальные стопорные устройства.
|
|
|
КПД винтовой пары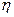 
определяется отношением работы, затраченной на завинчивание гайки без учета трения, к той же работе с учетом трения. Работа завинчивания равна произведению момента завинчивания на угол поворота гайки. Так как углы поворота равны и в том и в другом случае, то отношение работ равно отношению моментов Тзав!/Тзав, в котором Тзав= F∙(d2/2)∙(tg(ψ+φ)+ f ∙Dcр/d2); а Тзав!=F∙(d2/2)∙(tg(ψ+0)+0∙Dcр/d2), следовательно: η=Тзав/Тзав!= tg(ψ)/(tg(ψ+φ)+ f ∙Dcр/d2)
В частном случае, когда трение в опорах по торцам очень мало (на пример, если опорой являются подшипники качения): η=tg(ψ)/(tg(ψ+φ).
Расчет резьбовых соединений при различных случаях нагружения
Осевая нагрузка винта передаётся через резьбу гайке и уравновешивается реакцией её опоры. Каждый из Z витков резьбы нагружается силами F1, F2, … FZ.
В общем случае нагрузки на витках не одинаковы. Задача о распределении нагрузки по виткам статически неопределима и была решена русским учёным Н.Е. Жуковским в 1902 г. на основе системы уравнений для стандартной шестигранной гайки.
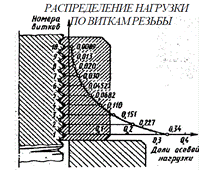
График показывает значительную перегрузку нижних витков и бессмысленность увеличения длины гайки, так как последние витки практически не нагружены.
Такое распределение нагрузки позже было подтверждено экспериментально. При расчётах неравномерность рагрузки учитывают эмпирическим (опытным) коэффициентом Km, который равен 0,87 для треугольной, 0,5 – для прямоугольной и 0,65 для трапецеидальной резьбы. Основные виды разрушений у крепёжных резьб – срез витков, у ходовых - износ витков. Следовательно, основной критерий работоспособности для расчёта крепёжных резьб – прочность по касательным напряжениям среза, а для ходовых резьб – износостойкость по напряжениям смятия.
|
|
|
Сварные соединения
|
|
|
