 |
Площадь криволинейной трапеции
|
|
|
|
Тема: Определенный интеграл.
Метод интегральной суммы.
Опр. Аддитивной величиной наз. параметр физической системы Р, который можно представить как сумму его значений от всех составных частей системы P = 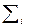 pi.
pi.
Например, площадь фигуры, объем тела, длина пройденного пути. Разбиение на составные части в этих случаях совершенно произвольно. Разделение пространственного объекта можно довести до уровня отдельной точки, затем определить в ней значение нужного параметра, но вот вычислить сумму бесконечно большого числа таких слагаемых прямым суммированием нельзя. Приходится вводить специальную процедуру суммирования “точечных” параметров - метод интегральной суммы.
 Задача. Вычислить площадь круга радиуса R.
Задача. Вычислить площадь круга радиуса R.
Строим вписанный в круг n – угольник и соединяем его вершины с центром. Тогда 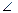 АОС = 2
АОС = 2 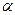 = 2
= 2  /n, AC = =2AB = 2R sin
/n, AC = =2AB = 2R sin 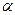 , SAOC = AB BO = Rsin
, SAOC = AB BO = Rsin 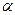 Rcos
Rcos 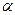 = ½ R2sin2
= ½ R2sin2 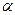 . Площадь многоугольника Sn = n SAOC в пределе n
. Площадь многоугольника Sn = n SAOC в пределе n  переходит в площадь круга S = lim Sn =
переходит в площадь круга S = lim Sn =
=½ R2 lim n sin 2  /n =
/n =  R2 lim sin(2
R2 lim sin(2  /n)/(2
/n)/(2  /n) =
/n) =  R2
R2
Последовательность действий: имеем основную фигуру, разделяем ее на n участков, вычисляем площадь одного треугольника, вычисляем общую площадь треугольников, переходим к пределу. Эта процедура носит универсальный характер.
Алгоритм метода интегральной суммы.
1. Исследуемая аддитивная система разделяется на n однотипных участков (разбиение Z).
2. Для каждого участка устанавливается некоторое приближенное значение аддитивного параметра pi.
3. Проводится суммирование приближенных значений аддитивного параметра по всем n участкам P(n) = 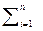 pi
pi
4. Переход к пределу lim P(n) = P при n  дает точное решение задачи, т.е. определяет значение искомого параметра для всей системы
дает точное решение задачи, т.е. определяет значение искомого параметра для всей системы
Опр. Интегральной суммой наз. сумма всех приближенных значений аддитивного параметра, определенных для каждого из n участков на которые была разделена исследуемая система.
|
|
|
Опр. Предел интегральной суммы, полученной путем разбиения пространственного объекта на составные части, наз. интегралом (определенным).Это главный параметр суммы
 Вид суммы и её предела определяется условиями задачи и числом использованных переменных. Существуют двойные, тройные, криволинейные, поверхностные интегралы.
Вид суммы и её предела определяется условиями задачи и числом использованных переменных. Существуют двойные, тройные, криволинейные, поверхностные интегралы.
Площадь криволинейной трапеции
Опр. Фигура ограниченная графиком функции y = f(x) на промежутке [a,b], осью Ох и двумя перпендикулярами, восстановленными из точек a и b наз. криволинейной трапецией.
Метод интегральной суммы:
1) Отрезок [a, b] разделим на n равных частей точками xi = a + i  x, где i = 0,1,2, …,n и
x, где i = 0,1,2, …,n и  x = (b – a)/n. Из точек xi восстановим перпендикуляры и соединим их прямыми | | оси Ох на высоте f(
x = (b – a)/n. Из точек xi восстановим перпендикуляры и соединим их прямыми | | оси Ох на высоте f( i), где xi
i), где xi 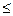
 i
i 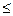 xi+1 . Получим вспомогательную, ступенчатую фигуру, составленную из прямоугольников. 2) Площадь одного прямоугольника f(
xi+1 . Получим вспомогательную, ступенчатую фигуру, составленную из прямоугольников. 2) Площадь одного прямоугольника f( i)
i)  xi. 3)Площадь всей вспомогательной фигуры, т.е. интегральная сумма, равна
xi. 3)Площадь всей вспомогательной фигуры, т.е. интегральная сумма, равна
Sn = 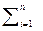 f(
f( i)
i)  xi (1)
xi (1)
Чем больше n, тем точнее приближение, а предел n  должен дать точный результат
должен дать точный результат
Опр. Определенным интегралом от функции f(x) на промежутке [a,b] наз. предел интегральной суммы, полученный путем разбиения промежутка на малые участки.
lim 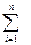 f(
f( i)
i)  xi =
xi = 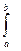 f(x) dx (2)
f(x) dx (2)
Здесь а – нижний предел, b – верхний предел, а сам символ повторяет основные элементы интегральной суммы. Введен Лейбницем.
Геометрический смысл определенного интеграла – площадь криволинейной трапе-ции. Геометрический смысл интегральной суммы – площадь вспомогательной фигуры.
Основные свойства определенного интеграла.
10  A f(x)dx = A
A f(x)dx = A  f(x)dx
f(x)dx
Постоянный множитель выносится за знак интеграла, т.к. он может быть вынесен за знак суммы.
20  [f(x) + g(x)] dx =
[f(x) + g(x)] dx =  f(x) dx +
f(x) dx +  g(x) dx
g(x) dx
Интеграл от суммы функций равен сумме интегралов, т.к. предел от суммы функций равен сумме пределов.
|
|
|
30  f(x) dx =
f(x) dx = 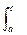 f(x) dx =
f(x) dx =  f(x) dx (a < c < b)
f(x) dx (a < c < b)
Интеграл на промежутке [a,b] можно представить как сумму интегралов, взятых по произвольным участкам [a,b]. См. геом. смысл неопр. ин-ла.
40  f(x) dx = -
f(x) dx = -  f(x) dx Замена пределов меняет общий знак. (опр.)
f(x) dx Замена пределов меняет общий знак. (опр.)
50 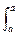 f(x) dx = 0 (нет ширины у трапеции)
f(x) dx = 0 (нет ширины у трапеции)
60 Теорема о среднем.  f(x) dx = f(
f(x) dx = f( ) (b – a)
) (b – a)
Определенный интеграл от непрерывной функции всегда можно представить как произведение полного приращения аргумента (b – a) на значение функции в некоторой промежуточной точке f( ), т.к. для любой трапеции можно построить прямоугольник такой же ширины и площади (a
), т.к. для любой трапеции можно построить прямоугольник такой же ширины и площади (a 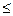

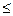 b)
b)
Пр. Вычислить площадь трапеции f(x) = xk на интервале [0, a] (k- целое число)
1) Разбиение Z. Точками xi = (a/n) i, где i = 1,2,… n с шагом  x = (a/n)
x = (a/n)
2) Площадь i – ого прямоугольника f( i)
i)  xi = (xi)k
xi = (xi)k  x = (a/n)k+1 i k
x = (a/n)k+1 i k
3) Интегральная сумма Sn = 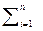 f(
f( i)
i)  xi = (a/n)k+1
xi = (a/n)k+1 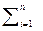 i k
i k
4) Доказано, что 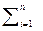 i k = nk+1 / (k+1) +
i k = nk+1 / (k+1) +  Am nk-m, где Am – коэффициенты.
Am nk-m, где Am – коэффициенты.
При переходе к пределу n  не нулевой вклад дает только первое слагаемое и площадь трапеции равна S = lim Sn = ak+1 /(k+1).
не нулевой вклад дает только первое слагаемое и площадь трапеции равна S = lim Sn = ak+1 /(k+1).
Отсюда легко получить площадь трапеции на произвольном интервале [a, b]. Достаточно записать разность площадей трапеций на интервалах [0, b] и [0,a]
Sab = bk+1/(k+1) - ak+1/(k+1)
Если вычислять площадь трапеции от произвольной функции f(x) на интервале
[0,a] методом интегральной суммы,то приходится в f(x) заменять х на (a/n)i и суммировать сложное выражение Sn = (a/n) 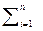 f((a/n)i), что удается в редких случаях. К счастью, существует более простой способ определения предела интегральной суммы. В последнем примере связь между исходной функцией f(x) = xk и результатом S(x) = xk+1/(k+1) оказалась простой S’(x) = f(x). Ниже покажем, что такая связь справедлива и для произвольной функции f(x).
f((a/n)i), что удается в редких случаях. К счастью, существует более простой способ определения предела интегральной суммы. В последнем примере связь между исходной функцией f(x) = xk и результатом S(x) = xk+1/(k+1) оказалась простой S’(x) = f(x). Ниже покажем, что такая связь справедлива и для произвольной функции f(x).
Определенный интеграл с переменным верхним пределом.
Такой интеграл имеет вид Ф(х) =  f(t) dt, является функцией от х и определяет площадь криволинейной трапеции переменной ширины (х – а). Возьмем производную от этой функции
f(t) dt, является функцией от х и определяет площадь криволинейной трапеции переменной ширины (х – а). Возьмем производную от этой функции
Ф’(х) = lim  Ф(х) /
Ф(х) /  x
x
 x
x  0
0
Ф(х+  x) - Ф(х) =
x) - Ф(х) = 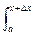 f(t)dt -
f(t)dt -  f(t)dt =
f(t)dt =  f(t)dt +
f(t)dt +  f(t)dt -
f(t)dt -  f(t)dt = f(c)
f(t)dt = f(c)  x
x
где с точка на промежутке [x, x+  x] по теореме о среднем. Перейдем к пределу
x] по теореме о среднем. Перейдем к пределу
Ф’(x) = lim  Ф(х) /
Ф(х) /  x = lim f(c)
x = lim f(c)  x /
x /  x = f(c) = f(x)
x = f(c) = f(x)
 x
x  0
0  x
x  0
0
т.е. интеграл с переменным верхним пределом является одной из первообразных для подынтегральной функции, т.к.
|
|
|
Ф’(x) = f(x) (3).
Формула Ньютона – Лейбница.
Это центральная теорема мат. анализа. Она делает замену сложной процедуры вычисления пределов интегральной суммы на процедуру вычисления первообразных.
Теорема. Определенный интеграл от непрерывной функции f(x) на промежутке [a, b] равен разности значений первообразных этой функции F(x) на концах отрезка
 f(x) dx = F(b) - F(a) (4)
f(x) dx = F(b) - F(a) (4)
Доказательство. Имеем функцию f(x), ее первообразную F(x) и строим функцию
Ф(х) =  f(t) dt, которая также является первообразной функции f(x) по условию (3). Т.о., имеем две первообразных, которые могут отличаться только на константу
f(t) dt, которая также является первообразной функции f(x) по условию (3). Т.о., имеем две первообразных, которые могут отличаться только на константу
Ф(x) = F(x) + C (5)
Значение константы С находим из (5) при x = a:
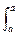 f(t) dt = F(a) + C = 0 или C = - F(a)
f(t) dt = F(a) + C = 0 или C = - F(a)
Теперь равенство (5) принимает вид  f(t) dt = F(х) - F(a) и при x = b переходит в формулу Ньютона – Лейбница (4).
f(t) dt = F(х) - F(a) и при x = b переходит в формулу Ньютона – Лейбница (4).
Вычисление работы.
Работа по перемещению тела по прямой на расстояние S под воздействием постоянной силы F равна A = F S. Сила может зависеть от величины смещения:
F = f(x). Например, силу растяжение пружины описывает закон Гука: F = k x. В этом случае расчет произведенной работы делают методом интегральной суммы.
1) Участок пути движения тела вдоль Ох от а до b разбивают на n отрезков длиной  x = (b – a) / n; 2) Работа при перемещении вдоль одного отрезка равна
x = (b – a) / n; 2) Работа при перемещении вдоль одного отрезка равна
f( i)
i)  x, где f(
x, где f( i) -среднее значение силы для i – ого отрезка; 3) Сумма по всем отрезкам равна A(n) =
i) -среднее значение силы для i – ого отрезка; 3) Сумма по всем отрезкам равна A(n) = 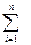 f(
f( i)
i)  x и совпадает с интегральной суммой (1); 4) Переход к пределу n
x и совпадает с интегральной суммой (1); 4) Переход к пределу n  дает точное решение задачи
дает точное решение задачи
lim 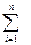 f(
f( i)
i)  xi = А =
xi = А = 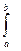 f(x) dx (1)
f(x) dx (1)
Физический смысл определенного интеграла - работа по перемещению тела в поле переменных сил.
Вычислим этот предел для случая закона Гука. Пусть  i -крайние точкиотрезков, тогда f(
i -крайние точкиотрезков, тогда f( i) = k
i) = k  i = k[a +
i = k[a +  ],
],  x =
x =  и интегральная сумма равна
и интегральная сумма равна
A(n) = k  = k (b-a) {
= k (b-a) { 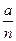
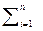 1 +
1 + 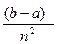
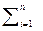 i }=
i }=
= k (b-a) { a + 
 }
}
Переход к пределу A = lim A(n) = k (b-a) { a + (b-a)/2 } = k (b2 – a2)/2
Формула Ньютона – Лейбница A = k 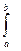 x dx = k x2/2 |ab = k (b2 – a2)/2
x dx = k x2/2 |ab = k (b2 – a2)/2
Теорема о среднем: A = k (b – a) (b + a)/2, т.е. среднее значение силы F( ) = k (b + a)/2
) = k (b + a)/2
Приемы интегрирования.
Метод замены переменной при вычислении определенного интеграла по формуле Ньютона-Лейбница требует дополнительной операции - переопределения пределов интегрирования.
|
|
|
Пр.  x2dx /(x3 + 2)2 = { t = x3+2, tн=13+2 = 3, tв= 23+2 =10, dt = 3x2dx, x2dx = dt/3}=
x2dx /(x3 + 2)2 = { t = x3+2, tн=13+2 = 3, tв= 23+2 =10, dt = 3x2dx, x2dx = dt/3}=
= 1/3  dt/t2 = - 1/3 1/t |310 = 7/90
dt/t2 = - 1/3 1/t |310 = 7/90
Формула интегрирования по частям принимает вид  u dv = u v|ab -
u dv = u v|ab -  v du (6)
v du (6)
Пр.  (x+3) sin x dx = {u = x+3, du = dx, dv = sin x dx, v = - cos x } =
(x+3) sin x dx = {u = x+3, du = dx, dv = sin x dx, v = - cos x } =
= - (x+3) cos x |0  +
+  cos x dx = 3 + sin x |0 = 4
cos x dx = 3 + sin x |0 = 4
Несобственные интегралы.
При введении определенного интеграла предполагалось, что функция f(x) ограничена, а интервал интегрирования конечен. Несобственные интегралы являются обобщением определенного интеграла на случай неограниченной функции и бесконечных пределов интегрирования.
Опр. Несобственным интегралом 1 рода (с бесконечными пределами интегрирования.) наз. предел определенного интеграла, когда его верхний, нижний предел устремляется к бесконечности
lim  f(x) dx = J
f(x) dx = J 
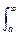 f(x) dx (7)
f(x) dx (7)
b 

Интеграл наз. сходящимся несобственным, если предел существует и расходящимся, если такой предел не существует
Пр. 
 dx / x ln x = lim
dx / x ln x = lim 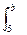 d(ln x)/ ln x = lim (ln ln b – ln ln 5) =
d(ln x)/ ln x = lim (ln ln b – ln ln 5) = 
b 
 b
b 

т.е. несобственный интеграл расходится. Если обозначить lim F(b) = F(+  ), то перейдем к обобщенной формуле Ньютона – Лейбница
), то перейдем к обобщенной формуле Ньютона – Лейбница
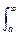 f(x) dx = F(+
f(x) dx = F(+  ) - F(a), F’(x) = f(x) (8)
) - F(a), F’(x) = f(x) (8)
Пр.  dx / x ln x =
dx / x ln x =  d(ln x)/ ln x = ln in x |5
d(ln x)/ ln x = ln in x |5  = ln ln
= ln ln  – ln ln 5 =
– ln ln 5 = 
Опр. Несобственным интегралом 11 рода (от разрывных функций) наз. предел определенного интеграла, когда его верхний, нижний предел устремляются к точке разрыва II рода
 lim
lim 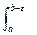 f(x) dx = J
f(x) dx = J 
 f(x) dx, где lim f(x) =
f(x) dx, где lim f(x) =  (9)
(9)
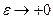 x
x  b
b
Интеграл наз. сходящимся несобственным, если предел существует и расходящимся, если такой предел не существует
Пр. Функция f(x) = 1/  при 0
при 0 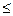 х < 1 ограничена и непрерывна, следовательно, интегрируема
х < 1 ограничена и непрерывна, следовательно, интегрируема
lim  1/
1/  dx = lim arcsin (1 -
dx = lim arcsin (1 - 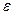 ) =
) =  /2
/2
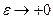
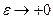
т.е. несобственный интеграл сходится. Если обозначить lim F(b - 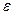 ) = F(b) при
) = F(b) при 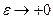 и для точки разрыва b функции f(x) (F’(x) = f(x)), то вычисление несобственного интеграла II рода проводится по обычнойформуле Ньютона – Лейбница
и для точки разрыва b функции f(x) (F’(x) = f(x)), то вычисление несобственного интеграла II рода проводится по обычнойформуле Ньютона – Лейбница
 1/
1/  dx = arcsin х |01 =
dx = arcsin х |01 =  /2
/2
Если функция f(x) на [a, b] имеет несколько точек разрыва, то в интеграле  f(x) dx = F(b) - F(a) необходимо проверить значение F(x) для всех особых точек. Только полная непрерывность F(x) обеспечивает сходимость несобственного интеграла II рода.
f(x) dx = F(b) - F(a) необходимо проверить значение F(x) для всех особых точек. Только полная непрерывность F(x) обеспечивает сходимость несобственного интеграла II рода.
Пр. Интеграл 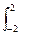 2x dx/ (x2 – 1) = ln |x2 – 1| |-22 не существует, т.к. первообразная обращается в
2x dx/ (x2 – 1) = ln |x2 – 1| |-22 не существует, т.к. первообразная обращается в  в особых точках x =
в особых точках x =  1
1
Вычисление площади плоской фигуры.
 Определенный интеграл
Определенный интеграл 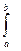 f(x) dx, при условии f(x) > 0, определяет площадь криволинейной трапеции расположенной выше оси Ох. Если f(x) < 0, то значение интеграла будет отрицательно, т.к. имеем предел суммы отрицательных слагаемых. Если f(x) пересекает ось Ох, то трапеция делится на верхние и нижние участки и интеграл равен разности их площадей. Задачу вычисления полной площади криволинейной трапеции прилежащей к оси Ох определяют формулы
f(x) dx, при условии f(x) > 0, определяет площадь криволинейной трапеции расположенной выше оси Ох. Если f(x) < 0, то значение интеграла будет отрицательно, т.к. имеем предел суммы отрицательных слагаемых. Если f(x) пересекает ось Ох, то трапеция делится на верхние и нижние участки и интеграл равен разности их площадей. Задачу вычисления полной площади криволинейной трапеции прилежащей к оси Ох определяют формулы
|
|
|
1. f(x) > 0 SD = 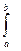 f(x) dx
f(x) dx
2. f(x) < 0 SD = - 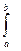 f(x) dx (10)
f(x) dx (10)
3. f(x) >< 0 SD = 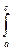 f(x) dx -
f(x) dx -  f(x) dx
f(x) dx 
4. f(x) > g(x) SD = 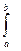 f(x) dx -
f(x) dx - 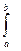 g(x) dx
g(x) dx
Пр. Вычислить площадь, ограниченную линиями y = sin x, y = 0, x = -  /2, x =
/2, x =  .
.
SD = -  sin x dx +
sin x dx + 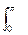 sin x dx = cos x|0-p./2 + cos x|0p = 3
sin x dx = cos x|0-p./2 + cos x|0p = 3
Если криволинейная трапеция задана в параметрической форме: x = x(t), y = y(t),
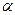
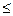 t
t 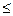
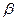 , x(
, x(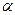 ) = a, x(
) = a, x(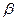 ) = b (a < b), y = 0, то переход к новым переменным дает
) = b (a < b), y = 0, то переход к новым переменным дает
SD = 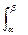 y(t) x’t dt (11)
y(t) x’t dt (11)
Пр. Вычислить площадь эллипса: x = a cos t, y = b sin t, 0 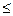 t
t 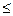 2
2 
SD = 4ab  sin2t dt =
sin2t dt =  ab
ab
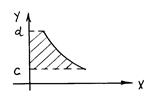 В том случае, если криволинейная трапеция прилежит к оси Оу (x = x(y), c £ y £ d), то ее площадь определяется интегралом
В том случае, если криволинейная трапеция прилежит к оси Оу (x = x(y), c £ y £ d), то ее площадь определяется интегралом
S =  x(y) dy (12)
x(y) dy (12)
 Площадь криволинейного сектора в полярных координатах.
Площадь криволинейного сектора в полярных координатах.
Площадь кругового сектора радиуса R с углом 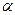 равна
равна

 =
= 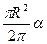 =
= 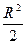
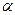 . Если r = r(
. Если r = r( ),
), 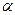
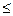

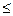
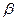 , то сектор становиться криволинейным и его площадь вычисляется методом интегральной суммы.1) Разбиение угла b -a точками
, то сектор становиться криволинейным и его площадь вычисляется методом интегральной суммы.1) Разбиение угла b -a точками  i =
i = 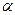 +
+ 
 i, где i =1,2,…n, с шагом
i, где i =1,2,…n, с шагом 
 = (
= ( )/n; 2) i – ый сектор заменяем на круговой сектор радиуса r(
)/n; 2) i – ый сектор заменяем на круговой сектор радиуса r( i). Его площадь r2(
i). Его площадь r2( i)/2
i)/2 
 ; 3) интегральная сумма Sn =
; 3) интегральная сумма Sn = 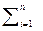 r2(
r2( i)/2
i)/2 
 переходит в интеграл SD = ½
переходит в интеграл SD = ½ 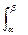 [r(
[r( )]2d
)]2d  (13)
(13)
Вычисление длины дуги.
 Имеем кривую y = f(x) на [a, b]. Определим ее длину методом интегральной суммы.
Имеем кривую y = f(x) на [a, b]. Определим ее длину методом интегральной суммы.
1) Разобьем [a, b] на n равных по длине отрезков точками xi = a + i (b – a)/n, где i = 0,1,2, …,n. Из точек xi восстановим перпендикуляры до пересечения с кривой y = f(x) и соединим отрезками l i соседние точки пересечения. В результате получим вспомогательную ломанную линию вдоль кривой; 2) Отрезок l i есть гипотенуза треугольника с катетами  xi =(b-a)/n ,
xi =(b-a)/n ,  yi = yi – yi-1 и его длина равна
yi = yi – yi-1 и его длина равна
l i = 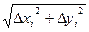 =
=  ; 3) Длина всей ломанной линии есть интегральная сумма L n =
; 3) Длина всей ломанной линии есть интегральная сумма L n = 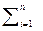
 ; 4) Переход к пределу n
; 4) Переход к пределу n  приводит к появлению производной lim
приводит к появлению производной lim  = f `(x) и дает точную длину дуги в виде определенного интеграла
= f `(x) и дает точную длину дуги в виде определенного интеграла
L = lim 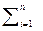
 =
= 
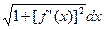 (14)
(14)
Пр. Вычислить длину линии y = 2x + 1 на промежутке [1, 3].
Решение: y’ = 2,  =
= 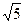 , L =
, L = 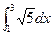 =
= 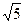 x|13 = 2
x|13 = 2 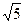
Если x = x(t), y = y(t), t1 < t < t2, то l i =  и
и
L =  (15)
(15)
Если функция задана в полярных координатах: r = r(j) – полярное уравнение,
j Î [a,b], тогда D x» d(x) = d(r(j) cos j) = [r’cos j - rsin j] dj, D y» d(y) = d(r(j) sin j) = [r’sin j + r cos j] dj, (D x)2 + ( D y)2 = [r2(j) + (r`(j))2] (dj)2 и
L = 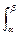
 (16)
(16)
Вычисление площади боковой поверхности и объема тела вращения.
 Криволинейную трапецию, ограниченную неотрицательной функцией y = f(x) на [a, b] вращаем вокруг оси Ох и получаем цилиндрическое тело вращения. Определим площадь его боковой поверхности и объем методом интегральной суммы.
Криволинейную трапецию, ограниченную неотрицательной функцией y = f(x) на [a, b] вращаем вокруг оси Ох и получаем цилиндрическое тело вращения. Определим площадь его боковой поверхности и объем методом интегральной суммы.
1) Вращение криволинейной трапеции предыдущего рисунка приведет к вспомогательной фигуре - последовательности усеченных конусов с радиусами оснований f(xi) и наклонными длинной l i. 2) Боковая поверхность и объем каждого такого конуса (цилиндра) равны
Si = 2  l i (f(xi) + f(xi-1)) / 2; Vi =
l i (f(xi) + f(xi-1)) / 2; Vi =  f(xi)2
f(xi)2  xi
xi
3) Просуммируем Si, Vi и получим две интегральные суммы
S(n) = 2 
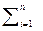 l i f(xi); V(n) =
l i f(xi); V(n) = 
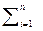 f(xi)2
f(xi)2  xi
xi
4) Переход к пределу n  дает решение задачи
дает решение задачи
Sбок = lim S(n) = 2 
 f(x)
f(x) 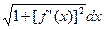 (17)
(17)
V = lim V(n) = 
 f2(x) dx (18)
f2(x) dx (18)
 Пр. Определить площадь боковой поверхности и объем кругового конуса высоты h и радиуса основания r.
Пр. Определить площадь боковой поверхности и объем кругового конуса высоты h и радиуса основания r.
Решение. Уравнение образующей y = r/h x, где 0 <x < h. Тогда y’ = r/h,  =
= 
Sбок = 2 
 r/h
r/h  x dx =
x dx =  r
r  =
=  r l
r l
V = 
 (r/h)2 x2 dx =
(r/h)2 x2 dx =  h r2 / 3
h r2 / 3
Устные экзаменационные вопросы
по теме: «Неопределенный и определенный интегралы, КЧ»
Повторение: 1) Опр. функции; 2) Опр. сложной функции, перечислить ее элементы; 3) Опр. производной по Коши и по Ньютону, её алгебраический, физический, геометрический смысл; 4) Перечислить правила дифференцирования; 5) Опр. дифференциала, правило его вычисления.
1. Опр. первообразной функции и неопределенного интеграла.
2. Перечислить названия элементов, входящих под знак неопределенного интеграла.
3. Сколько первообразных имеет каждая функция и почему?
4. Перечислить основные свойства неопр. интеграла.
5. Объяснить инвариантность формы дифференциала сложной функции и неопр ин-ла.
6. Что такое непосредственное интегрирование?
7. В чем заключается идея метода замены переменных?
8. Вывод формулы интегрирования по частям.
9. Основная теорема алгебры.
10. Опр. рациональной алгебраической дроби. Переход от неправ-ой к прав-ой дроби.
11. Записать формулу разложения рац-ой алгебр-ой дроби на сумму простых дробей.
12. Общее правило при линейной замене переменных.
13. Перечислить основные виды замены переменных в интегралах от тригон. функций.
14. Правила вычисления интегралов с линейными и квадратичными иррациональностями.
15. Опр. аддитивной величины.
16. Алгоритм метода интегральной суммы.
17. Опр. интегральной суммы.
18. Опр. криволинейной трапеции.
19. Опр. определенного интеграла. Его геометрический и физический смысл.
20. Перечислить основные свойства определенного интеграла. Теорема о среднем.
21. Опр. интеграл с переменным верхним пределом. Его вид и общее свойство.
22. Доказать формулу Ньютона-Лейбница. Ее значение в мат. анализе.
23. Опр. несобственного интеграла 1 и 2 рода. Общее правило вычисления интеграла от разрывных функций.
24. Общие правила вычисления площади плоской фигуры.
25. Площадь криволинейного сектора в полярных координатах. Записать интегральную сумму и интеграл.
26. Длина произвольной дуги. Записать интегральную сумму и интеграл.
27. Боковая поверхность и объем тела вращения. Записать интегральную сумму и интеграл.
|
|
|


