 |
Тест по теме «дифференциальное и интегральное исчисление функций одной переменной»
|
|
|
|
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
| Пределы. Теоретические вопросы. | |
| 1. | Какой вид имеет функция, называемая числовой последовательностью? |
| 2. | Если числовая последовательность является монотонной и ограниченной, то она…(вставить пропущенные слова) |
| а) | может сходиться |
| б) | может расходиться |
| в) | сходится |
| г) | расходится |
| д) | является бесконечно малой |
| 3. | Выберите верное определение предела функции «на языке  »: число »: число  называется пределом функции называется пределом функции  при при  , если…(вставить пропущенные слова) , если…(вставить пропущенные слова)
|
| а) | для любого  существует число существует число 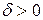 такое, что для всех такое, что для всех  , удовлетворяющих неравенству , удовлетворяющих неравенству  , выполняется неравенство , выполняется неравенство 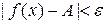 . .
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 4. | При каком условии число  называется пределом функции в точке называется пределом функции в точке  слева? слева?
|
| 5. | Для того чтобы функция  имела в точке имела в точке  предел, равный числу предел, равный числу  , необходимо и достаточно, чтобы…(вставить пропущенные слова) , необходимо и достаточно, чтобы…(вставить пропущенные слова)
|
| а) | функция  была ограниченной в некоторой окрестности точки была ограниченной в некоторой окрестности точки 
|
| б) | функция  была непрерывной в точке была непрерывной в точке 
|
| в) | в этой точке существовал предел |
| г) | функция  была бесконечно малой в точке была бесконечно малой в точке 
|
| д) | в этой точке существовали односторонние пределы функции, которые равны 
|
| 6. | Что можно сказать о функции  , если , если     ? ?
|
| 7. | В чем состоит связь между функцией, ее пределом и бесконечно малой функцией? |
| 8. | Пусть  , ,  при при  . Указать пределы, в которых возникает неопределенность. . Указать пределы, в которых возникает неопределенность.
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 9. | Пусть  , ,  при при  . Указать пределы, в которых возникает неопределенность. . Указать пределы, в которых возникает неопределенность.
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 10. | Пусть  , ,  при при  . Указать пределы, в которых возникает неопределенность. . Указать пределы, в которых возникает неопределенность.
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 11. | Пусть  и и 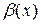 – бесконечно малые функции в точке – бесконечно малые функции в точке  , т.е. , т.е.  , , 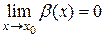 . Какие определения вводятся для сравнения бесконечно малых функций? . Какие определения вводятся для сравнения бесконечно малых функций?
|
| 12. | При каком условии две бесконечно малые в точке  функции функции  и и  являются эквивалентными? являются эквивалентными?
|
| 13. | Указать эквивалентные бесконечно малые функции в окрестности точки  . .
|
| а) |  , , 
|
| б) | 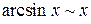 , , 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 14. | Указать эквивалентные бесконечно малые функции в окрестности точки  . .
|
| а) | 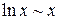
|
| б) | 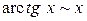 , , 
|
| в) | 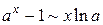
|
| г) | 
|
| д) | 
|
| 15. | Указать замечательные пределы. |
| 16. | Функция  называется непрерывной в точке называется непрерывной в точке  , если…(вставить пропущенные слова) , если…(вставить пропущенные слова)
|
| а) | она определена в точке  и ее окрестности. и ее окрестности.
|
| б) | существует  . .
|
| в) | 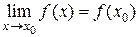 . .
|
| г) | функция является ограниченной в окрестности точки. |
| д) | 
|
| 17. | Как называется точка  , в которой функция , в которой функция  имеет предел слева и справа, причем имеет предел слева и справа, причем  ? ?
|
| 18. | Указать верные свойства функций, непрерывных в точке. |
| а) | Пусть функции  и и  непрерывны в точке непрерывны в точке  . Тогда функции . Тогда функции  , , 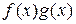 и и 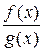 также непрерывны в этой точке (последняя при также непрерывны в этой точке (последняя при  ). ).
|
| б) | Если функция  непрерывна в точке непрерывна в точке  , а функция , а функция  непрерывна в точке непрерывна в точке  , причем , причем  , то сложная функция , то сложная функция  является непрерывной в точке является непрерывной в точке  . .
|
| в) | Чтобы функция  была непрерывной в точке была непрерывной в точке  необходимо и достаточно, чтобы она была ограниченной в некоторой окрестности точки необходимо и достаточно, чтобы она была ограниченной в некоторой окрестности точки  . .
|
| г) | Пусть функции  и и  непрерывны в точке непрерывны в точке  . Тогда функции . Тогда функции  , , 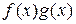 и и 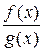 непрерывны в окрестности этой точки (последняя при непрерывны в окрестности этой точки (последняя при  ). ).
|
| д) | Если функция  непрерывна в точке непрерывна в точке  , а функция , а функция  непрерывна в точке непрерывна в точке  , причем , причем  , то сложная функция , то сложная функция  является непрерывной в окрестности точки является непрерывной в окрестности точки  . .
|
| 19. | Какие свойства имеет функция  , непрерывная на отрезке , непрерывная на отрезке  ? ?
|
| 20. | Если функция  непрерывна на отрезке непрерывна на отрезке  , ,  , то…(вставить пропущенные слова) , то…(вставить пропущенные слова)
|
| а) | на интервале  найдется хотя бы одна точка найдется хотя бы одна точка  , в которой функция обращается в нуль. , в которой функция обращается в нуль.
|
| б) | на этом отрезке она принимает все промежуточные значения между  и и 
|
| в) | функция имеет непрерывную обратную функцию |
| г) | при  на интервале на интервале  найдется хотя бы одна точка найдется хотя бы одна точка  , в которой функция обращается в нуль. , в которой функция обращается в нуль.
|
| д) | на интервале  найдется хотя бы одна точка найдется хотя бы одна точка  , в которой , в которой 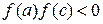 . .
|
| Пределы. Практические задания. | |
| 21. | Функция  удовлетворяет условиям удовлетворяет условиям  , ,  . Указать способ задания функции. . Указать способ задания функции.
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 22. | Чему равен предел  ? ?
|
| 23. | Чему равен предел  ? ?
|
| 24. | Чему равен предел 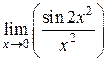 ? ?
|
| 25. | Чему равен предел  ? ?
|
| 26. | Чему равен предел  ? ?
|
| 27. | Чему равен предел  ? ?
|
| 28. | Чему равен предел 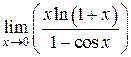 ? ?
|
| 29. | Чему равен предел  ? ?
|
| 30. | Чему равен предел  ? ?
|
| 31. | Чему равен предел  ? ?
|
| 32. | Чему равен предел  ? ?
|
| 33. | Чему равен предел  ? ?
|
| 34. | Чему равен предел  ? ?
|
| 35. | Чему равен предел  ? ?
|
| 36. | Чему равен предел  ? ?
|
| 37. | Исследовать на непрерывность функцию 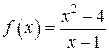 . .
|
| Дифференциальное исчисление. Теоретические вопросы. | |
| 38. | Выберите правильное определение производной функции. |
| а) | 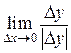
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 39. | Выберите верный вид формулы касательной к графику функции  в точке в точке  . .
|
| 40. | По каким формулам вычисляются  в точке в точке  , если функции , если функции 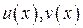 являются дифференцированными в этой точке? являются дифференцированными в этой точке?
|
| 41. | По какой формуле вычисляется производная сложной функции 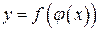 , если функция , если функция  имеет производную в точке имеет производную в точке  , а функция , а функция  – в точке – в точке  ? ?
|
| 42. | По какой формуле вычисляется производная обратной функции  в точке в точке  , если в точке , если в точке  функция функция  имеет производную имеет производную  ? ?
|
| 43. | Определить, по каким формулам вычисляются производные функций: 1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  , где , где  . .
|
| 44. | Определить, по каким формулам вычисляются производные функций: 1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  , где , где  . .
|
| 45. | Определить, по каким формулам вычисляются производные функций: 1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  , где , где  . .
|
| 46. | По какой формуле вычисляется дифференциал 1-го порядка функции  ? ?
|
| 47. | Дать определение дифференциала функции  порядка порядка   , т.е. , т.е.  . .
|
| 48. | Какому условию удовлетворяет производная  в точке в точке 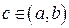 , если:
1) функция , если:
1) функция  непрерывна на непрерывна на 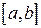 ;
2) функция ;
2) функция  дифференцирована на дифференцирована на  ;
3) ;
3)  ? ?
|
| 49. | Теорема Лагранжа. Если функция  непрерывна на отрезке непрерывна на отрезке  и дифференцируема на интервале и дифференцируема на интервале  , то на интервале , то на интервале  найдется такая точка найдется такая точка  , что имеет место формула… (вставить пропущенные слова) , что имеет место формула… (вставить пропущенные слова)
|
| 50. | Теорема Коши. Пусть функции  и и  непрерывны на отрезке непрерывны на отрезке  и дифференцируемы на интервале и дифференцируемы на интервале  , причем , причем  для всех для всех  . Тогда найдется такая точка . Тогда найдется такая точка  на этом интервале, что имеет место формула… (вставить пропущенные слова) на этом интервале, что имеет место формула… (вставить пропущенные слова)
|
| 51. | Выберите верный вид формулы Лопиталя, если  и и  в окрестности точки в окрестности точки  . .
|
| 52. | Выберите верное поведение функции  , являющейся дифференцируемой на интервале , являющейся дифференцируемой на интервале  и и  на на  . .
|
| 53. | Пусть  – точка локального максимума функции – точка локального максимума функции  . Какое неравенство выполняется для всех . Какое неравенство выполняется для всех  из некоторой из некоторой  -окрестности точки -окрестности точки  ? ?
|
| 54. | Пусть функция  имеет в точке имеет в точке  локальный экстремум и дифференцируема в этой точке. Указать необходимое условие локального экстремума функции. локальный экстремум и дифференцируема в этой точке. Указать необходимое условие локального экстремума функции.
|
| 55. | Пусть функция  дифференцируема в некоторой дифференцируема в некоторой  -окрестности точки -окрестности точки  и пусть и пусть  . Указать достаточное условие локального экстремума функции по первой производной. . Указать достаточное условие локального экстремума функции по первой производной.
|
| 56. | Пусть функция  имеет непрерывную вторую производную в окрестности точки имеет непрерывную вторую производную в окрестности точки  . Указать достаточное условие локального экстремума функции. . Указать достаточное условие локального экстремума функции.
|
| 57. | В каком случае график функции  имеет на имеет на  выпуклость, направленную вниз (функция является вогнутой)? выпуклость, направленную вниз (функция является вогнутой)?
|
| 58. | Указать необходимое условие существования точки перегиба  графика функции графика функции  . .
|
| 59. | В каком случае прямая  называется вертикальной асимптотой графика непрерывной функции называется вертикальной асимптотой графика непрерывной функции  ? ?
|
| 60. | Прямая  является наклонной асимптотой непрерывной кривой является наклонной асимптотой непрерывной кривой  при при  . По каким формулам вычисляются значения . По каким формулам вычисляются значения  и и  ? ?
|
| Дифференциальное исчисление. Практические задания. | |
| 61. | Вычислить производную функции  . .
|
| 62. | Вычислить производную функции  . .
|
| 63. | Вычислить производную функции 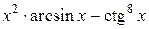 . .
|
| 64. | Вычислить производную функции  . .
|
| 65. | Вычислить производную функции 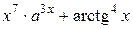 . .
|
| 66. | Найти производную 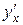 функции, заданной параметрически функции, заданной параметрически  , ,  , ,  при при  . .
|
| 67. | Какие из приведенных пределов можно вычислить только по правилу Лопиталя? |
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 68. | Найти предел  , используя правило Лопиталя. , используя правило Лопиталя.
|
| 69. | Найти предел  , используя правило Лопиталя. , используя правило Лопиталя.
|
| 70. | Найти предел  , используя правило Лопиталя. , используя правило Лопиталя.
|
| 71. | Найти предел  , используя правило Лопиталя. , используя правило Лопиталя.
|
| 72. | Найти предел  , используя правило Лопиталя. , используя правило Лопиталя.
|
| 73. | Найти уравнение наклонной асимптоты графика функции  . .
|
| 74. | Найти интервал(ы) убывания графика функции  . .
|
| 75. | Найти интервал(ы) возрастания графика функции 
|
|
|
|
|
|
|
|
|
|
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
| Неопределенный интеграл. Теоретические вопросы | |
| 1. | Какому условию должна удовлетворять первообразная  от функции от функции  на отрезке на отрезке  ? ?
|
| 2. | Чему равна разность между двумя первообразными  и и  от одной функции от одной функции  на отрезке на отрезке  ? ?
|
| 3. | Что называется неопределенным интегралом от функции  , если , если  – первообразная для – первообразная для  , а , а  ? ?
|
| 4. | Чему равна производная от неопределенного интеграла, если  является первообразной для является первообразной для  , а , а  ? ?
|
| 5. | Чему равен дифференциал от неопределенного интеграла  , если , если  является первообразной для является первообразной для  , а , а  ? ?
|
| 6. | Чему равен неопределенный интеграл от дифференциала некоторой функции  , если , если  является первообразной для является первообразной для  , а , а  ? ?
|
| 7. | Укажите верную формулировку теоремы об инвариантности формул интегрирования. |
| 8. | Чему равен интеграл  , если , если 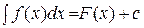 ? ?
|
| 9. | В каких формулах таблицы интегралов допущена ошибка? |
| а) | 
|
| б) | 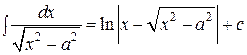
|
| в) | 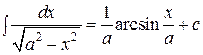
|
| г) | 
|
| д) | 
|
| 10. | Какая функция имеет производную  ? ?
|
| 11. | Какая функция имеет производную  ? ?
|
| 12. | Какая формула называется формулой интегрирования по частям неопределенного интеграла? |
| 13. | Укажите, при вычислении каких приведенных интегралов необходимо использовать формулу интегрирования по частям? |
| а) | 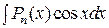 , где , где  – многочлен степени – многочлен степени 
|
| б) | 
|
| в) | 
|
| г) | 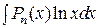 , где , где  – многочлен степени – многочлен степени 
|
| д) |  , где , где  – многочлен степени – многочлен степени 
|
| 14. | Для представления подынтегральной рациональной дроби в виде простейших дробей необходимо: а) найти корни знаменателя; б) установить, является ли дробь правильной; в) разложить знаменатель на множители. Укажите правильную последовательность действий. |
| 15. | Какой тип имеет простейшая подынтегральная дробь, если у нее  является корнем знаменателя кратности является корнем знаменателя кратности  , , 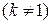 ? ?
|
| 16. | Для вычисления интеграла  необходимо сделать подстановку необходимо сделать подстановку  . Чему должно быть равно . Чему должно быть равно  ? ?
|
| 17. | Какими формулами определяется универсальная тригонометрическая подстановка? |
| 18. | Какой вид имеет подынтегральная функция при использовании тригонометрической подстановки  ? ?
|
| Неопределенный интеграл. Практические задания | |
| 19. | Чему равна производная от интеграла  ? ?
|
| 20. | График какой первообразной функции  проходит через точку с координатами проходит через точку с координатами  ? ?
|
| 21. | Укажите правильный ответ при вычислении интеграла  . .
|
| 22. | Какие табличные интегралы используются при вычислении интеграла 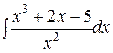 ? ?
|
| а) | 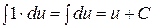
|
| б) |  
|
| в) | 
|
| г) | 
|
| д) | 
|
| 23. | Какие табличные интегралы используются при вычислении интеграла  ? ?
|
| 24. | Какие табличные интегралы используются при вычислении интеграла  ? ?
|
| 25. | Какие табличные интегралы используются при вычислении интеграла  ? ?
|
| 26. | Укажите, при помощи каких табличных интегралов вычисляют интеграл 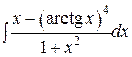 . Для этого используйте метод введения под знак дифференциала. . Для этого используйте метод введения под знак дифференциала.
|
| 27. | Укажите, при помощи каких табличных интегралов вычисляют интеграл  . Для этого используйте метод введения под знак дифференциала. . Для этого используйте метод введения под знак дифференциала.
|
| 28. | Укажите, при помощи каких табличных интегралов вычисляют интеграл 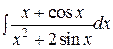 . Для этого используйте метод введения под знак дифференциала. . Для этого используйте метод введения под знак дифференциала.
|
| 29. | Укажите, при помощи каких табличных интегралов вычисляют интеграл  . Для этого используйте метод введения под знак дифференциала. . Для этого используйте метод введения под знак дифференциала.
|
| 30. | Укажите, при помощи каких табличных интегралов вычисляют интеграл  . Для этого используйте метод введения под знак дифференциала. . Для этого используйте метод введения под знак дифференциала.
|
| 31. | Укажите, при помощи каких табличных интегралов вычисляют интеграл 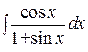 . Для этого используйте метод введения под знак дифференциала. . Для этого используйте метод введения под знак дифференциала.
|
| 32. | Укажите, при вычислении каких приведенных интегралов целесообразно сделать универсальную тригонометрическую подстановку  ? ?
|
| 33. | Что при вычислении интеграла  с помощью формулы интегрирования по частям выбирают за с помощью формулы интегрирования по частям выбирают за  , а что за , а что за  ? ?
|
| 34. | Каким образом в интеграле  необходимо разложить подынтегральную дробь на простейшие дроби? необходимо разложить подынтегральную дробь на простейшие дроби?
|
| 35. | Определить, как разложить подынтегральную дробь при вычислении интеграла  ? ?
|
| 36. | Какая подстановка рационализирует интеграл  ? ?
|
| 37. | Какая подстановка рационализирует интеграл  ? ?
|
|
|
|
|
|
|
| Определенный интеграл. Теоретические вопросы | |
| 38. | Какими линиями ограничена фигура, называемая криволинейной трапецией? |
| 39. | В каком из приведенных свойств определенного интеграла допущена ошибка? |
| а) | 
|
| б) | Если  , то , то  . .
|
| в) | 
|
| г) | 
|
| д) | 
|
| 40. | Какими линиями ограничена фигура, называемая криволинейным сектором? |
| 41. | Каким условиям должны удовлетворять функции  и и  , чтобы была справедлива формула Ньютона-Лейбница , чтобы была справедлива формула Ньютона-Лейбница  ? ?
|
| 42. | Чему равняется  ? ?
|
| 43. | Чему равняется  ? ?
|
| 44. | Какому условию должна удовлетворять подынтегральная функция  , чтобы выполнялось равенство , чтобы выполнялось равенство  ? ?
|
| 45. | Какому условию должна удовлетворять подынтегральная функция  , чтобы выполнялось равенство , чтобы выполнялось равенство  ? ?
|
| 46. | Какой вид имеет формула интегрирования по частям в определенном интеграле? |
| 47. | Укажите, в каких из приведенных интегралов необходимо применить формулу интегрирования по частям? |
| а) |  , где , где  – многочлен степени – многочлен степени 
|
| б) | 
|
| в) |  , где , где  – многочлен степени – многочлен степени 
|
| г) | 
|
| д) | 
|
| 48. | Какая формула используется при вычислении площади кривой 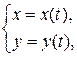  , ограниченной прямыми , ограниченной прямыми   и осью и осью  ? ?
|
| 49. | Какая формула используется для вычисления площади фигуры, заданной условиями  , ,  ? ?
|
| 50. | Какая формула используется для вычисления длины дуги кривой  ? ?
|
| 51. | Какая формула используется для вычисления длины дуги кривой, заданной в полярных координатах |
|
|
|
Воспользуйтесь поиском по сайту:

©2015 - 2026 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...

