Выбор настроек системы регулирования

Для полученной в [2] системы регулирования, время переходного процесса будет определяться значениями коэффициентов  и  регулятора . Так как заданная длительность переходного процесса достаточно мала, необходима очень точная настройка регулятора. Для настройки регулятора воспользуемся алгоритмом симплекс поиска.

Начальные условия для симплекс поиска:

; ;         ;

Результатом симплекс поиска оказалась точка:

; ; ;

Реакция системы на единичное входное воздействие при данных настройках регулятора приведена на рис. 1. Реакция системы на единичное неконтролируемое возмущающее воздействие приведена на рис. 2. Реакция системы на единичное контролируемое возмущение приведена на рис. 3.

4. Исследование устойчивости системы

Для построения областей устойчивости воспользуемся условием, данным в пункте 5 рекомендаций к курсовой работе:

,

где  - достаточно большая величина на порядок превышающая величину выходной переменной. Принимаем .

Область устойчивости системы на плоскости коэффициентов  регулятора  приведена на рис. 4.

Области устойчивости системы на плоскостях , ,  приведены на рис. 5, 6 и 7 соответственно.

 

 

       "Неровность" границы областей устойчивости связана с тем, что на интервале моделирования модуль ошибки регулирования расходящегося процесса "не успел" превысить заданную величину. На рис. 8 отображена область устойчивости на плоскости  регулятора . Цвет характеризует время переходного процесса (чем ярче точка, тем короче переходный процесс), заштрихованная область – это область, в которой переходный процесс не завершился на интервале моделирования и модуль величины ошибки

не превысил максимального значения.

По рис. 8 можно определить направление расширения области (в сторону "гребней"), в которой, при увеличении интервала моделирования, переходный процесс успеет завершится. Во всех остальных областях устойчивости наблюдается аналогичная картина – лучеобразное расширение области при увеличении интервала моделирования (например, рис. 9 – область устойчивости (T/T_м; t/t_м)).

5. Исследование чувствительности системы

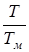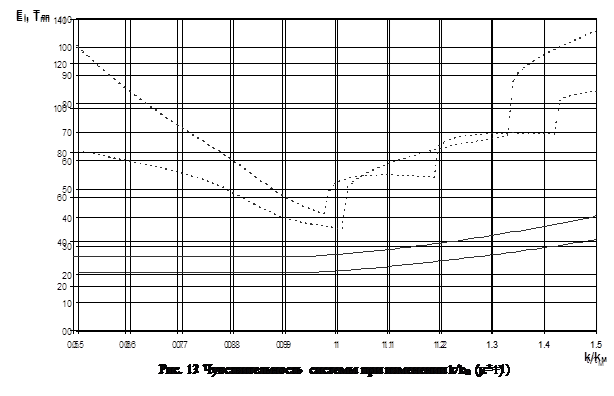
Для исследования чувствительности системы варьируются параметры ; ;  на интервале ±50% от номинальной величины при единичном задающем воздействии (рис. 10, 11 и 12) и единичном неконтролируемом возмущении (рис. 13, 14 и 15). Показателем чувствительности были выбраны интегральная ошибка системы (сплошная линия) и время регулирования (штрихпунктирная линия).

 

 

Вывод

Исследование чувствительности системы показало, что увеличение отношения  при единичном задающем воздействии вызовет резкий скачек времени регулирования, связанный с колебательностью переходного процесса, и незначительно уменьшит интегральную ошибку системы. По этой же причине произойдет скачек времени регулирования при изменении отношения  и , но интегральная ошибка увеличится. Уменьшение данных отношений вызовет плавное увеличение времени регулирования.

При единичном возмущающем воздействии уменьшение отношений (приблизительно на 0.95) вызовет резкий спад времени регулирования и последующее его плавное увеличение. При увеличении отношений  и  будет увеличиваться интегральная ошибка системы и, скачкообразно, время регулирования. Для 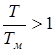 время регулирования будет увеличиваться плавно.

В обоих случаях, при вариации коэффициентов, интегральная ошибка системы не изменяется более чем на 45%.

Список литературы

1. Ротач В. Я. Расчет динамики промышленных автоматических систем регулирования. – М.: Энергия, 1973. -440с.

 

2. Анализ и синтез систем автоматического регулирования: Метод. указ. Сост.:
Ю. Н. Марченко: НФИКемГУ. – Новокузнецк, 2001. – 14 с.

12	Поделиться:

Воспользуйтесь поиском по сайту: