Расчет большинства конкретных статистических показателей основан на использовании средней агрегатной, средней арифметической или средней гармонической.

Все средние, за исключением средней агрегатной, могут рас­считываться в двух вариантах - как взвешенные или невзвешен­ные.

Пример. По данным табл. 6.3 рассчитаем среднюю заработную плату в целом по трем предприятиям АО.

Определим исходное соотношение средней для показателя «Средняя заработная плата».

Таблица 6.3

 

ЗАРАБОТНАЯ ПЛАТА ПРЕДПРИЯТИЙ АО

Предприя­тие	Численность промышленно-произ-водственного пер­сонала, чел.	Месячный фонд заработной платы, тыс. руб.	Средняя заработная плата, руб.
А
		564,84 332,75 517,54
Итого		1415,13	?

Независимо от имеющихся в на­шем распоряжений данных средняя заработная плата может быть получена только через следующее отношение:

 

 

Предположим, что мы располагаем только данными гр. 1 и 2 табл. 6.3. Итоги этих граф содержат необходимые величины для расчета искомой средней. Воспользуемся формулой средней агрегатной:

руб.,

где

x_i - i-й вариант осредняемого признака;

f_i - вес i-го варианта.

Если мы располагаем только данными о средней заработной плате и численности работников (гр. 1 и 3), то нам известен знаменатель исходного соотношения, но не известен его числитель. Однако фонд заработной платы можно получить умножением средней заработной платы на численность ППП. Поэтому общая средняя может быть рассчитана по формуле средней арифметической взвешенной:

руб.

Необходимо учитывать, что вес (f) в отдельных случаях может представлять собой произведение двух или даже трех значе­ний.

В статистической практике находит применение и средняя арифметическая невзвешенная: , где n - объем совокупности.

Эта средняя используется тогда, когда веса (f) отсутствуют: (каждый вариант признака встречается только один раз) или равны между собой.

Допустим теперь, что в нашем распоряжении только данные о фонде заработной платы и средней заработной плате персонала (гр. 2 и 3 табл. 6.3), т. е. нам известен числитель исходного соотношения, но не известен его знаменатель. Численность работников по каждому предприятию можно получить делением фонда заработной платы на среднюю заработную плату. Тогда расчет средней заработной платы в целом по трем предприятиям,

будет произведен по формуле средней гармонической взвешен­ной:

руб.

Средние показатели могут рассчитываться по дискретным и интервальным вариационным рядам. При этом расчет произво­дится по средней арифметической взвешенной. Для дискретного, ряда данная формула используется так же, как и в приведенном выше примере. В интервальном же ряду для расчета определя­ются середины интервалов.

Пример. Рассмотрим табл. 6.4.

Определим величину среднедушевого денежного дохода в целом по Российской Федерации. Исходное соотношение такой средней будет иметь следующий вид:

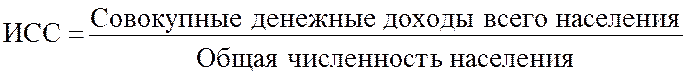
Перейдем от интервалов к их серединам. При этом величину первого интервала условно приравняем к величине второго, тог­да его нижняя граница будет равна 20 тыс. руб. Величину последнего интервала условно приравняем к величине предпослед­него, тогда его верхняя граница составит 240 тыс. руб. В результате "получаем следующие середины интервалов:

30 50 70 90 110 140 180 220.

 

Та б л и ц а 6.4

Распределение населения РФ в I квартале 2011 г.

По уровню среднедушевых денежных доходов

Среднедушевой денежный доход в среднем за месяц, тыс. руб.	Численность населения, % к итогу
До 40 40 - 60 60 - 80 80 - 100 100 - 120 120 - 160 160- 200 200 и выше	30,2 24,4 16,7 10,5 6,5 6,7 2,7 2,3
Итого

Роль численности населения в данном случае выполняет его доля в общем итоге, выраженная в процентах. Для расчета вос­пользуемся средней арифметической взвешенной:

тыс. руб.

Следовательно, Среднедушевой денежный доход в целом по Российской Федерации составлял 68,85 тыс. руб.

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: