 |
3. Постановка задачи. 4. Порядок выполнения работы. 5. Содержание отчета. Лабораторная работа № 6. Сортировка элементов массива
|
|
|
|
3. Постановка задачи
Создать объекты класса < имя класса> (класс и его поля задаются в соответствии с выбранным вариантом в лабораторной работе 1), причем объекты класса должны хранить данных о предметной области, связанные со свойствами предмета задания по варианту. Сохранить данные объекты в файле. Причем сохранить необходимо как отдельные объекты, так объект контейнерного типа, полученный в лабораторной работе 4. Считать сохраненные данные из файла и вывести их на экран.
4. Порядок выполнения работы
В главном меню системы программирования выберите команду File New Project или щелкните на соответствующей инструментальной кнопке. В окне New Project выберите пункт Console Application и щелкните на кнопке OK. В открывшемся окне в соответствии с вариантом задания напишите программу сохранения в файл и чтения из файла данных, использующую созданные вами объекты.
5. Содержание отчета
5. 1 Тема и цель работы.
5. 2 Текст программы.
5. 3 Результаты выполнения программы.
Лабораторная работа № 6
Сортировка элементов массива
1. Цель работы. Ознакомиться с различными методами сортировки массивов.
2. Общие сведения
Сортировка – это процесс перегруппировки заданного множества объектов в некотором определённом порядке. Целью сортировки является облегчение поиска элементов в массиве.
Существует множество методов сортировки, каждый из которых имеет свои достоинства и недостатки. Выбор алгоритма зависит от структуры обрабатываемых данных.
Методы сортировки можно разбить на два класса – сортировку массивов и сортировку файлов. Иногда их называют внутренней и внешней сортировкой, так как массивы хранятся в быстрой, оперативной, внутренней памяти машины со случайным доступом, а файлы размещаются в более медленной, но и более ёмкой внешней памяти.
|
|
|
Основным условием выбора метода сортировки должно являться экономное использование доступной памяти. Это предполагает, что перестановки, приводящие элементы в порядок, должны выполняться «на том же месте», т. е. методы, в которых элементы из массива «А» передаются в массив «В», представляют существенно меньший интерес. Поэтому будем классифицировать методы по их экономичности, т. е. по времени их работы. Хорошей мерой эффективности может быть С – число необходимых сравнений и М – число перестановок элементов. Эти числа есть функции от n – числа сортируемых элементов.
Сортировка массива методом прямого выбора
Алгоритм сортировки массива по возрастанию методом прямого выбора может быть представлен так:
1. Просматривая массив от первого элемента, найти минимальный элемент и поместить его на место первого элемента, а первый – на место минимального.
2. Просматривая массив от второго элемента, найти минимальный элемент и поместить его на место второго элемента, а второй – на место минимального.
3. И так далее до предпоследнего элемента.
Таблица 1 – Пример сортировки с помощью прямого выбора
Сортировка массива методом прямого обмена (пузырьковым методом)
В основе алгоритма метода прямого обмена лежит обмен соседних элементов массива. Каждый элемент массива, начиная с первого, сравнивается со следующим, и если он больше следующего, то элементы меняются местами. Таким образом, элементы с меньшим значением продвигаются к началу массива (всплывают), а элементы с большим значением – к концу массива (тонут), поэтому этот метод иногда называют " пузырьковым". Этот процесс повторяется на единицу меньше раз, чем элементов в массиве.
|
|
|
Сортировка массива методом прямого включения
Сортировка методом прямого включения, так же, как и сортировка методом простого выбора, обычно применяется для массивов, не содержащих повторяющихся элементов.
Сортировка этим методом производится последовательно шаг за шагом. На k–м шаге считается, что часть массива, содержащая первые k–1 элемент, уже упорядочена, то есть 
.
Далее необходимо взять k–й элемент и подобрать для него место в отсортированной части массива такое, чтобы после его вставки упорядоченность не нарушилась, то есть надо найти такое 
что 
. Затем надо вставить элемент a(k) на найденное место.
С каждым шагом отсортированная часть массива увеличивается. Для выполнения полной сортировки потребуется выполнить n–1 шаг.
Осталось ответить на вопрос, как осуществить поиск подходящего места для элемента х. Поступим следующим образом: будем просматривать элементы, расположенные левее х (то есть те, которые уже упорядочены), двигаясь к началу массива. Нужно просматривать элементы а(j), j изменяется от k–l до 1. Такой просмотр закончится при выполнении одного из следующих условий:
• найден элемент 
, что говорит о необходимости вставки х между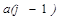 
и а(j).
• достигнут левый конец упорядоченной части массива, следовательно, нужно вставить х на первое место.
До тех пор, пока одно из этих условий не выполнится, будем смещать просматриваемые элементы на 1 позицию вправо, в результате чего в отсортированной части будет освобождено место под х.
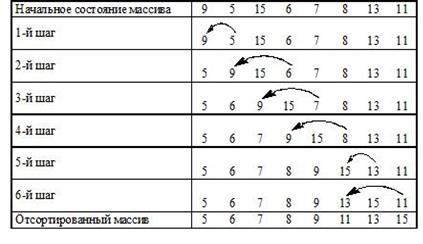
Методику сортировки иллюстрирует таблица 2.
Первоначально упорядоченная последовательность состоит из 1–го элемента 9. Элемент а(2)=5 – первый из неупорядоченной последовательности и 5 < 9, поэтому ставится на его место, а 9 сдвигается вправо. Теперь упорядоченная последовательность состоит из двух элементов 5, 9. Элемент а(3)=15 неупорядоченной последовательности больше всех элементов упорядоченной последовательности, поэтому остаётся на своём месте и на следующем шаге упорядоченная последовательность состоит из 5, 9, 15, а рассматриваемый элемент 6. Процесс происходит до тех пор, пока последовательность не станет упорядоченной.
Таблица 2 – Пример сортировки с помощью прямого включения
|
|
|
Шейкерная сортировка
Метод пузырька допускает три простых усовершенствования. Во-первых, если на некотором шаге не было произведено ни одного обмена, то выполнение алгоритма можно прекращать. Во-вторых, можно запоминать наименьшее значение индекса массива, для которого на текущем шаге выполнялись перестановки. Очевидно, что верхняя часть массива до элемента с этим индексом уже отсортирована, и на следующем шаге можно прекращать сравнения значений соседних элементов при достижении такого значения индекса. В-третьих, метод пузырька работает неравноправно для " легких" и " тяжелых" значений. Легкое значение попадает на нужное место за один шаг, а тяжелое на каждом шаге опускается по направлению к нужному месту на одну позицию.
На этих наблюдениях основан метод шейкерной сортировки (ShakerSort). При его применении на каждом следующем шаге меняется направление последовательного просмотра. В результате на одном шаге " всплывает" очередной наиболее легкий элемент, а на другом " тонет" очередной самый тяжелый. Пример шейкерной сортировки приведен в таблице 3.
Таблица 3 – Пример шейкерной сортировки
Шейкерную сортировку рекомендуется использовать в тех случаях, когда известно, что массив " почти упорядочен".
Сортировка массива с помощью включений с уменьшающимися расстояниями (метод Шелла)
Д. Шеллом было предложено усовершенствование сортировки с помощью прямого включения.
Идея метода: Сначала отдельно группируются и сортируются элементы, отстоящие друг от друга на расстоянии 4. Такой процесс называется четверной сортировкой. В нашем примере восемь элементов и каждая группа состоит точно из двух элементов. После первого прохода элементы перегруппировываются – теперь каждый элемент группы отстоит от другого на две позиции – и вновь сортируются. Это называется двойной сортировкой. И, наконец, на третьем проходе идет обычная, или одинарная, сортировка.
На первый взгляд можно засомневаться: если необходимо несколько процессов сортировки, причем в каждый включаются все элементы, то не добавят ли они больше работы, чем сэкономят? Однако на каждом этапе либо сортируется относительно мало элементов, либо элементы уже довольно хорошо упорядочены, и требуется сравнительно немного перестановок.
|
|
|
Ясно, что такой метод в результате дает упорядоченный массив, и, конечно же, сразу видно, что каждый проход от предыдущих только выигрывает (так как каждая i-сортировка объединяет две группы, уже отсортированные 2i-сортировкой). Также очевидно, что расстояния в группах можно уменьшать по-разному, лишь бы последнее было единичным, ведь в самом плохом случае последний проход и сделает всю работу. Однако совсем не очевидно, что такой прием " уменьшающихся расстояний" может дать лучшие результаты, если расстояния не будут степенями двойки.
Пример сортировки методом Шелла приведен в таблице 4.
Анализ этого алгоритма поставил несколько весьма трудных математических проблем, многие из вторых так еще и не решены. В частности, неизвестно, какие расстояния дают наилучшие результаты. В работе «Искусство программирования» Кнут показывает, что имеет смысл использовать такую последовательность (она записана в обратном порядке): 1, 4, 13, 40, 121, … или 1, 3, 7, 15, 31,.... Математический анализ показывает, что в последнем случае для сортировки п элементов методом Шелла затраты пропорциональны 
. Хотя это число значительно лучше п2, тем не менее мы не ориентируемся в дальнейшем на этот метод, поскольку существуют алгоритмы еще лучше.
Таблица 4 – Пример сортировки методом Шелла
|
|
|
