Связь с линейными операторами.

Перемещения

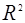Пусть X - множество всех точек прямой , плоскости  или трехмерного пространства 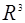. Обозначим через d(P, Q)  расстояние между точками P и Q множества X. Отображение f: X ® X f(P) = P называется перемещением, если для всех P и Q  d(P, Q) = d(P, Q).

     Примеры.

1. Пусть в 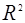 выбрана правая декартова прямоугольная система координат (x, y) с началом О. Поворот  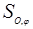плоскости на угол j вокруг точки О задается формулами R = 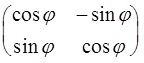R. Здесь 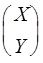R =  , R = 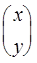. Очевидно, поворот является перемещением плоскости.

Отметим, что 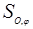(О) =О, то есть точка О остается неподвижной при повороте. Аналогично, в  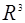можно рассмотреть поворот 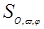на угол j вокруг оси, заданной единичным вектором v и точкой О. Легко проверить, что это перемещение задается формулой: R = R cosj + (R ´ v)sinj + v (1-cosj)(R × v). Все точки оси поворота являются неподвижными.

2. Перемещением будет и параллельный перенос 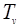 на вектор v, Очевидно,

R = R + v. Неподвижных точек перенос не имеет.

3. Пусть l некоторая прямая в 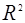. (Зеркальное) отражение  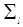относительно этой прямой является перемещением. Если в декартовой прямоугольной системе координат уравнение прямой имеет вид y = tg(j/2) x, то отражение задается формулой: R = 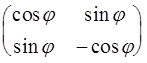R. Аналогично, если p некоторая плоскость в 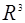, то отражение  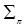относительно этой плоскости будет перемещением. Если n единичный вектор нормали к плоскости p, проходящей через начало координат, то R = R - 2(R × n) n.

Переносы и отражения (примеры 2 и 3) можно рассматривать и в .

4. Композиция U*V (последовательное выполнение) двух перемещений U и V      снова будет перемещением: (U*V)(P) = U(V(P)). Например, 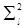 = 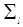*  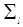= I - тождественное перемещение.

 

Связь с линейными операторами.

Теорема 1

Пусть f: X ® X - перемещение, A, B, C, D - точки X, f(A) = A и т.д. Если AB = CD (как свободные векторы), то A B = C D.

Доказательство.

Достаточно проверить, что в условиях теоремы четырехугольник ABDC является параллелограммом. Пусть О точка пересечения диагоналей AD и BC. Принадлежность точки О отрезку АD равносильно равенству: d(A, O) + d(O, D) = d(A, D). Поскольку для образов этих точек имеет место аналогичное равенство d(A, O) + d(O, D) = d(A, D), мы видим, что O лежит на отрезке AD и делит его пополам, поскольку d(A, O) = d(A,O) = 1/2 d(A,D) = 1/2 d(A, D). Аналогично, O лежит на CD и делит его пополам. Следовательно, ABDC - параллелограмм.

Из теоремы 1 следует, что если 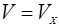 - пространство свободных векторов, то для всякого перемещения f: X ® X определено отображение: f*: V ® V.

Отметим, что если О - некоторая фиксированная точка X, то для любой точки P точка f(P) получается из O переносом на вектор f*(OP). Отсюда вытекает, что перемещение f однозначно определяется отображением f* и точкой O.

Теорема 2.

Отображение f* является линейным оператором в V и сохраняет скалярное произведение.

Доказательство.

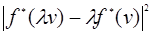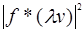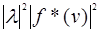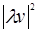Свойство f*(u + v) = f*(u) +f*(v) следует из определения сложения векторов: если u = AB, v = BC, то u + v = AC. Так как при перемещении любой треугольник ABC переходит в равный треугольник, то сохраняются не только длины, но и углы между векторами, а значит и скалярное произведение. Наконец, использую сохранение скалярного произведения, имеем: = -2 +  = - 2 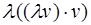+ 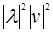=0. Следовательно, f*(l v) = lf*(v), то есть отображение f* линейно.

Следствие

Отображение 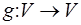 евклидова пространства V, обладающее свойством  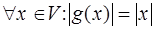является линейным оператором и сохраняет скалярное произведение.

Как известно, оператор в конечномерном пространстве определяется своей матрицей. Матрица A оператора, сохраняющего скалярное произведение, называется ортогональной и имеет следующие свойства:

1. Матрица А невырождена, более того det(A) = 1. Операторы с определителем 1 сохраняют ориентацию пространства, а с определителем (-1) меняют ее на противоположную.

2. Все собственные значения A - комплексные числа по модулю равные 1.

Кроме того, известны простейшие формы ортогональных матриц в ортонормированном правом базисе. Эти простейшие формы указаны в следующей таблице:

 

dimV	det(A) = 1	Название	det(A) = -1	Название
1	I  = (1)	Тождест-венный оператор	s = (-1)	Отраже-ние
2	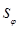=	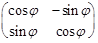Поворот на угол j	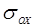=	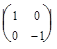Отраже-ние
3	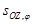=	Поворот на угол j вокруг OZ	=	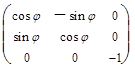Зеркаль-ный пово-рот

 

Замечание 1.

Учитывая связь между перемещением f и оператором f*, можно утверждать, что в подходящей декартовой системе координат имеет место формула:

R = АR + v, где А - одна из матриц из таблицы,   а v - некоторый вектор. Следовательно, всякое перемещение f имеет обратное , которое задается формулой R = 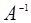(R - v) = 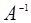R - 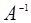v. Поскольку матрица  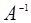- ортогональна, обратное отображение также является перемещением. Отметим еще, что для всякой ортогональной матрицы P и любого вектора w  преобразование R = PR + w является перемещением.

Замечание 2.

Имеется существенное различие между математическим понятием перемещения и физическим понятием движения. Во втором случае имеется в виду непрерывное во времени изменение положения точки, в то время как в первом фиксируются только ее начальное и конечное положения.

Перемещения с det(A) = 1 можно представлять себе и как движения, в то время как при det(A)= -1 такое представление невозможно, если оставаться в пределах исходного пространства X.  

 

12	Поделиться:

Воспользуйтесь поиском по сайту: