Принципы построения сетевых графиков.

ТЕМА МОДЕЛИ СЕТЕВОГО ПЛАНИРОВАНИЯ

1 Основные принципы построения сетевой модели

2 Расчет сетевой модели

3 Построение календарных графиков комплекса взаимоувязанных работ и расчет потребности в рабочей силе

 

1 Основные принципы построения сетевой модели

Сетевые методы — совокупность математических методов, в основе которых лежит графиче­ское представление комплекса работ в виде сетевого графика (сети).

 

Графическое изображение сете­вой модели называется сетевым графиком.(рис 1).

 

 

Рисунок 1 – Сетевой график

 

 

Сетевой график представляет собой ориентированный граф без петель и контуров. Обозначим его G =(Е, 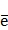 ), где Е—непустое конечное множество вершин, а  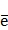— конечное множество ориентированных дуг, соединяющих некоторые пары вершин.

 

 

Дугам на сетевом графике соответствуют работы, а вершинам — события

 

Работа — это любые действия, трудовые процессы, сопровождающиеся затратами времени или (и) ресурсов и приводящие к определенным результатам.

 

Все работы можно подразделить на действительные работы, ожидания, фиктивные работы (зависимости).

Под действительными работами следует понимать любой трудовой процесс, тре­бующий ресурсов и имеющий некоторую продолжительность.

 

Ожидание — некоторый процесс, не требующий ресурсов, но имеющий некоторую продолжительность.

 

Фиктивные работы (зависимости) не требуют ресурсов и имеют нулевую продолжительность, они используются для обозначе­ния логических зависимостей между действительными работами.

 

Событие обозначает факт окончания работ, в него входящих, или начала работ, из него выхо­дящих, оно не имеет продолжительности и не потребляет ресурсов.

 

На любом сетевом графике можно выделить исходное, промежуточное и завершающее события.

Исходное событие указывает на факт начала выполнения всего комплекса работ, описывае­мого сетевой моделью.

Промежуточное событие пред­ставляет собой результат одной или нескольких работ, который обеспечивает возможность начать одну или несколько последующих работ.

Завершающее событие указывает на факт достижения цели, т.е. окончание всего комплекса работ. Оно не имеет последующих работ. Если завершающее событие одно, то сетевой график одноцелевой.

 

 

Любая работа сетевой модели соединяет два события: начальное и конечное. Для однозначного обозначения работ используют идентификаторы (i, j), где i — номер начального события работы, j — номер конечного события работы. Обычно на сетевых графиках события упорядочены, т.е. i <j.

 

Принципы построения сетевых графиков.

1. Как правило, последовательность работ изображается слева направо.

2. Работы А и В, выполняющиеся последовательно, изображаются следующим образом:

 

 

 

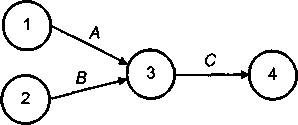
3 Если для выполнения работ А и В необходим результат работы С, то на сетевом графике они имеют вид

 

4 Если для выполнения работы С требуется результат работ А и В, то на сетевом графике они изображаются следующим образом:

5 Если работа С следует за двумя параллельно идущими работами А и В, а работа D только за работой В, то данные работы изображаются в следующей последовательности:

 

 

6 Одноцелевые графики имеют одно начальное и одно конечное события.

7 На сетевых графиках не должно быть тупиков, т.е. событий (кроме завершающего), из ко­торых не выходит ни одна работа.

8 Не должно быть событий (кроме исходного), которым не предшествует ни одна работа.

 

9 Не должно быть замкнутых циклов (контуров), т.е. путей, соединяющих некоторые события с ними же самими.

 

10 Два события не могут быть соединены более чем одной работой (петля). В этом случае ре­комендуется ввести дополнительное событие и фиктивную работу.

 

11 В сетевых моделях следует соблюдать определенную последовательность в нумерации со­бытий — от исходного к завершающему. События должны быть упорядочены по рангам, так как гра­фики с нумерацией событий по правилу i <j удобны для анализа и проведения расчетов.

 

Для упорядочения вершин можно воспользоваться графическим способом (методом вычеркивания дуг):

1. Исходную вершину (в которую не входит ни одна дуга) отнесем к рангу 0 и присвоим ей номер 1.

2. Вычеркнем все дуги, выходящие из вершины 1. События, оказавшиеся без входящих дуг, отнесем к первому рангу и присвоим им в произвольном порядке номера 2, 3, …, к1.

3. Вычеркнем все дуги, выходящие из вершин предыдущего ранга; отнесем вершины, оказав­шиеся без входящих дуг, к следующему рангу и последовательно пронумеруем их. Этот шаг повторя­ем до тех пор, пока все вершины не будут пронумерованы. В результате события оного и того же ранга между собой не соединены работами, а события старших рангов имеют больший номер. Поря­док нумерации событий одного и того же ранга может быть произвольным.

 

 

В случае необходимости упорядочения сетей большой размерности удобно пользоваться ана­литическим методом — алгоритмом Форда.

Прежде чем представлять комплекс работ сетевым графиком, необходимо составить перечень работ, подлежащих выполнению, оценить продолжительность каждой из них и установить последовательность выполнения работ. Такой перечень удобно представить в виде структурно-временной таблицы.

 

Пример 1. Университет рассматривает предложение о строительстве нового корпуса. Работы, которые следует выполнить перед началом строительства, представлены в табл.1.

Таблица1 – Исходные данные

Работа	Содержание работы	Предшествующие работы	Продолжительность работы, недель
А1	Определить место строительства	—	6
А2	Разработать первоначальный проект	A1	8
А3	Получить разрешение на строительство	А1	12
а4	Выбрать архитектурную мастерскую	А3	4
А5	Разработать смету затрат на строительство	А3	12
А6	Закончить разработку проекта	А2, А4, А5	10
A7	Получить финансовое обеспечение	А2, А5	12
A8	Нанять подрядчика	А6, А7	8

 

Требуется построить сетевой график проекта.

 

Решение.

 

Рис.  2. Сетевой график

 

 

2 Расчет сетевой модели

 

Для выполнения любой работы требуется некоторое время и ресурсы. Время, необходимое для выполнения работы (i,j), будем называть продолжительностью работы и обозначать t_ij.

 

 

Любая последовательность работ, в которой конечное событие предыдущей работы является начальным событием последующей, называется путем и обозначается L с перечислением всех собы­тий, входящих в данный путь (i1—i2—...—in)

 

Полный путь — последовательность работ, соединяющих исходное и завершающее события.

 

Путь, предшествующий событию, — последовательность работ, соединяющих исходное и рас­сматриваемое события.

 

Путь, следующий за событием, — последовательность работ, соединяющих рассматриваемое и завершающее события.

 

Под длиной пути будем понимать продолжительность выполнения всей последовательности работ, составляющих этот путь.

 

Критический путь — это наиболее протяженный по времени полный путь. Его продолжитель­ность определяет минимальное время выполнения всего проекта, которое называется критическим сроком и обозначается t_кр.

На сетевом графике критических путей может быть несколько. Работы и события, лежащие на критическом пути, называются критическими, а остальные работы и события — некритическими.

 

К основным временным параметрам сетевых графиков относятся:

• продолжительность критического пути (критический срок);

• сроки свершения и резервы событий;

• сроки выполнения отдельных работ и их резервы времени.

 

 

Ранний срок t_p(j) свершения события j — это самый ранний момент, к которому завершаются все работы, предшествующие этому событию:

 

t_p(1) = 0,

t_p(j)= max (tp(i) + t_ij) tϵU*

 

где U* — множество работ, входящих в j-е событие; t_р(i) — ранний срок свершения начального события работы (i, j); tij— продолжительность работы (i,j).

 

Тогда для завершающего события S t_р(S)= tкр

 

 Поздний срок t_n(i) свершения события i — такой предельный момент, после которого остается ровно столько времени, сколько необходимо для выполнения всех работ, следующих за этим событи­ем без нарушения сроков реализации проекта в целом.

 

Для завершающего события S предполагается, что

t_n(S) = t_р (S) = t_kp.

Тогда

t_n(i)= min(t_n(j)-tij),

Uj — множество работ, выходящих из i-го события; tn(j) — поздний срок свершения конечного события работы (i, j).

 

Резерв времени R(i) события i показывает, на какой предельно допустимый срок может задержаться свершение события i без нарушения срока наступления завершающего события:

Ранние и поздние сроки критических событий совпадают, т.е. резерв времени у них равен нулю.

 

Зная сроки свершения событий, можно найти ранние и поздние сроки начала и окончания работ.

· – ранний срок начала работы;

· – ранний срок окончания работы;

· – поздний срок окончания работы;

· – поздний срок начала работы;

· – полный резерв работы показывает максимальное время, на которое можно увеличить длительность работы 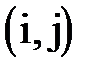 или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом;

· R₁(i, j) = t _п (j) – t _п (i) -   t (i, j) - частный резерв времени первого вида R₁(i,j) работы (i,j) есть часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока ее начального события.

· – частный резерв времени второго вида, или свободный резерв работы показывает максимальное время, на которое можно увеличить продолжительность работы 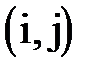 или отсрочить ее начало, не меняя ранних сроков начала последующих работ.

· R _н (i, j) = t _р (j) – t _п (i) -   t (i, j) - независимый резерв времени R _н работы (i, j) есть часть полного резерва времени, получаемая для случая, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие работы начинаются в ранние сроки

Критические работы, как и критические события, резервов времени не имеют.

Для упрощения расчетов воспользуемся четырехсекторной схемой. Кружок, изображающий событие, разобьем на 4 сектора, в каждом из которых запишем необходимую информацию (рис.3).

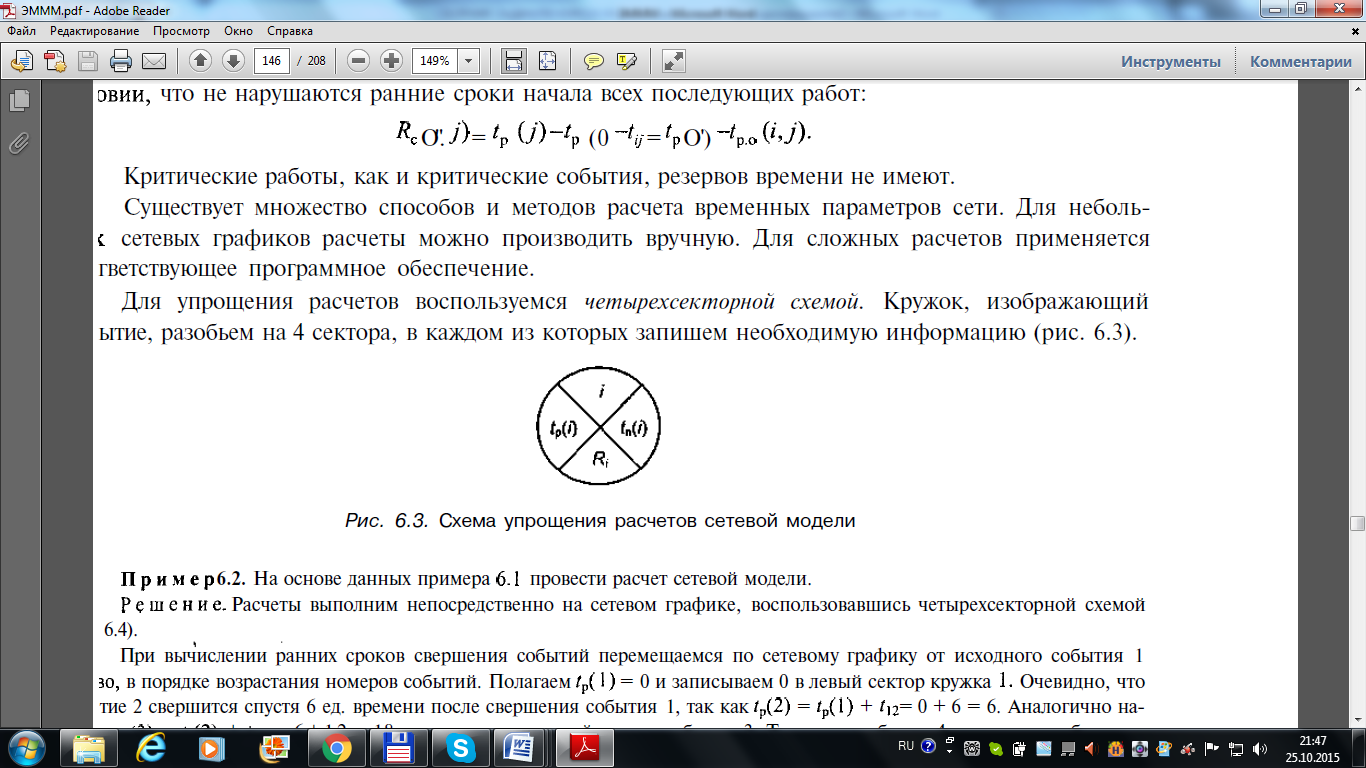
i	Ri
tp(i)	tn(i)

Рис.3. Отображение временных параметров событий на сетевом графике

 

 

Поделиться:

Воспользуйтесь поиском по сайту: