 |
Моделирование энергетических преобразований в системах формирования изображения
|
|
|
|
Модели машинной графики
Системы машинной графики отображают отработанную информацию о процессах или объектах в виде синтезированного отображения на экране дисплея или другой экранной плоскости. Для систем машинной графики источником входной информации является не сами физические процессы, а их математические модели. Такие модели в общем случае представляют упорядоченную совокупность данных, числовых характеристик, параметров, математических и логических зависимостей, отображающих структуру, свойства, взаимосвязи и отношения между элементами объекта, а также между объектом и его окружением.
Модели как правило являются обобщенными, предназначенными для описания класса объектов. Индивидуальный объект описывается вводом конкретных значений параметров системы.
Изображение, которому ставится в соответствие моделируемый аналог называется оригиналом.
При оценке степени соответствия синтезированного изображения и оригинала будем использовать три уровня подобия:
· физическое
· психофизическое (физиологическое)
· психологическое
· Физическое подобие устанавливается на уровне трех групп характеристик:
· геометрических (пространственных)
· яркостных (энергетических)
· временных
При физически точном подобии эти характеристики синтезированного изображения должны либо полностью соответствовать оригиналу, либо быть ему пропорциональными.
При психофизическом уровне подобия соответствие устанавливается на уровне зрительных ощущений. В силу ограниченных возможностей зрительного аппарата при некотором уровне искажений наблюдатель не ощущает разницу между синтезированным изображением и оригиналом.
|
|
|
Психологическое подобие предполагает, что по общему восприятию синтезированное изображение и оригинал являются схожими. В следствии этого синтезированное изображение обеспечивает формирование наблюдателя вполне определенного суждения о реальном или сюжете, хотя синтезированное изображение существенно отличается от оригинала по физическим характеристикам.
Пример
Задача, решаемая на уровне психологического подобия:
формирование трехмерных контурных изображений (чертежей), выполненных в выбранной аксонометрической проекции.
Необходимость синтеза изображения на уровне синтеза физического и психофизического подобия возникает при решении следующих задач:
имитация визуального наблюдения обстановки в видео-тренажерах
создание банков эталонных изображений автоматического распознавания систем
оценка внешнего вида и эстетических свойств проектируемых изделий или объектов.
В обобщенном виде процедуру синтеза изображения можно представить следующей формулой:
Gси=Aмг Gмод ,
где соответственно
Gмод - модель наблюдаемого объекта (сцены)
Aмг - оператор преобразования (обрабатываемая программа системы машинной графики)
Gси - двумерное изображение, сформированное системой
Синтезированное изображение сопоставляется с оригиналом при визуальной или аппаратурной съемке.
Gор=Gвиз=AвизGо
Gор=Gвых=AсGо,
где соответственно
Gо - поле излучения объекта,
Aвиз, Aс - соответственно операторы преобразования при визуальном наблюдении в съемочной аппаратуре,
Gвиз, Gвых - соответственно изображение, полученное при визуальном наблюдении или съемке,
Gор - изображение - оригинал.
При физическом уровне подобия оригинал и синтезированное изображение должны быть идентичны:
Gор Û Gси
Текстура изображения
Под текстурой понимают специфические изменения тона (цвета) в изображении объекта или некоторой его части.
|
|
|
К текстуре относятся также наличие характерных линий на изображении. Синонимами термина текстура являются узор, рисунок, фактура.
Виды текстуры
Упорядоченная. Изменение тона в виде правильных или почти правильных геометрических рисунков (кирпичная кладка, кафельная облицовка, шахматный рисунок).
Стохастическая (случайная). Присуща естественным объектам и как правило является следствием шероховатости поверхности.
Один из основных принципов формирования текстуры - перенос регулярного или стохастического рисунка на поверхность объекта.
Для нанесения рисунка решается задача преобразования систем координат. Если рисунок задан в пространстве текстуры в системе координат (U, W), а поверхность в (q,j), то для переноса рисунка определяется функция отображения одного пространства на другое, т.е. определяется соотношения:
q =f (U,W)
j =g (U,W)
U= n (q, j)
W=s (q, j)
В большинстве практических случаев такие преобразования линейны, а коэффициент преобразований может быть вычислен из соотношений между известными точками в системах координат. Характерные точки узора из пространства текстуры переносятся в объектное пространство. Затем в пространство изображений и определенным образом соединяются линии рисунка.
В процедурах нанесения узоров часто используются фрагментирование как узоров, так и поверхностей.
При переносе на поверхность предмета текстуры, представляющей непрерывное регулярное или случайное поле яркости наиболее подходящим является метод обратного трассирования лучей. Центр пикселя изображение проецируется на поверхность предмета и по координатам точки на поверхности определяется соответствующая ей точка в пространстве текстуры. Для устранения эффектов, вызванных пространственной дискретизацией используются процедуры сглаживания. Одной из возможных процедур сглаживания является трассирование четырех точек, соответствующим углам пикселя и использования среднего значения яркости текстуры для этих четырех точек. Использование четырех точек пикселя позволяет оценить достаточность процедуры сглаживания, если разность яркостей для выбранных четырех точек больше заданного порога, есть возможность произвести разбиение пикселя на четыре части и вычислить для него яркость более точно.
|
|
|
Для синтеза стохастических текстур предпочтительными считаются авто регрессионная модель и модели с использованием методов линейного программирования. Синтез осуществляется с использованием статистических характеристик текстур прототипов:
плотность вероятности
автокорреляционной функции.
Для определения плотности вероятности в пределах некоторого окна измеряют гистограмму, и для ее отображения используют первые четыре момента(среднее, стандартное отклонение, асимметрия, коэффициент эксцесса).
Форму автокорреляционной функции выражают через ее четыре центральных пространственных момента. В результате такой обработки формируется восьми мерный вектор признаков текстуры.
Примечание: стохастические текстуры, синтезированные на основе прототипов хорошо моделируют естественные шероховатые поверхности, если они обладают сравнительно не большой кривизной.
Для поверхностей со значительной кривизной (шар, эллипсоид), перенос на них даже стохастической текстуры не обеспечивает реалистического вида. Причина этого в том, что текстура, сформированная без учета формы объекта не передает изменение освещенности, обусловленной рельефом поверхности. Для реальных шероховатых поверхностей вектор нормали содержит небольшую случайную составляющую, которая определяет характер изменения освещенности в изображении. Для получения изображения, близкого к реалистичному этот фактор необходимо смоделировать.
N - нормаль к исходной поверхности определяется векторным произведением
N = Q ¢ u · Q ¢ w, где Q ¢ u, Q ¢ w - частные производные функции поверхности Q по направлениям U и W.
Нормаль N ¢ к возмущенной поверхности при малом возмущении F (U, W) вычисляется по формуле:
N ¢ = N+Fu (N Q ¢ w) / ï N ï + Fw (Q ¢ u N) / ï N ï,
где Fu, Fw - сечение функции F в данной точке по направлениям соответственно U и W.
В качестве функции F могут быть использованы как аналитические функции, так и заданные в виде массива. В частности в виде массива можно задать стохастическую текстуру.
|
|
|
Примечание: изображение при использовании данного метода отображения шероховатых поверхностей приобретает вид, чрезвычайно близкий к реалистичному, однако объем вычислений для алгоритма возмущения нормали примерно в 4-5 раз больше, чем при изображении текстуры без учета рельефа.
Аналогичные методы возмущения используют для придания естественного вида цветным поверхностям. К исходному цвету добавляется случайная или псевдослучайная составляющая другого цвета, точки поверхности приобретают цвет, являющийся интерполяцией между двумя крайними цветами. Метод применяется для моделирования поверхностей из гравия, цемента и т.д. Для моделирования наиболее сложных поверхностей, содержащих существенные нерегулярности (каменные осыпи, деревья, облака и т.д.) используются фронтальные поверхности, состоящие из случайно заданных полигональных или биполигональных фрагментов.
Моделирование энергетических преобразований в системах формирования изображения
Первое звено, осуществляющее преобразование лучистого потока от элементов сцены - это оптическая система, которая формирует первичное изображение на светочувствительной поверхности преобразователя.
Геометрические и энергетические характеристики первичного изображения, определяются на основе геометрической оптики, в соответствии с которой первичное изображение можно рассматривать как центральную проекцию наблюдаемой сцены на картинную плоскость.
Центральная проекция обеспечивает точное моделирование процессов геометрических и энергетических преобразований, но не позволяет передавать мелкую структуру изображения поскольку сам принцип центральной проекции не предусматривает учета дифракции, аберраций и прочих явлений, приводящих к размытию изображений.
При анализе энергетических преобразований и определения освещенности изображения в картинной плоскости полагаем, что расстояние от наблюдаемой сцены до объектива оптической системы много больше фокусного расстояния системы, а угловая ширина индикатрисы излучения любого участка наблюдаемых поверхностей существенно превышает угловой размер входного зрачка оптики из любой точки пространства предметов.
Для определения освещенности первичного изображения воспользуемся методами центральной проекции (рис.1).
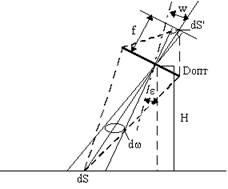
Рис.1 Геометрическая схема для определения освещенности первичного изображения
Элементу dS на поверхности наблюдения соответствует элемент dS¢ в картинной плоскости. Так как проективное преобразование оптической системы является центральным, то угол dw, опирающийся на площадку dS, равен углу dw¢ в пространстве изображений. Отсюда следует
|
|
|
dS cos e¢ /(H2/cos2 e¢) = dS¢ cos w/(f2/cos2w) (*)
Лучистый поток, собираемый системой от элемента dS, составляет
dФ = L dS cos e¢ dW tосtср (**)
где dW - телесный угол, образуемый косинусом лучей, поступающих от точки объекта в оптическую систему;
tос= k(w) tопт - коэффициент ослабления излучения оптической системы, равный произведению коэффициента виньетирования k(w) и коэффициента пропускания оптики tопт
tср - пропускание слоя среды между объектом и оптической системой
Учитывая, что dW = Sопт cos w/(H2/cos2 e¢)=pD2опт cos w cos2 e¢/(4 H2), получаем
dФ = pD2опт L cos w cos3 e¢ k(w) tосtсрdS/(4H2) (***)
Величина освещенности в плоскости первичного изображения определяется следующим образом: Eиз = dФ/dS¢=pD2опт L cos w cos3 e¢ k(w) tосtср dS/(4H2 dS¢)
Т.к. согласно (*) dS/dS¢= cos3w cos-3 e¢(H/f)2, то окончательно получаем
Eиз = p/4 (Dопт/f)2 L k(w) tопт tср cos4w (****)
Описание геометрических форм
Описание поверхностей
Параметрическое описание поверхностей
Поверхности, заданные в форме
Х = Х(u,t) где u,t - параметры, изменяющиеся в
Y = Y(u,t) заданных пределах,
Z = Z(u,t),
относятся к классу параметрических. Для одной пары значений (u,t) вычисляется одна точка поверхности.
|
|
|


