 |
Математические и алгоритмические основы решения задачи
|
|
|
|
Постановка задачи
Под надежностью понимают свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, хранения и транспортирования;
Надежность является комплексным свойством, которое в зависимости от назначения объекта может включать безотказность, ремонтопригодность и долговечность или сочетание этих свойств. Термин Надежность используется только для описаний общего характера в неколичественном выражении.
Показатель надежности - количественная характеристика одного или нескольких свойств, составляющих надежность объекта.
Требуется реализовать расчет надежности функционирования систем.
Пример расчета надежности системы, собранной по основной схеме.
На рисунке 1a, представлена схема включения конденсаторной батареи (l2 = l3 =... l11 = 0,01 1/год, = 0,024 1/год). Конденсаторы выбраны так, что при выходе из строя любого из них батарея не выполняет своих функций, то есть с точки зрения надежности она отказывает.
Отказывает она также при перегорании предохранителя 1. Следовательно, мы сформулировали понятие отказа - при отказе любого из элементов система, состоящая из 11 элементов, отказывает. На рисунке 1б изображена расчетная схема надежности, где все элементы включены последовательно.
Интенсивность отказов конденсаторной батареи составит:
.
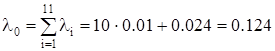Рисунок 1. Схема конденсаторной батареи
На рисунке 1в батарея представлена эквивалентным элементом с интенсивностью отказов lo. По отношению к более сложной системе (схеме), в которой составной частью является конденсаторная батарея, эта установка будет элементом с параметром lo.
|
|
|
Вероятность безотказной работы батареи за год равна:
.
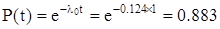Средняя наработка до отказа равна:
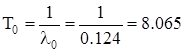года.
Результат расчета доказывает, что надежность неремонтируемой батареи конденсаторов, за 1 год непрерывной работы, мала. Для обеспечения более высокого уровня её надежности необходимо предусмотреть более качественное техническое обслуживание.
Рассмотрим случай, когда элементы включены параллельно.
Надежности участка логической схемы:
.
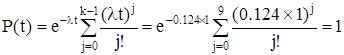Математические и алгоритмические основы решения задачи
Предположим, что система состоит из n последовательно включенных элементов. Из теории вероятностей известно, что если определены вероятности появления нескольких независимых случайных событий, то совпадение этих событий определяется как произведение вероятностей их появлений. В нашем случае работоспособное состояние любого из n элементов системы оценивается как вероятность безотказной работы элемента. Система будет находиться в работоспособном состоянии только при условии совпадения работоспособных состояний всех элементов. Таким образом, работоспособность системы оценивается как произведение вероятностей безотказной работы элементов:
, (2.1)
где 
- вероятность безотказной работы i-го элемента. Система, как и элемент, может находиться в одном из двух несовместимых состояний: отказа или работоспособности. Следовательно,
,
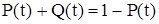где Q (t) - вероятность отказа системы, определяемая по выражению:
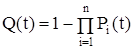. (2.2)
При произвольном законе распределения времени наработки до отказа для каждого из элементов:
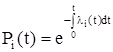, (2.3)
где 
- интенсивность отказов i-го элемента.
Вероятность безотказной работы системы соответственно запишется:
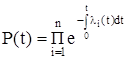. (2.4)
По выражению (2.4) можно определить вероятность безотказной работы системы до первого отказа при любом законе изменения интенсивности отказов каждого из n элементов во времени. Для наиболее часто применяемого условия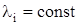 
выражение (2.4) примет вид:
|
|
|
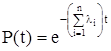, (2.5)
где 
можно представить как интенсивность отказов системы, сведенной к эквивалентному элементу с интенсивностью отказов:
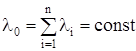. (2.6)
Таким образом, систему из n последовательно включенных элементов легко заменить эквивалентным элементом, который имеет экспоненциальный закон распределения вероятности безотказной работы. А это значит, если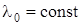 
, то средняя наработка до отказа системы
. (2.7)
Верно также и то, что при условии: 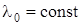, искомая величина определится как
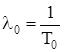. (2.8)
Для параллельного нагруженного логического соединения вероятность отказа системы равна произведению вероятностей отказа элементов. Функция ненадежности системы
, (2.9)
где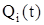 
- функция ненадежного j-го элемента.
При параллельном ненагруженном логическом соединении функция надежности участка логической схемы, состоящего из k одинаково надежных элементов, вычисляется по формуле:
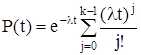(2.10)
Общий недостаток изложенного выше приближенного расчета надежности - малая и недостоверная информация о надежности типовых элементов.
Расчеты надежности при проектировании целесообразно завершить моделированием процессов появления отказов систем и испытанием первых опытных образцов. В ходе моделирования выявляются интенсивности отказов систем из-за постепенных изменений параметров элементов. При испытаниях уточняются действующие на элементы нагрузки и данные о надежности отдельных элементов.
|
|
|
