 |
СЧЁТЕСЛИ(интервал; критерий)
|
|
|
|
Интервал — диапазон, в котором нужно подсчитать ячейки.
Критерий — критерий в форме числа, выражения или текста, который определяет, какие ячейки надо подсчитывать в заданном интервале.
Например, критерий может быть записан следующим образом: 32, "32", ">32", "яблоки".
Пример: Пусть имеется таблица, содержащая информацию о сборе фруктов (Рис. 1):

Рис. 1
Тогда функция СЧЁТЕСЛИ(A3: С6;"яблоки") возвращает значение 2 (количество сборщиков яблок), а СЧЁТЕСЛИ(A3:C6;">55") возвращает значение 3 (количество сборщиков, собравших более 55 кг фруктов).
Точно такие же результаты дадут функции =СЧЁТЕСЛИ(B3:B6;"яблоки") и СЧЁТЕСЛИ(C3:C6;">55").
Обратите внимание на то, что условие, содержащее знаки операций отношений, должно заключаться в кавычки.
Функция СУММЕСЛИ()
Функция СУММЕСЛИ() действует аналогично функции СЧЕТЕСЛИ(), но вычисляет сумму содержимого ячеек заданного диапазона.
=СУММЕСЛИ(интервал выбора; критерий; интервал суммирования)
Интервал выбора — диапазон вычисляемых ячеек.
Критерий — критерий в форме числа, выражения или текста, определяющего суммируемые ячейки. Например, критерий может быть выражен как 32, "32", ">32", "яблоки".
Интервал суммирования — фактические ячейки для суммирования.
При выполнении этой функции суммируются значения только тех ячеек из интервала суммирования, для которых соответствующие значения в интервале выбора удовлетворяют критерию.
Например, для приведенной выше таблицы с данными о сборе фруктов по формуле
=СУММЕСЛИ(B3:B6;"яблоки";C3:C6) вычисляется вес всех собранных яблок.
Если аргумент интервал суммирования опущен, то суммируются значения ячеек из диапазона интервал выбора. Например, для той же таблицы значение функции СУММЕСЛИ(С3:С6;">50") равно 218.
|
|
|
Задания для самостоятельной работы:
Задание 1
Известны данные о мощности двигателя (в л. с.) и стоимости 20 легковых автомобилей. Определить общую стоимость автомобилей, у которых мощность двигателя превышает 100 л. с. Определить количество автомобилей стоимостью более 1.000.000 рублей.
Задание 2
Известна информация о багаже (количество вещей и общий вес багажа) 24 пассажиров. Определить суммарный вес багажа пассажиров, имеющих:
а) одну вещь;
б) более двух вещей.
Определить количество пассажиров, имеющих суммарный вес более 20 кг.
Задание 3
- Скопируйте таблицу 1 на новый лист.
| Таблица 1 | ||||||
| Фамилия | Имя | Отчество | Отдел | Оклад | Премия | Ставки |
| Андреева | Анна | Семеновна | Бухгалтерия | 0,2 | ||
| Бутаков | Андрей | Викторович | Сбыт | 0,15 | ||
| Горбатов | Иван | Андреевич | Склад | |||
| Ерохин | Иван | Олегович | Склад | |||
| Иванов | Сергей | Александрович | Бухгалтерия | |||
| Крылова | Ольга | Сергеевна | Кадров | |||
| Маметов | Иван | Алексеевич | Сбыт | |||
| Петрова | Мария | Павловна | Кадров | |||
| Чарушин | Семен | Максимович | Склад | |||
| Яровцева | Елена | Викторовна | Бухгалтерия | |||
| ИТОГО | ||||||
| Кол-во сотрудников | Суммы окладов | |||||
| Бухгалтерия | Бухгалтерия | |||||
| Сбыт | Сбыт | |||||
| Склад | Склад | |||||
| Кадров | Кадров | |||||
| ИТОГО | ||||||
| >6000 | ||||||
| Иван |
2. Отформатируйте таблицу согласно Рис. 2

Рис. 2
3. Определите общее количество сотрудников по каждому из отделов.
4. Подсчитайте количество сотрудников, имеющих оклад больше 6000 р.
|
|
|
5. Определите количество сотрудников с именем «Иван».
6. Подсчитайте общую сумму окладов сотрудников каждого отдела.
- Рассчитайте величину премии: для сотрудников, имеющих оклад меньше 5000 р., премия равна 20% от оклада, для остальных сотрудников – 15% от оклада.
Индивидуальные задания
1. 10 спортсменов принимают участие в соревнованиях по 5 видам спорта. По каждому виду спорта спортсмен набирает не более 100 очков. Определить среди 10 спортсменов участника с наибольшим суммарным количеством очков. Построить диаграмму, показывающую соотношение количества набранных очков, каждым спортсменом по каждому виду спорта.
2. 10 студентов сдают экзамены по 5 дисциплинам. По каждой дисциплине можно получить оценку – 2, 3, 4, 5. Определить среди 10 студентов человека с наибольшим средним баллом. Построить диаграмму, показывающую соотношение оценок, полученных каждым студентом по каждой дисциплине.
3. Для 10 человек по данным о ежемесячном доходе рассчитать подоходный налог 13%, единый социальный налог 5%. Округление произвести до копеек. Посчитать сумму к выдаче в рублях и $. Построить диаграмму, показывающую соотношение сумм уплаты налога по каждому виду налога.
4. Билет на пригородный поезд стоит 20 руб., если расстояние до станции не более 20 км; 50 руб., если расстояние до станции больше 20 км, но меньше 75 км; 100 руб., если расстояние больше 75 км. Составить таблицу со следующими столбцами: пункт назначения, расстояние, стоимость билета, количество проданных билетов до данного пункта назначения. Установить число станций в радиусе 50 км от города. Построить диаграмму, показывающую какая станция пользуется наибольшей популярностью по отношению к остальным.
5. Телефонная компания взимает плату за услуги телефонной связи по тарифу: 370 мин в месяц – абонентская плата 200 руб., за каждую минуту сверх нормы – 2 руб. Составить ведомость оплаты услуг телефонной связи для 10 абонентов за 1 месяц, самостоятельно указав количество потребляемого времени каждым. Построить диаграмму, показывающую сравнительную характеристику сумм оплаты услуг телефонной компании каждым абонентом.
6. Компания снабжает электроэнергией клиентов по тарифу:
|
|
|
5 руб. за 1 кВт/ч за первые 500 кВт/ч;
10 руб. за 1 кВт/ч свыше 500 кВт/ч, но не более 1000 кВт/ч;
15 руб. за 1 кВт/ч свыше 1000 кВт/ч.
Для 10 клиентов посчитать плату. Определить число клиентов, потребляющих более 1000 кВт/ч. Построить диаграмму, демонстрирующую сравнение потребляемой электроэнергии каждым клиентом.
7. Билет на пригородный поезд стоит 10 монет, если расстояние до станции не более 20 км; 15 монет, если расстояние до станции больше 20 км, но меньше 75 км; 25 монет, если расстояние больше 75 км. Составить таблицу со следующими столбцами: пункт назначения, расстояние, стоимость билета, количество проданных билетов до данного пункта назначения. Отсортировать таблицу по полю количество проданных билетов. Установить число станций в радиусе 60 км от города. Построить диаграмму, показывающую какая станция пользуется наименьшей популярностью по отношению к остальным.
8. Билет на пригородный поезд стоит 6 монет, если расстояние до станции не более 20 км; 10 монет, если расстояние до станции больше 20 км, но меньше 75 км; 15 монет, если расстояние больше 75 км. Составить таблицу со следующими столбцами: пункт назначения, расстояние, стоимость билета, количество проданных билетов до данного пункта назначения. Отсортировать таблицу по полю количество проданных билетов. Установить число станций в радиусе более 70 км от города. Построить диаграмму, показывающую, какая станция пользуется наименьшей популярностью по отношению к остальным.
9. 10 студентов сдают экзамены по 5 дисциплинам. По каждой дисциплине студент может получить оценку – 2, 3, 4, 5. Определить средний балл учащихся. Посчитать количество 5, 4, 3 и 2. Найти студента с наибольшим средним баллом и студента с наименьшим средним баллом. Построить диаграмму, показывающую соотношение оценок, полученных каждым слушателем по каждой дисциплине.
10. Для отдела из 10 человек составить ведомость расчета заработной платы. Таблица содержит следующие сведения: Ф.И.О., должность, оклад, стаж работы. Для каждого человека посчитать подоходный налог 13%, надбавку 5000 руб., если стаж работы более 3 лет и сумму к выдаче. Построить диаграмму, показывающую з/плату каждого сотрудника.
|
|
|
11. Для отдела из 10 человек составить ведомость расчета заработной платы. Таблица содержит следующие сведения: Ф.И.О., должность, оклад, стаж работы. Для каждого человека посчитать подоходный налог 13%, надбавку и сумму к выдаче. Надбавка составляет 10% от оклада, если стаж работы более 5 лет. Построить диаграмму, показывающую з/плату каждого сотрудника.
12. Компания снабжает электроэнергией клиентов по тарифу:
15 руб. за 1 кВт/ч за первые 500 кВт/ч;
20 руб. за 1 кВт/ч свыше 500 кВт/ч.
Для 10 клиентов посчитать плату. Определить число клиентов, потребляющих не более 500 кВт/ч и найти суммарное количество потребляемой энергии. Построить диаграмму, демонстрирующую сравнение потребляемой электроэнергии каждым клиентом.
13. Составьте экзаменационную ведомость, в которую входят следующие данные: №, Ф. И. О. студентов, оценки за экзамены. Посчитать средний балл для каждого студента. Если сданы все экзамены и средний балл равен 5,то выплачивается 50% надбавка к минимальной стипендии, если средний балл меньше 5, но больше или равен 4, то выплачивается минимальная стипендия. Построить диаграмму, показывающую количество оценок определенного вида, полученных в данной группе.
14. Телефонная компания взимает плату за услуги телефонной связи по тарифу: 300 мин в месяц – абонентская плата 250 руб., за каждую минуту сверх нормы – 2 руб. Составить ведомость оплаты услуг телефонной связи для 10 абонентов за 1 месяц, самостоятельно указав количество потребляемого времени каждым. Найти людей с максимальной и минимальной оплатой услуг. Построить диаграмму, показывающую сравнительную характеристику сумм оплаты услуг телефонной компании каждым абонентом.
15. 10 спортсменов принимают участие в некотором соревновании. Каждый спортсмен может набрать не более 30 очков. Указать номер места, которое занял спортсмен в данном соревновании. За 1 место выплачивается премия 100000 руб., за 2 место 50000 руб. и за 3 место 30000 руб. Построить диаграмму, показывающую количество набранных очков, каждым спортсменом.
16. Составьте ведомость контроля остаточных знаний студентов по какой-либо дисциплине. Контроль остаточных знаний проходит в форме теста, по результатам которого выставляется оценка. Если студент набрал от 95 до 100 баллов, выставляется оценка «5», от 80 до 94 – «4», от 60 до 79 – «3», менее 60 – «2». Посчитайте: количество студентов, получивших оценку «5», «4», «3», «2», средний балл в группе, максимальный и минимальный баллы. С помощью диалогового окна Условное форматирование выделите все «2» красным цветом. Постройте круговую диаграмму, показывающую процентное соотношение оценок в группе.
|
|
|
Лабораторная работа № 4
Построение графиков функций
1. Запустите табличный процессор Microsoft Excel 2007.
2. На первом листе рабочей книги необходимо построить график функции y=sin(x) на отрезке [-6;6] с шагом 0,5 (рис. 32).
3. Выделите ячейки А1:F1 и объедините их, используя кнопку
 – объединить и поместить в центре на панели инструментов Выравнивание вкладки ленты Главная.
– объединить и поместить в центре на панели инструментов Выравнивание вкладки ленты Главная.
4. Введите в объединенные ячейки заголовок Построение графиков функций.
5. В ячейку А3 введите x, а в ячейку В3 – y=sin(x).
6. В ячейку А4 введите значение - 6, в А5 – значение - 5,5. Выделите эти две ячейки и наведите указатель мыши на правый нижний угол выделения – черный квадратик (маркер заполнения). После того, как указатель примет форму черного крестика, растяните область выделения до значения 6.
7. В ячейку В4 введите формулу = sin(A4) и нажмите клавишу Enter.
8. Используя маркер заполнения, скопируйте формулу в остальные ячейки.
9. Выделите значения двух столбиков и выполните команду:
вкладка ленты Вставка ► панель инструментов Диаграммы ► Точечная.
10. Приведите диаграмму к виду, представленному на рис. 32.

Рис. 32. График функции у=sin(x)
11. Переименуйте Лист1 в Графики функций.
12. Постройте на этом же листе график функции:

на отрезке [-3;3] с шагом 0,2 (рис. 33).
Для того чтобы записать функцию y воспользуемся логической функцией ЕСЛИ (Логическое выражение; значение_если истина; значение_если ложь).
Функция ЕСЛИ проверяет выполняется ли условие, и возвращает одно значение, если оно истинно и другое значение, если нет.
В нашем случае если x Î[-1;1], то y = 1–x2, в противном случае y = | x |–1.
Чтобы записать условие x Î[-1;1] воспользуемся логической функцией
И (логическое выражение1; логическое выражение2; …).
В нашем случае получим И(С3 >= – 1;С3 <= 1).
Таким образом формула для нахождения значения функции будет выглядеть следующим образом:
= ЕСЛИ (И (С3 >= – 1;С3 <= 1); 1 – С3*С3; ABS (С3) – 1).
Для вычисления модуля используется функция ABS (число).

Рис. 33. График функции
13. На втором листе рабочей книги самостоятельно постройте еще 2 графика:
y = |x2+5x-10|, [-10;5], шаг 0,5
и
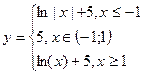 , [-3;3], шаг 0,5.
, [-3;3], шаг 0,5.
Индивидуальные задания
Постройте графики функций.
| 1. | y = x5+x2–10, [-10;10], 
|
| 2. | y = |tg(x)|×x, [-1;1], 
|
| 3. | y = cos(x+x5)–2, [-2;2], 
|
| 4. | y = |x3+x –10|, [-2;2], 
|
| 5. | y = ex-3, [-1;1], 
|
| 6. | y = ex·|x|, [-1;1], 
|
| 7. | y = cos(x3)–5, [-2;2], 
|
| 8. | y = x4-x2–х, [-5;5], 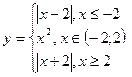
|
| 9. | y = |x|, [-10;10], 
|
| 10. | y = |x|+5, [-10;10], 
|
| 11. | y = tg(x), [-1;1], 
|
| 12. | y = x3–2x2+5, [-10;10], 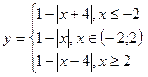
|
| 13. | y = 3cos(x)·sin(2x+3), [-10;0], 
|
| 14. | y = |x2+2x-5|, [-3;3], 
|
| 15. | y = ex2-10, [-2;2], 
|
| 16. | y = x3 – 5x–15, [-2;2], 
|
| 17. | y = |tg(x)|, [-1;1], 
|
| 18. | y = x3+5×|х|, [-5;5], 
|
| 19. | y = |3tg(x)×cos(x)|, [-1;1], 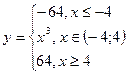
|
| 20. | y = |x2+5x-10|, [-10;5], 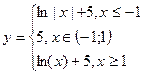
|
Лабораторная работа № 5
Решение систем линейных уравнений
I Решение систем линейных уравнений методом Крамера.
Пусть задана система линейных уравнений

Неизвестные x1, x2, …, xn вычисляются по формулам:

D – определитель матрицы А,
Di – определитель матрица, полученный из матрицы А путем замены i -го столбца вектором b.
 ,
,  ,
,  ,
,  ,
,
 .
.
Пример 1. Решить систему линейных уравнений методом Крамера.

Запишем в табличном процессоре Microsoft Office Excel 2007 матрицы, которые понадобятся нам при вычислениях (рис. 43).

Рис. 43. Исходные данные
Найдем определители D, D1, D2, и D3, используя математическую функцию МОПРЕД (рис. 44).
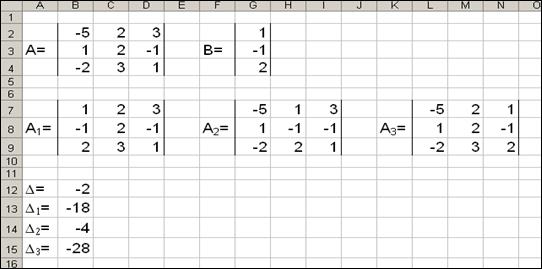
Рис. 44. Вычисление определителей
Корни уравнения найдем по формулам: 
В результате всех вычислений должны получиться следующие данные:
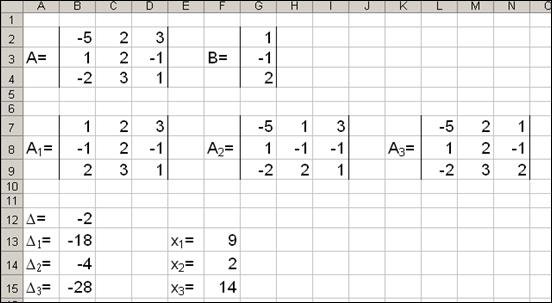
Рис. 45. Вычисление корней системы уравнений
II Решение систем линейных уравнений матричным методом
Пусть дана система линейных уравнений

Эту систему можно представить в матричном виде: А·Х=В, где
 ,
,  ,
,  .
.
Умножим систему линейных алгебраических уравнений А·Х=В слева на матрицу, обратную к А. Тогда система уравнений примет вид:
А-1·А·Х=А-1·В.
Так как А-1·А=Е (единичная матрица), то получим Е·Х=А-1·В.
Таким образом, вектор неизвестных вычисляется по формуле: Х=А-1·В.
Пример 2. Решить систему линейных уравнений матричным методом.

Запишем в табличном процессоре матрицу А и столбец свободных
членов В (рис. 46).

Рис. 46. Исходные данные
Нам необходимо найти обратную матрицу А-1, для этого:
1. выделите диапазон ячеек В8:D10;
2. вызовите функцию МОБР;
3. в появившемся диалоговом окне заполните поле ввода Матрица. Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица, то есть В2:D4, нажмите кнопку ОК;
4. В первой ячейке выделенного диапазона появиться некоторое число. Чтобы получить всю обратную матрицу, необходимо нажать клавишу F2, для перехода в режим редактирования, а затем одновременно клавиши Ctrl+Shift+Enter (рис. 47).

Рис. 47. Обратная матрица
Осталось найти вектор неизвестных по формуле Х=А-1·В, для этого:
1. выделите диапазон ячеек G8:G10;
2. вызовите функцию МУМНОЖ;
3. в поле для первой матрицы укажите диапазон В8:D10;
4. в поле для второй матрицы укажите диапазон G2:G4;
5. нажмите кнопку ОК.
В результате должны получиться следующие значения:

Рис. 48. Вычисление корней системы уравнений
Самостоятельно сделайте проверку, для этого умножьте матрицу А на Х. В результате должен получиться столбец В.
Индивидуальные задания
Решите систему линейных уравнений:
а) методом Крамера;
b) с помощью обратной матрицы.
Сделайте проверку.

| 
| ||

| 
| ||

| 
| ||
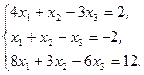
| 
| ||

| 
| ||
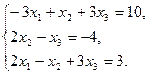
| 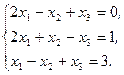
| ||

| 
| ||
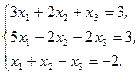
| 
| ||

| 
| ||

| 
|
|
|
|


