Теория подобия в гидромеханике

Для изучения сложных гидродинамических явлений прибегают к модельному эксперименту. Результаты таких экспериментов могут быть перенесены на натуру лишь тогда, когда явления при моделировании и в натурных условиях подобны. Различают три вида подобия: геометрическое, кинематическое и динамическое.

Для геометрического подобия требуется, чтобы отношение сходственных линейных размеров натуры L₁ и модели L₂ было равно постоянной величине

L₁/ L₂ = S₁^1/2/ S₂^1/2 = V₁^1/3/ V₂^1/3 = C_l,

где S₁, S₂ - сходственные площади натуры и модели; V₁,V₂ -сходственные объемы натуры и модели; C_l - постоянная геометрического подобия.

Кинематическое подобие возможно, если отношение промежутков времени, в течение которых сходственные точки описывают геометрически подобные отрезки траекторий, равно постоянной величине и, кроме того, выполняется геометрическое подобие натуры и

 

модели. Кинематическое подобие характеризуется двумя постоянными подобия - геометрической C_l и времени C_t = t₁/ t₂; все остальные его постоянные являются производными от указанных двух. Например, для отношения скоростей и ускорений можно записать:

υ₁/ υ ₂ = C_υ = C_l / C_t; α₁/ α ₂ = C _α = C _υ / C_t = C_l / C_t² = C_υ²/ C_l

При динамическом подобии требуется, чтобы отношение сходственных сил и натуры и модели было равно постоянной величине. Для выполнения этого условия достаточно, чтобы при наличии кинематического подобия отношение сходственных масс натуры и модели было равно постоянной величине С_m:

С_m = m₁ / m₂ = ρ₁V₁/ ρ₂V₂ = C_ρ C_l³

где ρ₁, ρ₂ - плотности сходственных объемов натуры и модели;

С_m, C_ρ, C_l - постоянные подобия.

Для отношения сходственных сил можно записать:

F₁/F₂ = m₁ α₁ / m₂ α₂ = C_ρ C_l³ C_υ ² / C_l = C_ρ C_l² C_υ ²,

Откуда следует общий закон механического подобия:

F₁/ ρ₁ υ₁² S₁ = F₂ / ρ₂ υ₂² S₂ .

Поэтому любое механическое усилие в жидкости можно представить в виде:

F = 0,5 ζ ρ υ² S,

где ζ - безразмерный коэффициент силы, который одинаков для динамически подобных явлений.

Кроме общих условий динамического подобия для сил, обусловленных вязкостью жидкости, должно соблюдаться равенство чисел Рейнольдса (подобие по Рейнольдсу)

υ₁ L₁/ ν₁ = υ₂ L₂/ ν₂ = Re

(ν₁,ν₂ - кинематические вязкости жидкостей, в которых испытываются натура и модель), а для сил обусловленных весомостью жидкости - равенством чисел Фруда (подобие по Фруду)

υ₁ / = υ₂ / = Fr.

Основы теории крыла

Гребные винты, рули, и другие судовые устройства имеют общий принцип действия, рассматриваемый в теории крыла. Для изучения работы этих устройств необходимо иметь представление о силах, действующих на крыло при движении.

Геометрические характеристики крыла определяются (рис.5.):

 

- площадью крыла F и формой проекции крыла в плане;

- длиной (размахом) крыла l - размером крыла в направлении,

перпендикулярном набегающему потоку;

- профилем крыла - сечением крыла плоскостью, перпендикулярной его размаху;

- хордой крыла b (шириной крыла) – отрезком прямой, соединяющей крайние точки профиля; при переменной по размаху крыла хорде вводится понятие средней хорды:

b_ср = F / l;

- максимальной толщиной профиля t – расстоянием между крайними точками профиля перпендикулярно хорде.

Часто пользуются безразмерными геометрическими характеристиками крыла:

- удлинением (относительным размахом) крыла λ = l /b_ср = l² /F или (для прямоугольного крыла) λ = l / b;

- относительной толщиной = 100 t / b - отношением наибольшей толщины профиля к длине хорды.

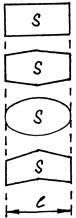
Рис.5. Геометрические характеристики крыла

 

Гидродинамические характеристики крыла (рис.6.) определяются его геометрией и углом α между хордой профиля крыла и направлением скорости движения его, называемым углом атаки. Поток, набегающий на крыло со скоростью υ под углом атаки α, на верхней поверхности крыла ускоряется, а на нижней - замедляется. Согласно уравнению Бернулли, на нижней поверхности создается повышенное давление, а на верхней - пониженное. Кроме сил давления, на движущееся в вязкой жидкости крыло действуют касательные силы трения. Силы гидродинамического давления и касательные силы трения приводятся к главному вектору гидродинамических сил Р.

 

 

 

Рис.6. Схема действия потока жидкости на крыло

 

Спроектировав главный вектор на направление движения и перпендикулярное ему направление, получим силу профильного Р_x и подъемную силу крыла Р_у:

Р_x = Р cos(Р, x); Р_у= Р cos(Р, y).

Также можно определить составляющие силы Р направленных по нормали и по касательной к крылу. Нормальная составляющая силы Р:

Р_n = Р_y cos α + Р_х sin α;

Тангенциальная составляющая силы Р:

Р_t = Р_x cos α - Р_y sin α;

Точка приложения силы Р называется центром давления. Центр давления отстоит от передней кромки крыла на расстоянии х_р. Момент относительно передней кромки крыла М = Р_n х_р.

Отношение подъемной силы крыла к его сопротивлению называется коэффициентом гидродинамического качества крыла

К = Р_y / Р_х = С _y / С_х.

Коэффициент обратного качества ε = Р_х/ Р_y.

В соответствии с общей формулой для гидродинамических сил определяется силы и моменты, действующих на крыло при движении:

Р_y = 0,5 С _y ρ υ² F; Р_x = 0,5 С _x ρ υ² F;

Р_n = 0,5 С _n ρ υ² F; Р_t = 0,5 С _t ρ υ² F;

M = 0,5 С _m ρ υ² F b,

где С_y, С_x, С_n, С_t, С_m - безразмерные коэффициенты подъемной силы, сопротивления, нормальной силы, касательной силы и момента. Отношение абсциссы центра давления крыла к длине хорды х_р / b = С _р, называется коэффициентом центра давления крыла, тогда

С _m = С _n С _р.

 

Безразмерные коэффициенты определяют гидродинамические характеристики крыла. Обычно задают независимые коэффициенты: С_y, С_x , С_m (С_р), так как остальные коэффициенты являются зависимыми.

Для данного крыла коэффициенты С_y,С_x, С_n,С_t, С_р,С_m , К(ε) зависят от угла атаки α, чисел Рейнольдса Re, Фруда Fr, а также от условий движения крыла (в безграничной жидкости, вблизи свободной поверхности жидкости, кавитации и т.п.). Они определяются теоретическим или чаще экспериментальным путем, поэтому для геометрически подобных крыльев они задаются в функции от угла атаки при установившемся обтекании потоком жидкости с некоторым числом Re. Значения гидродинамических коэффициентов крыла, в общем случае завися от числа Re, однако, при обтекании крыла без кавитации безграничным потоком несжимаемой жидкости с числом Re > (1,31,5) 10⁶ коэффициенты оказываются в автомодельной области и их можно считать независимыми от Re.

На рис.7. приведены кривые зависимости гидродинамических характеристик крыла от углов атаки. Из рисунка видно, что коэффициент подъемной силы с увеличением угла атаки вначале возрастает, а затем, достигнув максимума при так называемом критическом угле атаки α_кр, начинает резко падать. Для симметричного профиля подъемная сила становится равной нулю при нулевом угле атаки, для несимметричного -при значениях α, отличных от нуля. Угол атаки, при котором С_y обращается в нуль, называют углом нулевой подъемной силы α₀, а угол α_i = α + α₀ - гидродинамическим углом атаки. Направление потока, соответствующее углу α₀, называется направлением нулевой подъемной силы.

 

Рис.7. Кривые зависимости гидроди-намических характеристик крыла от углов атаки

 

Из рис.7. следует, что существует такое значение угла атаки, при котором коэффициент обратного качества минимальный. Этот угол называют наивыгоднейшим углом атаки α_орt.

На гидродинамические характеристики крыла сильно влияют границы потока (рис.8). Влияние твердой стенки под крылом приводит к увеличению коэффициента его подъемной силы, а по мере уменьшения погружения крыла к заметному снижению величины С _y.

 

Рис.8. Графики влияния твердой стенки и свободной поверхности жидкости на С _y прямоугольных крыльев.

 

Глава 3

Геометрия корпуса судна

 

Теоретический чертеж

 

Ввиду сложности формы обводы корпуса задаются графически в виде теоретического чертежа. На теоретическом чертеже изображены проекции на главные взаимно перпендикулярные плоскости линии пересечения теоретической поверхности корпуса с плоскостями, параллельными главным плоскостям. Под теоретической поверхностью понимают внутреннюю поверхность обшивки корпуса (без учета толщины обшивки и выступающих частей). Исключения составляют суда с деревянными и пластмассовыми корпусами, для которых на теоретическом чертеже изображают наружную поверхность корпуса.

 

В качестве главных плоскостей принимают:

- диаметральную плоскость (ДП) - вертикальную продольную плоскость, делящую корпус судна на две симметричные части - правую (правый борт) и левую (левый борт);

- плоскость мидель шпангоута (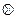) - вертикальную поперечную плоскость, проходящую по середине длины судна и делящую корпус на носовую и кормовую части;

- основную плоскость (ОП) - горизонтальную плоскость, проходящую через нижнюю точку теоретической поверхности корпуса судна в плоскости мидель-шпангоута.

Линии пересечения теоретической поверхности корпуса с плоскостями параллельным ДП называют батоксами, с плоскостями параллельными ОП - теоретическими ватерлиниями (ВЛ), с плоскостями, параллельными плоскости мидель–шпангоута - теоретическими шпангоутами.

Линии пересечения ОП с ДП и ОП с плоскостью мидель-шпангоута дают продольную и поперечную основные линии.

Пересечение ДП с корпусом образуют линию киля, форштевня, ахтерштевня и верхней палубы.

Совокупность проекций батоксов, теоретических ватерлиний и шпангоутов на ДП называется боком, на ОП - полуширотой, на плоскость мидель - шпангоута - корпусом. Эти три вида и составляют теоретический чертеж судна (рис. 9).

Рис.9. Теоретический чертеж судна

 

Каждое сечение проектируется на одну из плоскостей в своем истинном виде, а на две другие в виде прямых линий. Например, на виде «бок» в истинном виде представлены батоксы, а теоретические шпангоуты и ватерлинии в виде прямых. Из последних выделяют

 

конструктивную ватерлинию (КВЛ), по которую судно плавает с полной нагрузкой по проектную осадку. Любая другая ватерлиния, соответствующая конкретному случаю нагрузки называется действующей (расчетной) и обозначается (WL).

Число теоретических шпангоутов, как правило, принимается равными 11 или 21, которые образуют соответственно 10 или 20 теоретических шпаций.

Линии пересечения диаметральной плоскости с вертикальными поперечными плоскостями, проходящими через крайнюю носовую точку КВЛ и точку ее пересечения с осью баллера, называется соответственно носовым (НП) и кормовым (КП) перпендикулярами. При отсутствии баллера кормовой перпендикуляр получают, проводя вертикальную поперечную плоскость на расстоянии 97% длины судна по КВЛ от носового перпендикуляра.

 

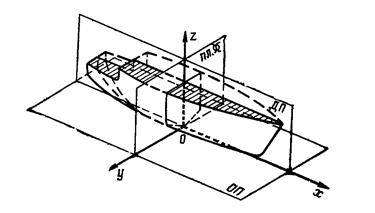
Рис.10. Главные плоскости теоретического чертежа

 

Для расчета статики судна используют прямоугольную систему координат oxyz (рис. 10). Координатные плоскости системы oxyz совпадают с диаметральной плоскостью (ДП) xoz, плоскостью мидель - шпангоута yoz и основной плоскостью xoy. Начало координат располагают в точке 0, а оси направляют соответственно в нос, на правый борт и вертикально вверх.

Теоретический чертеж предназначен для наглядного изображения обводов корпуса, расчетного определения характеристик эксплуатационных качеств судна, разработки проектных чертежей.

Расчеты мореходных качеств судна в условиях его эксплуатации проводятся по документации, в которой используются данные, полученные из теоретического чертежа. Теоретический чертеж применяется при проведении ремонтных работ по корпусу, при доковании судна.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: