 |
Процесс замедления Времени в ОТО.
|
|
|
|
К вопросу об физической сущности процесса замедления времени в специальной и общей теориях относительности.
И.В. Злобин
Член Финляндской Астрономической Ассоциации,Хельсинки, Финляндия
Введение.
А. Эйнштейну удалось в 1905 г. В работе " К электродинамики движущихся тел " [1] сформулировать основные принципы специальной теории относительности (СТО). Позднее, в 1916 г. им же, но уже в работе " Основы общей теории относительности " [ 1 ] в окончательном виде излагается общая теория относительности (ОТО), включая и гравитацию.
Решающим аргументом в пользу справедливости построенных теорий явились, предсказанные СТО и ОТО определенные следствия и эффекты. Данные астрономических наблюдений, а так же большое число физических экспериментов, подтвердивших правильность ожидаемых явлений, способствовали позитивному укреплению новых представлений в физике.
Для нас, из всего семейства физических следствий, вытекающих из СТО и ОТО, исключительный интерес имеют две стороны одного явления. Это: релятивистское замедление Времени и зависимость хода Времени от гравитационного поля.
Думается, здесь будет не лишним напомнить, как происходит процесс течения Времени в выше упомянутых теориях.
Процесс замедления Времени в СТО.
Как известно, в специальной теории относительности рассматривается выделенный класс инерциальных систем отсчета. Эти инерциальные системы отсчета формируют некоторую совокупность одинаково равномерно и прямолинейно движущихся наблюдателей, заполняющих все пространство.
Пусть, мы наблюдаем из некоторой инерциальной системы отсчета К произвольным образом движущиеся со скоростью v относительно нас часы. Будем рассматривать это движение как равномерное. Тогда, в каждый момент времени можно ввести неподвижно связанную с движущимися часами систему координат К', которая будет являться тоже инерциальной.
|
|
|
Посмотрим, каким образом связаны между собой показания часов в системах отсчета К и К'. Дифференциалы координатного t и собственного  Времени скоррелированы следующей зависимостью
Времени скоррелированы следующей зависимостью
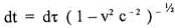 , (1)
, (1)
где с - скорость света. Из выражения (1) следует, что если 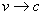 , то при фиксированном интервале
, то при фиксированном интервале 
Интегрируя формулу (1), легко найти промежуток Времени, показываемый движущимися часами, если по неподвижным часам пройдет Время 
 . (2)
. (2)
Собственное Время движущегося объекта всегда меньше, чем соотвествующий промежуток Времени в неподвижной системе. Напомним, что собственным Временем называется Время, отсчитываемое по часам движущимся вместе с данным объектом. А релятивисткий параметр  есть, так называемый,
есть, так называемый,  -фактор [2]. Он играет ключевую роль в специальной теории относительности.
-фактор [2]. Он играет ключевую роль в специальной теории относительности.
Явление, описанное нами, имеет на сегодняшний день успешное подтверждение в ряде физических экспериментов и наблюдений. Приведем одно из них, которое стало уже классическим. Время жизни  -мезона в покое составляет
-мезона в покое составляет 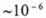 сек. Если бы, эта элементарная частица двигалась изначально со скоростью света, то расстояние, пройденное ею в верхних слоях атмосферы, не превышало бы 600 м. Однако мю-мезона, образовавшийся при столкновении космических лучей с атомами земной атмосферы на высоте нескольких километров, успевает пройти путь до поверхности Земли, где они регистрируются физическими приборами. Следовательно, с точки зрения земного наблюдателя Время
сек. Если бы, эта элементарная частица двигалась изначально со скоростью света, то расстояние, пройденное ею в верхних слоях атмосферы, не превышало бы 600 м. Однако мю-мезона, образовавшийся при столкновении космических лучей с атомами земной атмосферы на высоте нескольких километров, успевает пройти путь до поверхности Земли, где они регистрируются физическими приборами. Следовательно, с точки зрения земного наблюдателя Время  -мезона в несколько раз превышает его собственное Время.
-мезона в несколько раз превышает его собственное Время.
Процесс замедления Времени в ОТО.
Согласно существующим представлениям, в общей теории относительности выбор системы отсчета ничем не ограничен. Конгруэнция мировых линий наблюдателей представляет собой объединение кривых линий. Под конгруэнцией понимается такой класс линий, когда через каждую точку проходит одна и только одна линия. Поскольку в ОТО пространство-время искривлено, то весьма проблематично выделить в этих условиях инерциальные системы отсчета. В этом случае, направление Времени для каждого наблюдателя определяется вдоль его собственной мировой линии. Направление Времени естественно определяется касательной к мировой линии  , где
, где  - координата вдоль линии; ds - его длина [З].
- координата вдоль линии; ds - его длина [З].
|
|
|
Вследствие существования в ОТО кривизны пространства-времени будет иметь зависимость течение Времени от поля тяготения. Эта зависимость выражается в том, что Время обладает неголономностью, т.е. отсутствует единая синхронизация. Наиболее полно можно осмыслить процесс замедления Времени, если воспользоваться внешним решением Шварцшильда.
Пусть из двух наблюдателей один находится около сферы Шварцшильда  , другой - на большом расстоянии от нее
, другой - на большом расстоянии от нее  . Величину
. Величину  называют гравитационным радиусом тела, где G - гравитационная постоянная; М - масса тела; с - скорость света. Первый из наблюдателей описывает события, пользуясь метрикой Минковского в сферических координатах
называют гравитационным радиусом тела, где G - гравитационная постоянная; М - масса тела; с - скорость света. Первый из наблюдателей описывает события, пользуясь метрикой Минковского в сферических координатах
 (3)Второй - использует метрику Шварцшильда
(3)Второй - использует метрику Шварцшильда
 (4)
(4)
Обозначим через  - интервал Времени между двумя событиями, которые произошли на расстоянии r. Примем, для простоты рассуждения, что это будет промежуток Времени между двумя сигналами, которые первый наблюдатель передает второму. Последний установит, что сигналы разделены интервалом Времени dt. Здесь, Время
- интервал Времени между двумя событиями, которые произошли на расстоянии r. Примем, для простоты рассуждения, что это будет промежуток Времени между двумя сигналами, которые первый наблюдатель передает второму. Последний установит, что сигналы разделены интервалом Времени dt. Здесь, Время 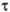 будет называться собственным Временем, а Время t - координатным. Предлположим, что геометрические координаты обоих наблюдателей остаются неизменными, т.е.
будет называться собственным Временем, а Время t - координатным. Предлположим, что геометрические координаты обоих наблюдателей остаются неизменными, т.е.  . Учитывая, что для промежутка собственного Времени интервал ds имеет вид
. Учитывая, что для промежутка собственного Времени интервал ds имеет вид  , где
, где  - временная координата,
- временная координата,  - некоторая функция от временной координаты; можно определить зависимость между дифференциалами
- некоторая функция от временной координаты; можно определить зависимость между дифференциалами 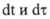 [4]
[4]
 , (5)
, (5)
 . (6)
. (6)
Интегрируя обе части равенства (6) можно найти промежутки Времени показываемые часами фиксирующими собственное и координатное Время
 . (7)
. (7)
Из выражения (5) видно, что  . Знак равенства фигурирует на бесконечности, где t совпадает с
. Знак равенства фигурирует на бесконечности, где t совпадает с 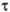 . А равенство (6) показывает, что если
. А равенство (6) показывает, что если  , то при любом конкретном интервале собственного Времени
, то при любом конкретном интервале собственного Времени  ,
,  , то собственное Время совпадает с координатным,
, то собственное Время совпадает с координатным,  .
.
|
|
|
Таким образом, на конечных расстояниях от масс происходит замедление Времени по сравнению со Временем на бесконечности.
Для проверки показаний хода часов при воздействии на них гравитационного потенциала в середине 70-х годов была проведена серия экспериментов. Можно отметить такие наиболее значительные из них - это эксперименты: Хейфеле - Китинга [5], Аллея с сотрудниками [б], а так же Вессе - Левина [7]. Результаты этих опытов подтвердили эйнштейновские предсказания.
Постановка задачи.
Сегодня, в рамках рассматриваемой проблемы, можно говорить о том, что фактически в специальной и общей теориях относительности сформулированы только причины, вследствие которых происходит интересующий нас динамический процесс. По всей видимости, скрытый внутренний механизм замедления Времени должен базироваться на физических критериях, которые тесным образом связаны с самой физической сущностью Времени.
Таким образом, суть данного исследования сводится к тому, чтобы указать на существующую возможность описать, с точки зрения геометрии, явление замедления Времени оформленное в СТО и ОТО, как процесс, который имеет одну и ту же физическую основу.
Теоретическая часть.
Прежде чем, перейти к главному, приведем общие сведения, которыми сегодня располагает физика относительно физических свойств Времени. Мы не будем останавливаться на тех физических фактах, которые как бы косвенно характеризуют различные проявления Времени. Нам прежде всего необходимо выделить такие характеристики, которые функционально связаны с самим Временем. К ним относятся: 1) Время - как форма движения материи, есть объективная реальность существующего Мира. данная нам в понимание и независящая от нашего сознания. Эта категория Природы представляет собой детерминированную систему с жесткими причинно-следственными связями. Эти связи характеризуются устойчивой консеквентной сменой таких хронологических областей, как Прошлое, Настоящее и Будущее; 2) необходимо четко понимать, что в макрофизических процесса, протекающих в окружающей нас Природе, начальные условия задаются базисом, основывающимся на необратимости Времени реального Мира [8]; 3) наблюдения показывают, что Время обладает - гомогенностью и изотропностью [9]; 4) выяснено, что в физически реалистических решениях условие каузальности и хронологическое условие эквивалентны [10]; 5) очевидно, что в ближайшей к нам области пространства-времени "стрела" Времени четко задана направлением роста энтропии квазиизолированных термодинамических систем [10].
|
|
|
После того, как мы заострили внимание на чрезвычайно важных в физическом плане понятиях, касающихся Времени, перейдем к рассмотрению основного вопроса.
Структура пространства-времени - есть, по сути дела, многообразие М, наделенное лоренцовой метрикой и определяемой ею аффиной связью [10]. По существу многообразие, в определенном смысле, может быть покрыто кусками координатных сетей. Согласно Предложению 6.4.9 [10]: условие устойчивой причинности выполняется всюду в М, если и только если существует функция f на М, grad которой всюду времениподобен. Здесь условие устойчивой причинности означает, что в каждой точке возможно немного раздвинуть световой конус, не получая при этом замкнутых временодобных кривых.
С физической точки зрения, для нас весьма ценным является появление функции f. Под функцией f прогнозируется априорный род космического Времени в том смысле, что она возрастает вдоль каждой, направленной в Будущее непространственноподобной кривой [ 10]. Представляется физически разумным предположить, что на фоне f задана непрерывным образом в каждой точке локальная термодинамическая "стрела" Времени  .
.
В обоих эйнштейновских теориях производятся операции с дифференциалами координатного Времени t и собственного Времени 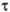 . При определенных начальных условиях этим дифференциалам при интегрировании соответствуют промежутки Времени
. При определенных начальных условиях этим дифференциалам при интегрировании соответствуют промежутки Времени 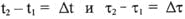 . Естественно предположить, что для разностей
. Естественно предположить, что для разностей  с достаточной степенью точности можно задать локальные "стрелы" Времени
с достаточной степенью точности можно задать локальные "стрелы" Времени  , причем
, причем  . Такая корреляция не встречает затруднений, потому что обсуждаемые параметры являются Временными характеристиками. Коль скоро,
. Такая корреляция не встречает затруднений, потому что обсуждаемые параметры являются Временными характеристиками. Коль скоро,  принадлежат космическому Времени, то и анализ будет разворачиваться в проекции на f.
принадлежат космическому Времени, то и анализ будет разворачиваться в проекции на f.
Для физического понимания основ действия механизма замедления Времени в СТО и ОТО предлагается проанализировать вариант, в котором рассматривается расположение локальных "стрел" Времени  , по отношению друг к другу, т.е. нам необходимо выяснить, как они сориентированы между собой. Ясно, что воздействие на
, по отношению друг к другу, т.е. нам необходимо выяснить, как они сориентированы между собой. Ясно, что воздействие на 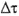 гамма-фактора (
гамма-фактора ( ) и коэффициента
) и коэффициента  генерирует эффективное изменение, что влечет за собой не равенство координатного и собственного Времени между собой.
генерирует эффективное изменение, что влечет за собой не равенство координатного и собственного Времени между собой.
|
|
|

Наиболее наглядное решение можно получить в том случае, если провести следующую процедуру. Локальные "стрелы" Времени  , ориентируются так, чтобы их начала совместились в одной точке - 0. Эта точка представляет собой полюс, такой что
, ориентируются так, чтобы их начала совместились в одной точке - 0. Эта точка представляет собой полюс, такой что  .B этом случае, разумно ожидать, что одна из локальных "стрел" Времени, например
.B этом случае, разумно ожидать, что одна из локальных "стрел" Времени, например  , будет располагаться к локальной "стреле" Времени
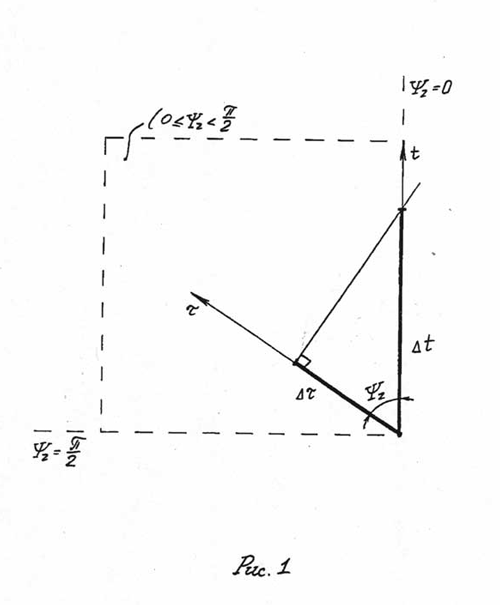
, будет располагаться к локальной "стреле" Времени  под некоторым углом (Рис. 1). В дальнейшем, для удобства рассуждения обозначим этот угол через
под некоторым углом (Рис. 1). В дальнейшем, для удобства рассуждения обозначим этот угол через 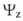 и назовем его - фазовым углом Времени, где z - это индекс, который необходим для выделения данного угла из семейства геометрических углов. Этот угол является калибровочным параметром, который позволяет установить корреляцию между исходными локальными "стрелами" Времени в том смысле, что отображение
и назовем его - фазовым углом Времени, где z - это индекс, который необходим для выделения данного угла из семейства геометрических углов. Этот угол является калибровочным параметром, который позволяет установить корреляцию между исходными локальными "стрелами" Времени в том смысле, что отображение  на
на  осуществляется посредством фазового угла Времени, т.е.
осуществляется посредством фазового угла Времени, т.е.  , где
, где 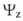 отображает
отображает 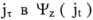 . Данный угол измеряется в двух известных системах: 1) градус, минута, секунда; 2) радиантная мера. Переходя к количественным оценкам значений промежутков Времени
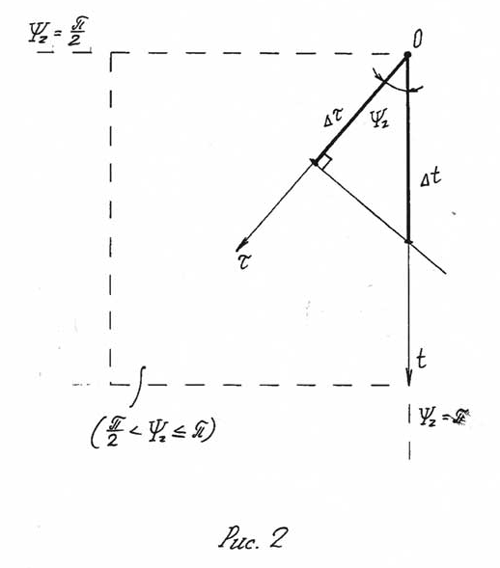
. Данный угол измеряется в двух известных системах: 1) градус, минута, секунда; 2) радиантная мера. Переходя к количественным оценкам значений промежутков Времени  необходимо схему на (Рис. 1) модернизировать соответствующим образом (Рис. 2). Проведем к концу локальной "стрелы" Времени
необходимо схему на (Рис. 1) модернизировать соответствующим образом (Рис. 2). Проведем к концу локальной "стрелы" Времени  ортогональную линию так, чтобы она одновременно пересекла конец локальной "стрелы" Времени
ортогональную линию так, чтобы она одновременно пересекла конец локальной "стрелы" Времени  . Назовем эту линию - нормалью Времени и обозначим через
. Назовем эту линию - нормалью Времени и обозначим через  . Нормаль Времени должна отвечать следующим условиям: эта линия всюду перпендикулярна собственному Времени
. Нормаль Времени должна отвечать следующим условиям: эта линия всюду перпендикулярна собственному Времени 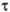 и всегда пересекает координатное Время
и всегда пересекает координатное Время  .
.

Используя известные соотношения, легко установить зависимость между локальными "стрелами" Времени
 . (8)
. (8)
Таким образом, мы установили, что локальные "стрелы" Времени связаны между собой тригонометрической функцией - секонс. Напомним два важных свойства этой функции:
1) разложение в
ряд 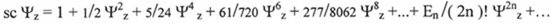 ,
,
где область сходимости  - числа Эйлера;
- числа Эйлера;
2) функция комплексного переменного
 , где период -
, где период -  ; функция на всей открытой
; функция на всей открытой
плоскости нулей не имеет.
Учитывая, что локальные "стрелы" Времени пропорциональны соответствующим им промежуткам Времени  , то аналогичная закономерность будет иметь место и для дифференциалов координатного и собственного Времени
, то аналогичная закономерность будет иметь место и для дифференциалов координатного и собственного Времени
 . (9)
. (9)
Задавая верхние и нижние пределы интегрирования можно найти интересующие нас интервалы Времени
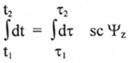 . (10)
. (10)
Из соотношения (9) вытекает, что если  ,то при заданном промежутке собственного Времени
,то при заданном промежутке собственного Времени 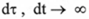 ; и если
; и если  .
.
Целью введения фазового угла Времени и функции обеспечивающей его привязку к естественным природным процессам, является предположение о том, что в общей и специальной теориях относительности явление замедления Времени имеет одну и ту же физическую основу, т.е. на прямую имеет место связь между 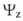 , СТО и ОТО. Эта связь выражается в том, что существует схема вида
, СТО и ОТО. Эта связь выражается в том, что существует схема вида

В первой части мы рассмотрели только теоретические аспекты проблемы. Все расчеты и практические результаты будут проведены во второй части одноименной работы.
Дополнение: напомним математические свойства, которыми обладает тригонометрическая функция - секонс 
1)  ;
;
2) функция 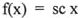 - нулей вообще не имеет, как при действительных, так и при комплексных значений аргумента [11]
- нулей вообще не имеет, как при действительных, так и при комплексных значений аргумента [11]  ;
;
3)  ;
;
4) 
5)  имеет асимптоты при
имеет асимптоты при 
1. А. Эйнштейн, Собрание научных трудов, Т. 1 / Под. ред. И. У. Тамма, Я. А.Смородинского, Б. Г. Кузнецова, - М., Наука, 1965 - 1967.
2. Дж. Нарликар, Неистовая Вселенная, М., Мир, 1985.
3. Ю. С. Владимиров, Пространство - время: явные и скрытые размерности, М., Наука, 1989.
4. Л. Д. Ландау, Е. М. Лифшиц, Теория поля. Изд. 6, М., Наука, 1973.
5. J. С. Hafele, R.E. Keating, Science, 177,166,168 (1972).
6. Ч. Аллей и др., В кн.: Альберт Эйнштейн и теория гравитации, М., Мир, 1979,с. 575.
7. R. F. С. Vessot, М. W. Levine, in: Gravitarione Sperimentale, ed. Bertotti В., Accademia Nazionali dei Lincei, Roma, 1977, p. 371.
8. С. М. Коротфув, Земля и Вселенная, 2,1989, с. 53.
9. Л. Д. Ландау, Е.М. Лифшиц, Механика, Изд. 3, М., Наука, 1973.
10. S. W. Hawking, G. F. R. Ellis, The Large Scale Structure of Space - Time, Cambridge University Press, 1973;
С. Хокинг, Дж. Эллис, Крупномасштабная структура пространства - время, М., Мир, 1977.
11. П.Ф. Фильчаков. Справочник по высшей математике, М., Наука, с. 645.
***
Сегодня, со всей ясностью становится очевидным, что открытый А.Эйнштейном процесс замедления Времени описанный в специальной и общей теориях относительности требует более глубокой проработки и осмысления. Необходимо разобраться и понять внутреннюю работу механизма замедления Времени, а не только знать причины вследствие, которых наблюдается асинхронное течение Времени в разных системах отсчета.
Теоретические вопросы этой проблемы были представлены в первой части одноименной работы.
Здесь же, будут предложены: серия расчетов и статистических оценок, которые дают нам возможность понять физический принцип действия внутреннего механизма замедления Времени.
Установим функциональную зависимость между:
1) скоростью v движущихся относительно нас часов и фазовым углом Времени  ;
;
2) координатой r (расстояние от сферы Шварцшильда) и так же фазовым углом Времени  . Используя выражения:
. Используя выражения:
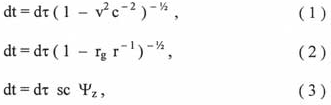
и проводя математические операции по интегрированию и составлению пропорций находим, что

1. Соотношение координатного и собственного Времени в СТО и ОТО при действии функции  , и при изменении фазового угла Времени
, и при изменении фазового угла Времени  от 0 до
от 0 до 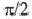 .
.
Для проведения статистического анализа необходимо задать следующие начальные условия:
1) принимаем, что с = 1 и 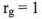 ;
;
2) выбираем, для простоты расчетов, во всех случаях (имеются в виду области, заполненные материей) собственное Время  равное, например, 10-и условным единицам. Какие именно единицы измерения (секунды, минуты, часы, дни, годы и т.д.) здесь фигурируют не столь важно, поскольку это прерогатива, например, экспериментаторов;
равное, например, 10-и условным единицам. Какие именно единицы измерения (секунды, минуты, часы, дни, годы и т.д.) здесь фигурируют не столь важно, поскольку это прерогатива, например, экспериментаторов;
3) для области изменения фазового угла Времени от 0 до 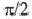 знак собственного Времени
знак собственного Времени  , естественно - положителен (+);
, естественно - положителен (+);
4) фазовый угол Времени отсчитывается в пределах  , (Рис. 1).
, (Рис. 1).
Требуется определить:
1) координатное Время в специальной теории относительности -  ;
;
2) координатное Время в общей теории относительности -  ;
;
3) координатное Время зависящее от фазового угла Времени - t, (См. Табл. 1).
Подробное обсуждение полученных данных будет сделано в разделе 3.
2. Соотношение координатного и собственного Времени в СТО и ОТО, при действии функции  , и при изменении фазового угла Времени
, и при изменении фазового угла Времени  от
от 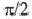 до
до  .
.
В данном разделе принимаются аналогичные начальные условия, которые указанны в разделе 1. Однако, необходимо отметить, что, здесь, фазовый угол Времени отсчитывается в границах  и собственное Время
и собственное Время  так же положительно, (Рис. 2).
так же положительно, (Рис. 2).
Как и в разделе 1 необходимо определить 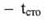 ,
, 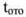 и t, (Табл. 2). Полный анализ полученных данных будет проведен в разделе 3.
и t, (Табл. 2). Полный анализ полученных данных будет проведен в разделе 3.
3. Обсуждение результатов.
В настоящее время наблюдается ярко выраженная тенденция, направленная на решение определенных физических задач с применением геометрических подходов. Эти подходы нашли широкое распространение в связи с тем, что благодаря им, можно по-новому взглянуть на ряд проблем существующих в некоторых областях физики. Не стало исключением и данное исследование, суть которого сводится к тому, чтобы используя методику естественных геометрических преобразований получить ясную картину для понимания механизма замедления Времени.
В том случае, если мы получим практически точное совпадение показаний координатного Времени  ,
, 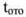 и t при фиксированной координате r, определенной скорости v и при заданном значении
и t при фиксированной координате r, определенной скорости v и при заданном значении  соответственно, то в полной мере можно говорить о том, что с физической точке зрения внутренний механизм замедления Времени имеет под собой единую основу.
соответственно, то в полной мере можно говорить о том, что с физической точке зрения внутренний механизм замедления Времени имеет под собой единую основу.
3.1. Результаты таблицы 1.
Как проводился расчет? Сначала, по формулам (4) и (5) устанавливались взаимооднозначные соответствия между текущими значениями фазового угла Времени  и конкретными величинами скорости v и координаты r. Другими словами, каждой угловой характеристике
и конкретными величинами скорости v и координаты r. Другими словами, каждой угловой характеристике  находится точное значение v и r. Зная параметры v, r и
находится точное значение v и r. Зная параметры v, r и  не трудно найти
не трудно найти  ,
, 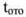 и t. Из таблиц видно, в какой степени имеет место согласование показаний Времени для трех случаев.
и t. Из таблиц видно, в какой степени имеет место согласование показаний Времени для трех случаев.
Ниже, отметим следующие интересные закономерности.
В специальной теории относительности по мере того, как скорость v устремляется к скорости света, где с = 2,997924562х1010 см/сек [2], будет наблюдаться нарастание незначительных отклонений в показаниях часов t и  , в первом знаке после запятой. Например, при v = 0,9998476 с, что составляет 99,984759% скорости света и при
, в первом знаке после запятой. Например, при v = 0,9998476 с, что составляет 99,984759% скорости света и при  = 89¦ часы соответственно будут показывать Время
= 89¦ часы соответственно будут показывать Время  = 572,78689 и t = 572,96739. Мы видим, что эти результаты одинаковые в целой части.
= 572,78689 и t = 572,96739. Мы видим, что эти результаты одинаковые в целой части.
В общей теории относительности при приближении г к  , например, г = 1,0003045
, например, г = 1,0003045  и при
и при  = 89¦ будет наблюдаться локальная несогласованность в целой части параметров Времени t и
= 89¦ будет наблюдаться локальная несогласованность в целой части параметров Времени t и 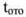 , т.е.
, т.е. 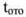 = 573,06918 и t=572,96739. Однако, используя математические правила округления десятичных дробей не трудно увидеть, что для исходного случая часы будут отсчитывать практически одинаковое Время (
= 573,06918 и t=572,96739. Однако, используя математические правила округления десятичных дробей не трудно увидеть, что для исходного случая часы будут отсчитывать практически одинаковое Время ( ). Правда, при
). Правда, при  =87¦ и
=87¦ и  = 88¦ имеем, соответсвенно,
= 88¦ имеем, соответсвенно, 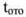 = 192,10561; t = 191,07306 и
= 192,10561; t = 191,07306 и 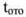 = 296,2919; t = 286,53295 фиксируется небольшой разброс в показаниях Времени в целой части t и
= 296,2919; t = 286,53295 фиксируется небольшой разброс в показаниях Времени в целой части t и 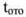 . Какое можно дать объяснение появлению подобного рода аномалий? Можно предположить, что когда значение координаты r становится сравнимым с гравитационным радиусом, то напряженность гравитационного поля возрастает на столько, что активно начинают сказываться топологические флюктуации. Время, да и пространство, в области с высокой кривизной находится в таком физическом состоянии, что становится весьма проблематично указать точные координаты. Так же, при выше указанных значениях фазового угла Времени, возможно происходят процессы, которые не известны физике, на сегодняший день.
. Какое можно дать объяснение появлению подобного рода аномалий? Можно предположить, что когда значение координаты r становится сравнимым с гравитационным радиусом, то напряженность гравитационного поля возрастает на столько, что активно начинают сказываться топологические флюктуации. Время, да и пространство, в области с высокой кривизной находится в таком физическом состоянии, что становится весьма проблематично указать точные координаты. Так же, при выше указанных значениях фазового угла Времени, возможно происходят процессы, которые не известны физике, на сегодняший день.

Необходимо сделать следующее замечание. С большой долей вероятности, можно говорить о том, что область изменения фазового угла Времени от 0 до 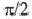 проецируется на световой конус Будущего некоторого события р (Рис.3). Схема на Рис.3 с небольшим дополнением заимствована из [1]. Выше представленная позиция справедлива, как для специальной, так и для общей теории относительности. Хотя, в ОТО имеется один нюанс, который выражается в том, что метрика g, задающая световой конус, вообще-то, меняется от точки к точке. Подобная ситуация приводит к несовпадению, в ряде случаев, пространства-времени и топологии евклидового пространства R4 [1]. В данном анализе мы рассматриваем пространство-время без замкнутых времениподобных кривых, т.е. отсутствует нарушение причинности.
проецируется на световой конус Будущего некоторого события р (Рис.3). Схема на Рис.3 с небольшим дополнением заимствована из [1]. Выше представленная позиция справедлива, как для специальной, так и для общей теории относительности. Хотя, в ОТО имеется один нюанс, который выражается в том, что метрика g, задающая световой конус, вообще-то, меняется от точки к точке. Подобная ситуация приводит к несовпадению, в ряде случаев, пространства-времени и топологии евклидового пространства R4 [1]. В данном анализе мы рассматриваем пространство-время без замкнутых времениподобных кривых, т.е. отсутствует нарушение причинности.
Приведенные табличные значения для фазового угла Времени  ;, лежащего в пределах от 0 до
;, лежащего в пределах от 0 до 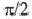 , свидетельствуют о том, что процесс замедления Времени в СТО и ОТО есть унитарное явление и внутренний механизм замедления Времени универсален для обоих эйнштейновских теорий.
, свидетельствуют о том, что процесс замедления Времени в СТО и ОТО есть унитарное явление и внутренний механизм замедления Времени универсален для обоих эйнштейновских теорий.
3.2. Результаты таблицы 2
Данные полученные в таблице 2 весьма интересны.
По аналогии с разделом 3.1, зная текущее значение  , находим v и r. Следующим шагом определяем
, находим v и r. Следующим шагом определяем  ,
, 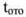 и t. В таблице наглядно демонстрируется степень реальной корреляции найденных характеристик.
и t. В таблице наглядно демонстрируется степень реальной корреляции найденных характеристик.
Из данной таблице выделим две строки, где наблюдается частичное не совпадение в целой части параметров  ,
, 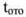 и t. Укажем их:
и t. Укажем их:
1) при  = 91¦, что соответствует скорости v = - 0,999847 с и координате г =1,0000859 rg Время измеренное на часах равно tcro = 572,78689;
= 91¦, что соответствует скорости v = - 0,999847 с и координате г =1,0000859 rg Время измеренное на часах равно tcro = 572,78689;
toTo= 1078,9581 и t =-573,00022;
2) при Tz = 93¦, скорость v = - 0,9986294 с и координате г =1,002717  Время оценивается, как
Время оценивается, как  = 191,06138;
= 191,06138; 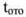 = 192,10561 и t =191,07306. В первом случае расхождения составляют между: a)
= 192,10561 и t =191,07306. В первом случае расхождения составляют между: a)  и
и  ; б)
; б)  и
и  ; в)
; в) 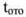 и
и 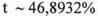 . Во втором случае имеет место незначительное расхождение, так:
. Во втором случае имеет место незначительное расхождение, так:
a)  и
и 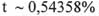 ; б)
; б)  и
и  ; в)
; в) 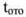 и
и 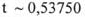 . Естественно, что для простоты рассуждений t берется по модулю. Для объяснения полученных аномалий используем гипотезу предложенную при обсуждении результатов таблицы 1.
. Естественно, что для простоты рассуждений t берется по модулю. Для объяснения полученных аномалий используем гипотезу предложенную при обсуждении результатов таблицы 1.
Переходя к главному, хочется акцентировать внимание на таких положениях.
В условиях, когда фазовый угол Времени  изменяется от 90¦ до 180¦, скорость v становится, с одной стороны, отрицательной величиной, а с другой - скорость v, взятая по модулю, не превышает по величине скорость света, | v | < с.В контексте сказанного, разумно предложить общеизвестные гипотезы, в связи с доминированием у v знака минус. Первая - координатная система К' переходит в режим равнозамедленного движения (замедление представляет собой отрицательное ускорение) относительно инерциальной системы отсчета К. Вторая - отрицательная скорость возникает в том случае, если будет превалировать движение инерциальной системы отсчета К относительно координатной системы К'. Третья - с физической точки зрения очевидно, что отрицательная скорость, как кинематический критерий, интерпретируется в областях принадлежащих Прошлому.
изменяется от 90¦ до 180¦, скорость v становится, с одной стороны, отрицательной величиной, а с другой - скорость v, взятая по модулю, не превышает по величине скорость света, | v | < с.В контексте сказанного, разумно предложить общеизвестные гипотезы, в связи с доминированием у v знака минус. Первая - координатная система К' переходит в режим равнозамедленного движения (замедление представляет собой отрицательное ускорение) относительно инерциальной системы отсчета К. Вторая - отрицательная скорость возникает в том случае, если будет превалировать движение инерциальной системы отсчета К относительно координатной системы К'. Третья - с физической точки зрения очевидно, что отрицательная скорость, как кинематический критерий, интерпретируется в областях принадлежащих Прошлому.
Хорошо видно, что координата r (расстояние от гравитационного радиуса) в полной мере зависит от  . По мере изменения фазового угла Времени от
. По мере изменения фазового угла Времени от 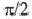 до
до  расстояние от
расстояние от  равномерно увеличивается,
равномерно увеличивается,  , переходя при
, переходя при  в бесконечность. То есть, полностью исключается ситуация, когда r может стать меньше, чем
в бесконечность. То есть, полностью исключается ситуация, когда r может стать меньше, чем  .
.
Особенно хочется выделить такой момент. Расчеты показывают, что Время t, отсчитываемое по часам связанными с действием функции секанс фазового угла Времени в границах  , образовало группу действительных отрицательных чисел. Легко заметить, что мы получили хорошо известную в физике математическую операцию - операцию обращения Времени, т.е.
, образовало группу действительных отрицательных чисел. Легко заметить, что мы получили хорошо известную в физике математическую операцию - операцию обращения Времени, т.е.  . Причем, в данном случае, инверсия Времени происходит не "искусственным" путем, а в результате строгих математических действий.
. Причем, в данном случае, инверсия Времени происходит не "искусственным" путем, а в результате строгих математических действий.
С физической точки зрения, полученная выше процедура априори адекватна тем следствиям, вытекающим из операции обращения Времени, которые известны в физике. Главное - это выполнение условия сохранения определенной симметрии, а так же ряда других условий [3].
И так главное, что хотелось бы выделить. Мы специально приводим данные для  и
и 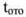 в таблице 2. Это необходимо для того, чтобы в полной мере показать ситуацию, когда числовые значения
в таблице 2. Это необходимо для того, чтобы в полной мере показать ситуацию, когда числовые значения  и
и 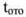 на промежутке
на промежутке  , с достаточной степенью точности, эквивалентны
, с достаточной степенью точности, эквивалентны  и
и 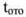 при
при  . То есть, они образовали группу действительных положительных чисел. А это значит, что выражения (1)и(2)не могут дать нам ясной физической картины. Ибо, область изменения
. То есть, они образовали группу действительных положительных чисел. А это значит, что выражения (1)и(2)не могут дать нам ясной физической картины. Ибо, область изменения  от
от 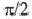 до
до  , явно проецируется на внутренность светового конуса Прошлого некоторого события р (Рис. 3). Что же касается соотношения (3), то оно без каких-либо затруднений описывает реальные физические условия в области Прошлого.
, явно проецируется на внутренность светового конуса Прошлого некоторого события р (Рис. 3). Что же касается соотношения (3), то оно без каких-либо затруднений описывает реальные физические условия в области Прошлого.
Отдельно стоит вопрос об экспликации точки  . В наших рассуждениях эта точка не входит в промежутки
. В наших рассуждениях эта точка не входит в промежутки  , т.е. она вырезана. Из расчетов видно, что
, т.е. она вырезана. Из расчетов видно, что  реально можно экстраполировать, возможно, в качестве сингулярной области.
реально можно экстраполировать, возможно, в качестве сингулярной области.
Основная динамическая сущность фазового угла Времени  , заключается в том, что он может плавно проходить все значения от
, заключается в том, что он может плавно проходить все значения от 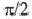 до
до  .
.
Как уже отмечалось выше, скорость света (как кинематический инвариант) связывающий пространство и Время в единое 4-мерное топологической многообразие, остается фундаментальной постоянной. Расчеты приведенные в данной работе показывают, что частиц движущихся со скоростью большей, чем скорость света (v > с) не существует. Следовательно, класс частиц относящихся к тахионам, в физически реалистических условиях, не отождествляется. Таким образом, остаются две доминирующие группы частиц - это брадионы и люксоны [4], а тахионы представляют собой брадионы и люксоны, но которые проецируются из нашего Прошлого на наше Настоящее.
Важнейший вывод вытекающий из анализа таблицы 2 это то, что при фазовом угле Времени  лежащим в промежутке
лежащим в промежутке  мы имеем Временную область - Прошлого; а значит, любое материальное тело может быть транслирование в Прошлое по отношению к Времени, например. Земли, где Время Земли выступает, как координатное Время. Но, собственное Время материального тела при этом, стабильно имеет положительное направление. И, следовательно, как хронологическое, так и причинное условия не нарушаются. Таким образом, любое материальное тело может быть перемещено в Прошлое без нарушения каузальности.
мы имеем Временную область - Прошлого; а значит, любое материальное тело может быть транслирование в Прошлое по отношению к Времени, например. Земли, где Время Земли выступает, как координатное Время. Но, собственное Время материального тела при этом, стабильно имеет положительное направление. И, следовательно, как хронологическое, так и причинное условия не нарушаются. Таким образом, любое материальное тело может быть перемещено в Прошлое без нарушения каузальности.
Подытоживая выше сказанное, хочется отметить, что для фазового угла Времени изменяющегося от 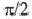 до
до  процесс замедления Времени, описанный в специальной и общей теориях отно
процесс замедления Времени, описанный в специальной и общей теориях отно
|
|
|


