 |
Изложение нового материала
|
|
|
|
Изложение нового материала по логарифмической функции необходимо проводить на двух уроках на темы: «Логарифмы и их свойства» (пункт 37 учебника), «Логарифмическая функция: свойства, график» (пункт 38 учебника). Как уже было сказано во введении к данной работе, не станем здесь переписывать материал учебников, а сосредоточимся только на собственно методических моментах [5, c. 39].
План урока изложения нового материала
· Организационный момент.
· Мотивация к изучению данной темы.
· Постановка целей, задач.
· Изложение нового материала.
· Закрепление нового материала.
· Итоги занятия, домашнее задание.
Методическая карта урока изложения нового материала
| Деятельность учителя | Деятельность учеников |
| 1. Заходит в класс и приветствует учеников. | 1. Приветствуют учителя вставанием. |
| 2. Предлагает учащимся приготовиться к уроку. а) Переходит к пункту 3. б) Дает ученикам дополнительную минуту, чтобы они приготовились к уроку. | 2. Учащиеся готовятся к уроку. а) Учащиеся готовы к уроку. б) Учащиеся не готовы к уроку. |
| 3. Проводит выявление отсутствующих. | 3. Каждый отвечает учителю, когда он называет фамилию учащегося. |
| 4. Говорит вступительные слова, тем самым мотивируя учеников к изучению данной новой темы. а) Переходит к пункту 5. б) Продолжает мотивацию, используя понятные термины, говоря об интересующих учащихся вопросах. | 4. Внимательно слушают учителя. а) Ученики готовы к восприятию нового материала. б) Ученики не готовы к восприятию нового материала. |
| 5. а) Проводит изложение нового материала. Говорит достаточно медленно и отчетливо, чтобы любой мог понять. Основные положения – диктует. б) Привлекает внимание учеников. Делает замечания отдельным ученикам. | 5. а) Записывают основные положения лекции, внимательно слушают и пытаются осознать комментарии. Записывают вопросы, чтобы задать после изложения материала. б) Ученики не слушают учителя. |
| 6. Предлагает задать вопросы, касающиеся материала, который был изложен, возможно, недостаточно ясно. а) Предлагает другим ученикам ответить на вопросы одноклассников. б) Переходит к пункту 8. | 6. а) Задают вопросы по неясным аспектам. б) Не задают вопросы учителю. |
| 7. Корректирует ответы учеников и добивается полного понимания изложенного. | 7. Внимательно слушают и записывают основные положения. |
| 8. Предлагает задать вопросы, не затронутые в изложении, но интересующие учеников, как по данной теме, так и по непосредственно связанным темам. а) Отвечает на вопросы. б) Переходит к пункту 9. | 8. Задают интересующие их вопросы. а) Задают интересующие вопросы. б) Не задают вопросы учителю. |
| 9. Проводит закрепление нового материала путем вопросов к ученикам, касающихся изложенного материала. а) Благодарит за правильные ответы и переходит к пункту 10. б) Разъясняет ученикам моменты, которые они не поняли, добивается полного понимания темы. | 9. а) Отвечают на вопросы. б) Затрудняются ответить на вопрос или отвечают неправильно. |
| 10. Разъясняет домашнее задание. Объясняет ученикам, что необходимо иметь на уроке закрепления изученного материала (конспект сегодняшнего занятия, письменные принадлежности, калькулятор). | 10. Записывают домашнее задание, требуют объяснения в случае непонимания или неясного понимания. |
| 11. Подводит итоги занятия, благодарит за внимание, прощается с учениками. | 11. Прощаются с учителем, вставая. |
|
|
|
Закрепление материала
Закрепление материала по изучению логарифмической функции соответствует теме «Решение логарифмических уравнений и неравенств» (пункт 39 учебника).
|
|
|
План урока изложения нового материала
1. Организационный момент.
2. Постановка целей, задач.
3. Повторение материала путем проверки домашнего задания.
4. Закрепление материала.
5. Оценка знаний учеников.
6. Итоги занятия, домашнее задание.
Методическая карта урока закрепления изученного материала
| Деятельность учителя | Деятельность учеников |
| 1. Заходит в класс и приветствует учеников. | 1. Приветствуют учителя вставанием. |
| 2. Предлагает учащимся приготовиться к уроку. а) Переходит к пункту 3. б) Дает ученикам дополнительную минуту, чтобы они приготовились к уроку. | 2. Учащиеся готовятся к уроку. а) Учащиеся готовы к уроку. б) Учащиеся не готовы к уроку. |
| 3. Проводит выявление отсутствующих. | 3. Каждый отвечает учителю, когда он называет фамилию учащегося. |
| 4. Говорит вступительные слова, объясняет ученикам, что будет происходить на сегодняшнем уроке. Объясняет цели, задачи урока. | 4. Внимательно слушают учителя. Осознают цели, задачи урока. |
| Проверяет домашнее задание. а) Слушает выступления учеников. б) Выясняет причины невыполнения домашнего задания, разъясняет ученикам суть домашней работы, предлагает оставить работу на следующее занятие. | 5. а) Выборочно 2 – 3 ученика отвечают домашнее задание. б) Учащиеся не выполнили домашнее задание. |
| 6. Предлагает ученикам просмотреть конспект и повторить содержание в течение 2 – 3 минут. | 6. Повторяют конспект прошлого занятия. |
| 7. Проводит оценку знаний теоретического материала в форме теста: раздает ученикам карточки с вопросами теста, разъясняет смысл задания. | 7. Отмечают в карточках правильные ответы, а, где необходимо, дополняют суждение или пишут правильный ответ. Сдают заполненные карточки теста учителю. |
| 8. Разъясняет ученикам метод решения задачи на платежную матрицу. а) Благодарит учащихся за внимание и переходит к пункту 11. б) Переходит к пункту 9. | 8. а) Осознают ход решения и записывают основные положения. б) Не понимают ход решения задачи. |
| 9. Предлагает ученикам задать вопросы по задаче, добивается полного понимания хода решения. | 9. Задают вопросы, спрашивают неясные моменты. |
| 10. Отвечает на вопросы учеников. | 10. Внимательно слушают ответы и разъяснения. |
| 11. Проводит самостоятельную работу: раздает ученикам карточки задания, чистые листы, разъясняет смысл задания. а) Благодарит учащихся за проделанную самостоятельную работу. б) Работа считается выполненной. Выясняет причины невыполнения учениками задания, предлагает одноклассникам помочь неуспевающим ребятам. в) Работа считается невыполненной. Выясняет причины невыполнения учениками задания, предлагает заняться данными вопросами дополнительно. | 11. а) Пишут ответы на вопросы. Сдают карточки с вопросами и листы с ответами учителю. б) Не более чем 20 % учеников затрудняются ответить на вопросы самостоятельной работы и отказываются сдать листы с ответами. в) Более чем 20 % учеников затрудняются ответить на вопросы самостоятельной работы и отказываются сдать листы с ответами. |
| 16. Выставляет оценки за активность на уроке. | 16. Молча слушают подведение итогов занятия. |
| 17. Объясняет ученикам, где и когда можно будет узнать результаты самостоятельной работы и теста. | 17. Запоминают или записывают. |
| 18. Подводит итоги занятия, благодарит за внимание, прощается с учениками. | 18. Прощаются с учителем, вставая. |
|
|
|
Контрольный урок
Если при описании предыдущих уроков мы не приводили теоретический материал и задачи, т.к. они содержатся в учебнике, то описание контрольного урока осуществим подробно с приведением полных текстов тестовых, теоретических и практических заданий (задач).
Цель урока: Проверить теоретические и практические знания учащихся.
На момент проведения урока – проверки знаний уровень знаний у отдельных групп учащихся различен. Но тема изучена, большинство учащихся имеют хорошие навыки решения логарифмических уравнений и неравенств.
Цели урока:
1. Обобщить и закрепить понятия логарифмической функции, свойств этой функции, свойств логарифма.
2. Проверить умения в применении этих понятий при решении уравнений, неравенств.
3. Создать деловую атмосферу, поддерживать состояние успешного продвижения в изучении темы.
|
|
|
План урока:
1. Устная работа
2. Тест
3. Проверочная работа
4. Теория зачета
5. Практика зачета
Основной метод работы на уроке: самостоятельная деятельность, диалог с учителем. После каждого проделанного задания ученик встает и кладет листок с решением в соответствующий конверт. При этом движении происходит переключение внимания с одного вида деятельности на другой и кратковременный отдых.
Раздаточный материал:
1. Карточки с тестами
2. Карточки с заданиями проверочной работы
3. Карточки зачета
4. Листы бумаги
Критерии оценки деятельности. На уроке можно получить две отметки по пятибальной системе:
Первая отметка – тест, проверочная работа
Вторая отметка – теоретическая и практическая часть зачета
При традиционной форме обучения «учитель рассказывает и решает – ученик слушает и смотрит» часть учащихся выпадет из поля зрения учителя и из процесса обучения. Предложенная технология погружает ученика в атмосферу самостоятельной работы, где роль учителя становится наводящей и консультирующей. Тем самым ученик и учитель становятся партнерами в обучении. И ответственность за процесс обучения ученик принимает на себя. Тематический план позволяет ученику распределить свои силы и время в соответствии со своими возможностями [5, c. 43]..
Ход урока:
Тестовые задания 5-7 минут.
Проверочная работа 10-15 минут.
Выполнившие все задания проверочной работы отвечают теорию по карточке зачета (номер карточки ученик наугад берет с учительского стола).
Ответившие теорию приступают к решению задач, указанных в карточках.
1. Тест
| Задание | Ответ | ||||
| Вариант 1 | Вариант 2 | ||||
| Решите уравнение: | |||||

| |||||
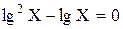
| 
| 1;100 | 1;0,1 | 1;10 | 1;0,01 |
| Решите неравенство: | |||||

| 
| 
| 
| 
| 
|
2. Проверочная работа
I
Решите уравнение: 
Решите неравенство: 
II
Решите уравнение: 
Решите неравенство: 
III
Решите уравнение: 
Решите неравенство: 
IV
Решите уравнение: 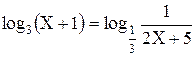
Решите неравенство: 
V
Решите уравнение: 
Решите неравенство: 
3. Работа с карточками-заданиями
Карточка 1
Сформулируйте определение логарифмической функции, определение логарифма числа. Запишите основное логарифмическое тождество.
Найдите область определения функции

Упростите выражение

Решите систему уравнений

Решите неравенство

Карточка 2
Расскажите план построения графика логарифмической функции. Приведите пример
Найдите область определения функции

Что больше:
 или
или  ?
?
Решите уравнение

Постройте график функции
|
|
|
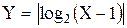
Карточка 3
Расскажите свойства логарифмической функции, иллюстрируйте на примерах
Постройте график функции 
Найдите Х, если 
Решите систему уравнений

Решите неравенство

Карточка 4
Докажите теорему о логарифме произведения
Решите неравенство

Решите уравнение

Решите систему уравнений

Решите неравенство

Карточка 5
Докажите теоремы о логарифме частного и степени
Постройте график функции

Решите уравнение

Решите систему уравнений

Вычислите  , зная, что
, зная, что 
Карточка 6
Запишите формулу перехода от одного основания логарифма к другому; разъясните ее роль в организации вычислений с помощью таблиц и калькулятора
Решите неравенство

Решите уравнение

Решите неравенство

Что больше:
 или
или  ?
?
Заключение
Подведем итоги проделанного в данной дипломной работе исследования.
Для описания места математических знаний в культуре личности подростка было введено в рассмотрение понятие субкультуры. Было сказано, что, с одной стороны, разные субкультуры для существования в ней личности подростка в разной степени требуют математической подготовки; с другой стороны, чем в большее количество субкультур может быть вплетена личность подростка, тем комфортнее подростку ощущать себя в системе общественных отношений. Следовательно, математика может занять достойное место в культуре личности подростка за счет того, что расширяют эрудицию подростка, открывая ему путь к богатству все большего набора субкультур.
Основные идеи предложенной в этой работе методики изучения логарифмической функции заключаются в следующем. Цели и задачи изучения логарифмической функции должны быть согласованы с целями преподавания математики в школе вообще.
Выделяют 3 уровня усвоения:
· репродуктивный – усвоение (умение воспроизводить, повторять пересказывать, писать) элемент базы знаний и решать типичные для изучаемого предмета задачи в типичных условиях.
· алгоритмично-действующий - умение использовать элементы базы знаний для решения типичных задач изучаемого предмета в новых условиях.
· творческий - умение использовать базу знаний для получения новых знаний и решения новых задач изучаемого предмета в новых условиях, в нетрадиционных ситуациях (нехватка времени, конфликт, кризис); на этом уровне усвоения, в основном, и применяются элементы эвристического метода обучения математике.
Вводится понятие базы знаний и описываются элементы базы знаний по теме «Логарифмическая функция».
Элементы базы знаний объединяются в 3 группы:
· понятия, термины, обозначения, символы;
· теоретические знания: законы, формулы, зависимости, причины, теории, модели;
· навыки теоретического обобщения и решения задач.
Кроме группировки по группам, элементы базы знаний распределяются по уровням усвоения – репродуктивному, алгоритмично-действующему и творческому – на основании чего прелагается модель усвоения элементов базы знаний при изучении логарифмической функции.
На основании модели усвоения элементов проводится описание уроков изложения нового материала, закрепления и контроля знания при изучении логарифмической функции в курсе алгебры 11 класса средней школы.
Библиографический список
2. Алгебра и начала анализа 10-11. Учебник для средних школ под редакцией А.Н. Колмогорова. – М.: «Просвещение», 1999.
3. Ангеловски К. Учителя и инновации. М.: «Наука»,1991.
4. Батурина Г., Кузина Т. Традиционная культура воспитания в национальной школе. Педагогика,1995,№2.
5. Борисенков В.П., Краевский В.В., Кутьев В.О., Турбовский Я.С. Философия образования. Педагогика,1995, № 4 с.3
6. Волошинов А. В. Математика и искусство. – М.: «Народное образование», 1999.
7. Газман О.С. Базовая культура и самоопределение личности. Базовая культура личности: теоретические и методологические проблемы. Сб.науч. тр. Под ред.Газманова О.С. М., Изд.АПН СССР, 1989,
8. Груденов Я.И. Совершенствование методики работы учителя математики. - М.: «Педагогика», 2003.
9. Ивлев Б.М., Саакян С.М., Шварцбург С.И. Дидактические материалы по алгебре и началам анализа для 11 класса. – М.: «Просвещение», 1999.
10. Карп А.П. Даю уроки математики. – М.: «Проспект», 1999.
11. Крылова Н.В. Ребенок в пространстве культуры. М., «Мысль», 1994.
12. Культурология. Под ред. Драча Г.В. Р.-на-Д., Изд. Феникс,1995
13. Математика. Программа для школы, работающей по базисному учебному плану. - М., 1999.
14. Математика. Программа для школ (классов) с углубленным изучением математики. — М., 1994.
15. Математика. Программы для общеобразовательных учреждений. — М.,1994.
16. Метельский Н.В. Психолого-педагогические основы дидактики математики. – М.: «Луч», 1997.
17. Методика преподавания математики в средней школе. Сборник статей. Составитель Петрова М.И. — М.: Учпедгиз, 1997.
18. На путях обновления школьного курса математики. М.: «Педагогика», 2002.
19. Новые педагогические и информационные технологии в системе образования // Под ред. Е.С. Полат. – М., ACADEMIA, 2001.
20. Савитская Т.П. Ребенок в культуре ХХ века. Знание-сила,1995,№4.
21. Селевко Г.К. Современные образовательные технологии. – М.: «Народное образование», 2002.
22. Психология. Словарь. М., 1990.
23. Учебные стандарты школ России под ред. В.С Леднева, Н.Д.Никандрова, М.Н. Лазутовой. – М., "Прометей", 1998.
24. Шарыгин И.Ф. Математика для школьников старших классов. — М.: «Просвещение», 1999.
25. Щадриков В.Д. Философия образования и образовательные политики. М., 1993.
26. Якиманская А.В. Способности к усвоению математики/ В кн. Развивающее обучение. – М.: «Просвещение», 2001.
|
|
|


