 |
Классификация бинарных отношений.
|
|
|
|
Пусть R - бинарное отношение, RÌY´X, где Y, X - таблицы (т.е. снова отношения)
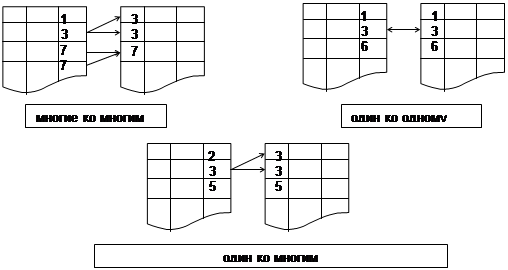
1) R - отношение "один-ко-многим", если каждому x соответствует в нем не более одного y, " xÎ X, " y,y' Î Y (R(x,y) & R(x,y') à y=y')
Пример. Отношение «человек x живет в доме y». В одном доме могут жить много людей, но каждый живет (прописан) в одном.
В этом случае таблицу Y называют материнской или родительской (parent), а таблицу X - дочерней или потомком (child ).
 |
2) R - отношение "один-ко-одному", если каждому x соответствует не более одного y, и наоборот, " xÎ X, " y,y' Î Y (R(x,y) & R(x,y') à y=y')
 Пример. Супружество, отношение «x женат на y» (европейский вариант). Каждый мужчина имеет не более одной жены и наоборот.
Пример. Супружество, отношение «x женат на y» (европейский вариант). Каждый мужчина имеет не более одной жены и наоборот.
3) Оставшиеся отношения называют отношениями "многие-ко-многим"
 |
Пример. Отношения знакомства - люди имеют много знакомых, которые, в свою очередь, тоже имеют много знакомых.
Заметим, что в последнем случае мы также имеем пример отношения - подмножества декартов квадрата, т.е. декартова произведения множества с самим собой. Такие отношения мы будем называть рефлексиями (не путать - рефлексивным отношением называют отношение, содержащее тождественное отношение).
Нетрудно заметить, что на деле эти определения соответствуют определению (графика) функции, 1-1 функции и собственного (т.е. не функционального) отношения.
Очень полезный, но реже употребляемый на практике, в силу вычислительной сложности, количественный подход к классификации отношений предусматривает оценку чисел N,M - "N записей одной таблицы может находиться в данном отношении с не более, чем M записями другой таблицы". Пропорцию N:M называют кардинальностью отношения.
|
|
|
В силу упомянутой выше большей простоты восприятия понятия функции, отношения "один-ко-многим" наиболее популярны в СУБД. Отношения "многие-ко-многим" трудны для восприятия и обработки - как правило, их стараются разложить, представить в виде соединения нескольких отношений "один-ко-многим". Отношения "один-к-одному" также достаточно редки - взаимно-однозначное соответствие "сущностей" обычно воспринимается нами как одна "сущность". Наличие связи "один-к-одному" означает (как правило), что удобнее иметь дело не с двумя, а с одним отношением (их композицией по этому соответствию).
Не случайно, в классической теоретико-множественной математики, как мы знаем, взаимно-однозначное соответствие составляет основу всякого отождествления. Заметим правда, что в приведенных выше определениях не требовалась всюду определенность (тотальность) определяемых функций. Так, весьма популярное в математике отношение "быть подмножеством" - пример отношения "один-ко-одному". В СУБД такая связь чаще применяется в случаях, когда лишь небольшое число записей одной таблице имеет соответствие в другой (т.е. является аналогом отношения “быть подмножеством”).
Реляционные БД.
Итак, изначально, база данных - модель некоторой реальности (предметной области), отражающую информацию о ней в виде совокупности связанных отношениями таблиц и ориентированная на запросы пользователей о содержащейся в ней информации - как явно, так и неявно, логически.
Еще раз отметим, что это классическое определение БД определяет структуру данных, но не преобразований, цель ее использования, но не средства ее достижения. Позже нам придется вернуться к определению БД, существенно пополнившимся в ходе практики использования СУБД. “Данные – это (не только) значения”. Как мы увидим, осознание этого фундаментального факта привело к существенному сближению и взаимообогащению понятий база (модель) данных и типа данных - как логических понятий, хотя существенная прагматическая разница между обработкой файлов и данных оперативной памяти продолжает существовать. На удивление, кажется, что описываемая ниже первоначальная эволюция СУБД от структур данных с фиксированным и неявно заданным множеством преобразований (алгоритмов доступа) к “свободным структурам данных” свидетельствует об обратном. На деле, мы увидим, что схожий процесс происходил в эволюции понятия типа данных в первоначальной интерпретации процедурном программировании к понятию класса в объектном программировании.
|
|
|
Таблицы БД естественно реализуются последовательными файлами записей.
Ощутимая разница между теоретическим определением таблицы как отношения (множества) и ее фактической реализацией как последовательности (перечислением множества) нередко вносит неопределенность в семантику операций над таблицами.
Как реализовать отношения? Кажется совершенно естественным реализовать выделенные отношения программно, снабдив БД механизмом навигации, т.е. внутренними алгоритмами прохода по связям - например, от родителя к потомкам. Именно такой навигационный подход реализовывался в ранних иерархических и сетевых БД.
В названиях отражается применяемая в таких БД структура отношений в виде дерева (каждый потомок может иметь только одного родителя) и произвольного отношения (сети) - как правило, без связей "многие-ко-многим", но с возможностью каждому потомку иметь несколько родителей (множественное наследование).
Преимуществом навигационного подхода является высокая скорость доступа при выполнении запросов, недостатком - достаточно узкий круг разрешенных запросов; принято говорить, что навигационные БД не поддерживают незапланированные запросы.
Очевидно, что кроме явно выделенных, БД всегда содержит информацию о множестве иных, вторичных и неявных, но часто очень естественных с точки зрения пользовательских запросов отношений - таковы, например отношения-рефлексии "быть однофамильцем" или "быть старше (младше, ровесником)", никак не связанные с основным отношением "живет в доме", но логически выводимые из полной структуры БД.
|
|
|
Сегодня интерес к иерархическим БД вновь возрождается в виде т.н. объектно-ориентированных БД; возникающие вновь при этом проблемы с множественным наследованием мы обсудим позже в нашем курсе по ООП. Иерархические классификации – естественный упрощающий сложные реалии жизни аппарат нашего мышления. Проблема лишь в том, что реальность богаче любой фиксированной классификации. “Родитель”, в одной классификации – скажем, бюрократической иерархии, может оказаться “ребенком” в другой – например, иерархии геналогической.
Подлинной революцией в развитии БД стали т.н. реляционные БД, в которых отношения не реализуются программно, но представляются в структуре БД с помощью специальных ключевых выражений.
Теоретический базис таких БД составила упомянутая выше реляционная алгебра Кодда.
Для полного понимания механизма ключей нам понадобится несколько определений.
Основным и, по существу, единственным структурным типом реляционных БД являются таблицы. Поля таблиц могут содержать лишь значения базовых, или скалярных типов, а также общее для всех таких типов специальное неопределенное значение NULL. В отличие от привычного описания сложных типов в процедурных языках, определение таблицы не рекурсивно и не итеративно, содержа лишь «один уровень»– таблицы не могут содержать в качестве полей другие таблицы.
А это значит, что нам придется отказаться от обычного при использовании структур оперативной памяти употребления неявного отношения включения при описании объектов, как в следующем примере
 |
Единственный способ описания нетривиальных, сложно структурированных объектов и их взаимосвязей используется - явное задание отношений.
Идея реализации отношений между таблицами в реляционных БД исключительно проста и изящна - заменить рассмотрение отношений между сложными объектами (таблицами) простыми отношениями между простыми значениями базовых типов. А что может быть проще отношения равенства?
|
|
|
Рассмотрим работу механизма ключей в случае задания отношения "один-ко-многим". Пусть PrKey(r) - некоторое выражение над полями таблицы Parent. Можно считать, что PrKey различает две записи r1,r2ÎParent, если PrKey(r1)¹PrKey(r2). PrKey называется первичным ключом (primary key) таблицы, если оно позволяет идентифицировать каждую запись таблицы, отличить ее других:
" r1,r2 Î Parent (r1=r2 Û PrKey(r1)=PrKey(r2))[1]
В самом простом – и потому часто встречающемся на практике - случае ключом таблицы служит значение одного из ее полей, называемого в этом случае ключевым; в противном случае ключ называется составным.
Согласно определению таблицы как отношения (т.е. множества), все поля записи должны образовывать ее первичный ключ - проще говоря, таблица не может содержать двух записей с полностью совпадающими значениями всех полей.
Здесь мы не уточняем определений зависящих от конкретной реляционной СУБД скалярных типов, операций над ними, равно как и точное понятие выражения. Так, в языках семейства xBase выражение-ключ – скалярного типа, а в рассматриваемом далее языке SQL таковым может быть произвольный список имен столбцов. В дальнейшем мы придерживаемся последнего, стандартного в теории БД определения.
Так, в предыдущем примере номер паспорта (но, в силу существования однофамильцев - не фамилия!) – первичный ключ таблицы ЛЮДИ, а первые три поля таблицы ДОМА (адрес дома) образуют составной первичный ключ этой таблицы.
Далее, пусть FKey(r) - выражение над полями другой таблицы Child. Запись r1, r1ÎChild ссылается (references) на запись r2, r2ÎParent, если FKey(r1)=Parent(r2). FKey называется внешним ключом (foreign key) таблицы Child, если каждая запись в Child имеет соответствие в Parent в следующем смысле:
" r1Î Child (FKey(r1) ¹NULL à $r2ÎParent (FKey(r1)=PrKey(r2))
Очевидно, отношение "один-ко-многим" R между таблицами Parent, Child можно определить заданием соответствующих ключевых выражений FKey, PrKey таких, что
" r1 Î Parent " r2 Î Child (<r1,r2> Î R Û FKey(r1)=PrKey(r2))
Аналогично, отношения "один-к-одному" могут быть заданы равенством первичных ключей, а отношения "многие-ко-многим" - равенством внешних ключей.
Как выбирать ключевые выражения? Как мы видели, во многих случаях такой ключ естественно возникает из логики задачи (номер паспорт, табельный номер и пр. - ничто иное, как уникальные идентификаторы, т.е. первичные ключи). Самый простой (а потому и самый популярный) способ "на все случаи жизни" - кодировка; можно добавить в каждую из связываемых таблиц искусственное (т.е. не связанное с логикой задачи) ключевое поле (числовой или иной код) - конечно же, следя за тем, чтобы их значения были равны для связываемых отношением записей.
|
|
|
Так, скажем, можно добавить в таблицу ДОМА поле Код, а в таблицу ЛЮДИ - ссылочное поле Дом, проставляя для каждого человека в описывающего его запись значение кода дома, в котором он живет.
 |
Наиболее тривиальный способ - добавить все поля (образующий по определению первичный ключ) родительской таблицы в таблицы дочерней явно отпадает по меньшей мере по соображениям компактности хранения (о недопустимости дублирования информации - см. далее; исключение – связь 1-1, каждый человек живет в своем доме). Так, для того, чтобы отразить в нашей модели отношения вида “(Этот) человек живет в (этом) доме”, мы должны будем внести значение первичного ключа таблицы ДОМА (адрес дома) в соответствующие поля таблицы ЛЮДИ.
 |
Пример использования кодировки для реализации отношений.
|
|
|


