 |
Выполним задания 5, 6 и 7 для построенной линейной модели множественной регрессии.
|
|
|
|
Задание 5. Расчет коэффициентов эластичности. Вычислим средние коэффициенты эластичности:


Коэффициент эластичности при факторе X3 показывает, что при изменении смертности на 1% от среднего уровня прирост населения изменится в обратную сторону на 1,03% от своего среднего уровня при фиксированном среднем числе детей в семье.
Коэффициент элестичности при факторе X5 показывает, что при изменении среднего числа детей в семье на 1% от среднего уровня прирост населения изменится в ту же сторону на 1,44% от своего среднего уровня при фиксированном уровне смертности.
Сравнивая эти коэффициенты между собой, можно сделать вывод, что среднее число детей в семье более сильно влияет на прирост населения, чем уровень смертности.
Задание 6. Проверка предпосылок использования метода наименьших квадратов:
Для исследования свойств остатков в диалоговом окне Результаты множественной регрессии →вкладка Остатки/Предсказанные/Наблюдаемые значения → кнопка Анализ остатков
а. Случайность остатков;
Для проверки случайности остатков обычно используются специальные тесты (например, тест серий). Мы убедимся в случайности остатков, построив диаграмму рассеяния, и подтвердив отсутствие тенденции.
Для построения диаграммы в диалоговом окне Анализ остатков выбираем→ вкладку Диаграммы рассеяния и кнопку Предсказанные и остатки

В результате получим диаграмму, анализ которой показывает, что зависимость е=е(y(x)) не содержит тенденции и точки располагаются вблизи оси абсцисс. Следовательно, предпосылка о случайности остатков выполняется
б. Постоянство дисперсии остатков (гомоскедастичность) (тест Гольфельда-Квандта);
|
|
|

В окне Анализ остатков → перейдем на вкладку Дополнительно → выберем кнопку Остатки и предсказанные. В результате появится таблица, два столбца из которой – Предск. значение и Остатки скопируем в буфер обмена (рис. 18)
Перейдем в таблицу с исходными данными. Добавим новые переменные. Для этого выполним команду Переменные → Добавить. В появившемся диалоговом окне укажем, что надо добавить 12 переменных после переменной Y

Рис. 18.
Далее необходимо вставить из буфера данные и переименовать переменные (например, Yt – для рассчитанных по модели значений Y, и E – для остатков). Для переименования достаточно дважды щелкнуть на имени переменной и в открывшемся окне прописать имя переменной.
Для проведения теста Гольфельда-Квандта разобъем все данные на 3 части, исключив средние 18 наблюдений. В первой группе будет 17 наблюдений с номерами с 1 по 17, во второй группе также 17 наблюдений с номерами с 36 по 52.
Рассмотрим отдельно каждый из оставшихся в модели факторов.
Упорядочить объем нашей совокупности по фактору X3 (Сортировка по
возрастанию): щелкнуть на имени переменной и выбрать кнопку сортировки 
Выйти из окна Анализ остатков – кнопка Отмена
Выйти из окна Определение модели – кнопка Отмена
В стартовом окне Множественная регрессия нажать кнопку Переменные
Выбрать в качестве факторов оставшиеся при проведении пошаговой регрессии переменные (у нас X3 и X5)
В стартовом окне Множественная регрессия нажать кнопку Select cases Y (выбор наблюдений) (рис. 19)

Рис. 19.
В появившемся окне Условия выбора наблюдений Анализа выставить необходимые флажки и включить опции, указать номера наблюдений с 1 по 17 (рис. 20). ОК

Рис. 20
В стартовом окне Множественная регрессия нажать кнопку ОК
В окне Определение модели нажать кнопку ОК
|
|
|
В окне Результаты множественной регрессии перейти на вкладку Дополнительно и нажать кнопку Дисперсионный анализ
В результате получим таблицу Дисперсионного анализа

Для прведения теста Гольфельда-Квандта нам нужна Остаточная сумма квадратов. В этой таблице она находится в строке Остатки столбца Сумма квадратов:
SS1=1,45247.
Вернемся в стартовое окно Множественная регрессия. С помощью кнопки Select cases Y
Выберем теперь наблюдения с номерами с 36 по 52. Даллее – как и для группы наблюдений с минимальными значениями X3.

Сумма квадратов остатков для выбранных наблюдений:
SS2=1,90467
Вычислим F-статистику теста Гольфельда-Квындта: 
Найдем критическое значение статистики:
Fкр=F(0,95; n1-p-1; n2-p-1)=F(0,95; 17-2-1; 17-2-1)=F(0,95;14;14)= 2,484
Так как Fв<Fкр, то гипотеза о гомоскедастичности остатков (независимость остатков от величины фактора X3) принимается.
Проведем такую же проверку по фактору X5
В результате получим:
УСЛОВИЯ ВЫБОРА НАБЛЮДЕНИЙ:
Включить наблюдение с номером: 1:17

УСЛОВИЯ ВЫБОРА НАБЛЮДЕНИЙ:
Включить наблюдение с номером: 36:52

Вычислим F-статистику теста Гольфельда-Квандта: 
Так как Fв>Fкр, то гипотеза о гомоскедастичности остатков (независимость остатков от величины фактора X5) отклоняется.
Не выполняется одна из предпосылок МНК. Необходима коррекция модели – применение обобщенного метода наименьших квадратов (ОМНК). Для этого необходимо знать аналитический вид зависимости дисперсии остатков от переменной X5.
Воспользуемся тестом Глейзера. Причем, поиск зависимости |e| от переменной X5 не дал положительных орезультатов. Поэтому было решено использовать тест Уайта. В результате было получено уравнение регрессии |e| на факторы X3 и X5.
Нахождение коэффициентов модели осуществлялось в модуле Нелинейное оценивание (хотя модель получилась линейной)

|e|= 0,4066-0,0412*X3 + 0,07237*X5; R2= 0,249.
Предсказанные значения остатков (см. таблицу ниже) необходимо скопировать в таблицу с исходными данными.

Теоретически рассчитанные остатки (только-что вставленные) назовем S. Используя их, вычислим «веса» для всех переменных модели. Для этого введем переменную P:
Pi=1/Si
Введем новые переменные PY=Y*P; PX3=X3*P; PX5=X5*P
|
|
|
Будем строить «взвешенное» уравнение регрессии:
 (*)
(*)
без свободного члена – он заменяется весовым коэффициентом Pi=1/Si.


Так как все члены уравнения (*) делятся для каждого наблюдения на одно и то же число, то уравнение можно записать в виде:
Y= 0,808-0,1451*X3+0,6194*X5. (**)
При сравнении модели из п.3 с данной, видим, что коэффициент детерминации у последней модели выше, дисперсии коэффициентов регрессии – ниже.

Предсказанные значения скопируем в исходную таблицу – назовем YY.
Для сравнения исходной модели, полученной МНК, и последней модели (ОМНК) вычислим среднюю относительную ошибку аппроксимации MAPE:

Для этого введем в исходную таблицу дополнительные столбцы:
Yтеор=YY/P – исключение «веса» из теоретически рассчитанной переменной PY
E1=y-Yтеор – ошибка последней модели
MAPE1=Abs(E1)/Yтеор - по последней (ОМНК) модели;
МAPE=Abs(E)/Yt – по модели, построенной в Задании 3.
После вычислений выделить последние два столбца (только числа), нажать ПРАВОЙ кнопкой мыши, в выпадающем меню выбрать
Блоковые статистики→по столбцам→Среднее
В результате под столбцам буду вычислены средние относительные ошибки, которые надо умножить на 100%.
Для МНК- модели MAPE= 34,56%
Для ОМНК-модели MAPE=27,01%
Скорректированная модель (**) по всем параметрам лучше, чем полученная в п.3.
в. Отсутствие автокорреляции
Отсутствие автокорреляции остатков подтверждается статистикой Дарбина-Уотсона.
Окно Результаты множественной регрессии → вкладка Остатки/Предсказанные/Наблюдаемые значения → кнопка Анализ остатков.
В окне Анализ остатков → вкладка Дополнительно → кнопка Статистика Дарбина-Уотсона

По таблицам находим значения верхней и нижней границ статистики DW
При n=52 и p=2 (два фактора в уравнении) dU=1,59 и dL=1,5. Так как DW=1,711> dU, то автокорреляция остатков отсутствует.
г. Нормальный закон распределения остатков;
Построить гистограмму остатков и подтвердить нормальность их распределения можно:
|
|
|
1) окно Анализ остатков → вкладка Остатки → кнопка Гистограмма остатков

2) использовать Графики → Гистограмма

Критические значение критерия Колмогорова-Смирнова при α=0.05 и числе наблюдений n=52 составляет Dкр = 0.188. Так как вычисленное значение статистики D=0,1366<Dкр, то гипотеза о нормальном распределении остатков принимается.
3) использовать вероятностный график остатков: окно Анализ остатков → вкладка Вероятностные графики → кнопка Нормальный
Это график остатков, построенный на специальной «вероятностной бумаге», сетка которой масштабирована так, что нормальные данные на этой сетке ложатся на прямую. На рисунке эта прямая изображена сплошной линией, а остатки – в виде точек. По рисунку видно, что точки расположены очень близко к прямой. Это еще раз подтверждает нормальность распределения остатков в последней (ОМНК) модели.

Задание 4. Построение нелинейной формы с полным набором факторов и оценку качества построенной модели
(форма модели выбирается по правилу:
0 - полулогарифмическая модель;
1 - гиперболическая модель;
2 - мультипликативная модель;
3 - экспоненциальная модель,
где 0, 1, 2, 3 - остаток от деления номера варианта на 4);
При анализе зависимости результативного признака Yот всех факторов (Задание 1, рис.13) выдвинуто предположение о линейной зависимости от факторов X1, X3, X4 и логарифмической зависимости (или параболической) от факторов X2 и X5.
То есть предполагаемая форма нелинейной зависимости:

Это смешанная (не полулогарифмическая и не мультипликативная) модель.
Ее мы построим позже.
По заданию выберем наиболее сложную для анализа - мультипликативную модель:

Преобразуем ее к линейному виду (прологарифмируем):

Введя обозначения  , получим уравнение линейной регрессии:
, получим уравнение линейной регрессии:

Для расчета параметров этого уравнения введем в основную таблицу новые переменные – логарифмы исходных данных. Для этого, во-первых, добавим в таблице переменные. Для этого выполним команду Переменные→Добавить. В появившемся окне укажем, что добавляется 10 переменных после переменной MAPE (рис. 21) → ОК

Рис. 21.
Выполним команду Переменные → Все спецификации. В появившемся окне введем имена переменных и формулы их вычисления (рис. 22)

Рис. 22
В результате в исходной таблице появятся данные для построения нелинейной модели рис. 23 (фрагмент таблицы)

Рис. 23.
Обратите внимание, что в таблице появились пропущенные значения. Это связано с тем значение переменной Y для Гонконга - отрицательное число, логарифм которого вычислен быть не может. При выполнении регрессионного анализа такие данные будут пропускаться.
|
|
|
Выполним команду Анализ→Множественная регрессия. В появившемся окне нажать кнопку Переменные. В окне «Списки зависимых и независимых переменных» слева указать зависимую переменную W, а справа – все остальные факторные переменные LX1, LX2, LX3, LX4, LX5. → ОК
Для анализа построенной модели выведем результаты – кнопка Итоговая таблица регрессии.
В результате Statistica выдает две таблицы: Итоговые статистики и Итоги регрессии


В целом уравнение регрессии значимо, коэффициент детерминации достаточно высокий, но в уравнении присутствуют незначимое параметры – коэффициенты при переменных LX1 и LX5. Нажмет кнопку Отмена. В результате попадем в стартовое окно регрессии, где необходимо выставить флажок у опции Пошаговая или гребневая регрессия (см. Задание 3, рис. 15)
Запустим процедуру пошаговой регрессии с исключением (см. Задание 3, рис. 16).
В окне Результаты множественной регрессии → выберем вкладку Дополнительно нажмем кнопки → Итоговая таблица регрессии, Дисперсионный анализ.
В результате получим несколько таблиц



Обратите внимание, что число наблюдений, по которым строилось уравнение регрессии, уменьшилось на единицу. Соответственно, и число степеней свободы, используемые для расчета критических значений tкр и Fкр, изменится.
Уравнение регрессии, полученное при пошаговой процедуре исключения, выглядит следующим образом:

Потенцируя это уравнение, получим:
(**)  , где
, где 
Замечание: Характеристики R2=0,849, Fв=135,38, Стандартная ошибка оценки Se =0,39769 относятся к регрессионной модели для объясняемой переменной W=ln y.
Нам же необходимо определить эти характеристики для переменной Y (Рис.25).
Способ 1. Используя эту формулу (**), рассчитаем теоретические значения переменной Y по нелинейной модели. Для этого в основной таблице введем новую переменную YY и определим для ее вычисления вышеприведенную формулу

Рис. 24.
Пересчитать значения исходной переменной Y можно и по-другому.
Способ 2.
На вкладке Остатки/Предсказанные/Наблюдаемые значения → кнопка Анализ остатков
В окне Анализ остатков → перейдем на вкладку Дополнительно → выберем кнопку Остатки и предсказанные. В результате появится таблица, столбец из которой – Предск. значение скопируем в буфер обмена и вставим в основную таблицу- столбец LY _ t.___
Вычислим теоретические значения переменной Y по нелинейной модели: Введем новую переменную – Y _ t (Рис.25).

Если сравнить рассчитанные двумя способами предсказанные по модели значения Y, то видим, что они различны. Это связано с ошибкой округления коэффициентов (в формуле, которую мы вводили вручную для пересчета). Способ 2 более предпочтителен, т.к. в нем нет округлений для коэффициентов. Дальнейшие расчеты будем проводить, используя данные столбца Y_t.
Теперь мы можем рассчитать основные характеристики уравнения регрессии. Для этого необходимо вычислить Е -остатки модели, сумму квадратов остатков E2, индекс детерминации квази- R2, а также относительную ошибку аппроксимации MAPE.
Введем для этого дополнительные столбцы в основную таблицу
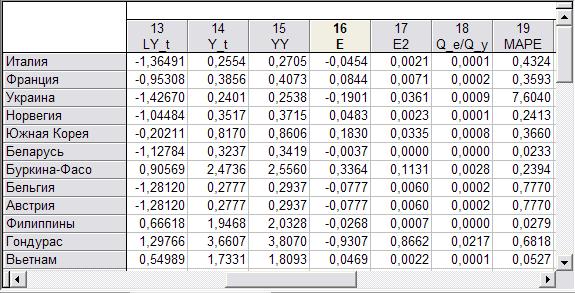
Рис.25
В столбце E вычислим ошибку модели. Для этого введем формулу E=Y-Y_t
В столбце E2 вычислим квадрат ошибки: E2=E^2. (понадобится для вычисления средней абсолютной ошибки аппроксамации - MSE, и индекса детерминации η2
В столбце Q_e/Q_y введем формулу =E2/(1,092*52).
Пояснение:

D(y)= 1,092; n =52 (по такому количеству данных вычислялась дисперсия переменной y)
В столбце MAPE введем формулу =ABS(E/Y)/51*100.
По последним трем столбцам вычислим суммы. Для этого надо выделить последние три столбца (только числа), нажать ПРАВОЙ кнопкой мыши, в выпадающем меню выбрать
Блоковые статистики→по столбцам→Сумма
В результате получим величины, необходимые для расчета характеристик качества построенной модели (рис.26).
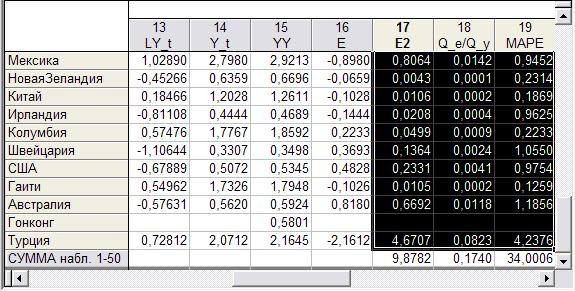
Рис. 26.
Сумму, вычисленную по столбцу E2, используем для вычисления стандартной ошибки модели:

Сумму, вычисленную по столбцу Q_e/Q_y, используем для вычисления индекса детерминации

Сумма, вычисленную по столбцу MAPE, дает среднюю относительную ошибку аппроксимации в процентах:
МAPE =34%
Дальше не сделано!!!! Расчеты аналогичные линейной модели
Задание 8. Сравните построенные модели. Выберите лучшую. Выбор обоснуйте.
(cм. Сравнение моделей в парной регрессии)
Задание 9. Выполните расчет прогнозного значения результата, предполагая, что прогнозные значения факторов составят 104,2% от их среднего уровня.
|
|
|


