Бессилие от знания или может ли история помочь физикам?

Научно - значит, опровергаемо.

Математика - наука точная и неопровержимая.

История развития физики насыщена острыми ситуациями, в процессе разрешения которых сталкиваются человеческие судьбы, и при этом проявляются величие духа одних, и очень, порой, несимпатичные свойства других ученых. С течением времени личные трагедии и заблуждения забываются, и множество отдельных, местных революций воспринимаются потомками как плавное, эволюционное, поступательное движение процесса познания. В современных учебниках излагается уже логичная и благообразная, но не история, а всего лишь информация о результатах этой эволюции.

Мне представляется, что такое сглаживание и выхолащивание истории развития науки отнюдь не способствует привлечению в научную деятельность молодежи. В самом деле, если науку действительно делали лишь непогрешимые титаны и рыцари без страха и упрека, то нужно иметь изрядное мужество, чтобы сделать попытку приобщиться к этой когорте. А вместе с тем, знание ошибок и заблуждений наших предшественников зачастую может оказаться полезным не только при обучении, но и оказать неоценимую услугу при разрешении весьма острых и вполне современных ситуаций.

Так, например, как следует из энциклопедии, "Своими экспериментами Герц подтвердил великую догадку Максвелла о распространении электромагнитной энергии в вакууме..." Что можно извлечь для себя из этой фразы? Преклонение перед гениями может вызвать в лучшем случае зависть. Пусть и белую. А ведь на самом деле все было отнюдь не так.

Не было у Герца намерения подтвердить догадку Максвелла. Но мало того, не было и у Максвелла никакой догадки по этому поводу.

Уравнения Максвелла оказались намного мудрее своего создателя. Получив чисто математически, из соображений симметрии уравнений, необходимость существования тока, протекающего в диэлектрике, Максвелл и сам этому удивился, и снабдил соответствующий этому току член уравнения индексом как бы в порядке своего извинения. Дескать, я и сам понимаю, что ток через диэлектрик течь не может, и, скорее всего, это какая-то математическая абстракция.

Были попытки и при жизни Максвелла со стороны его поклонников (весьма немногочисленных, кстати) представить этот момент как теоретическое предвидение. И надо сказать, что сам автор охлаждал пыл своих почитателей напоминанием того, что в теорию математика превращается только тогда, когда описывает экспериментально наблюдаемый факт. В данном же случае построение пока что является не теоретическим, а сугубо гипотетическим.

Вот это высший класс методологической грамотности!

А что же Герц?

Дело в том, что немецкий физик Генрих Герц был глубоко убежден, что сколько-нибудь серьезное научное открытие может быть сделано только немцами. И если с открытиями англичанина Фарадея он еще как-то мог смириться, потому что Фарадей, как известно, был слабым математиком, и все его работы были чисто экспериментальными (а следовательно, как бы второсортными), то уж шотландец Максвелл вызывал у него резкое и нескрываемое раздражение. Делом своей жизни Герц считал экспериментальное доказательство заблуждения Максвелла, и современники не раз отмечали весьма некорректные его высказывания в адрес уже покойного ученого.

К чести Герца, следует сказать, что, получив вместо опровержения экспериментальное подтверждение теории Максвелла (ибо с этого момента построение Максвелла уже являлось теорией), Герц публично принес свои извинения. Но главное во всей этой истории то, что оба ее участника одинаково относились к математике, настаивая на том, что в физике лишь та математика важна и незаменима, которая описывает реально существующие процессы. То есть когда оба высказывания, вынесенные в качестве эпиграфов, сосуществуют диалектически.

Ведь что греха таить, эта точка зрения присуща далеко не всем ученым. Сплошь и рядом, чуть приоденут мысль в математические одежды, и уже теорией называют. А то, что экспериментатор - ученый второго сорта, это мнение и сегодня в науке очень популярно.

Несмотря на то, что всем нам неоднократно приходилось слышать утверждение о том, что и эксперимент без математического осознания - тоже не наука, позволю себе с этим не согласиться. Наука, по определению Менделеева, это поиск истины. Сама же истина - уже не наука, а скорее, памятник ей.

Физика, по определению, есть не что иное, как совокупность эффектов и явлений. Уровень понимания различных эффектов очень неодинаков. И чем меньше эффект осознан, тем больший научный процесс он представляет. Абсолютно, досконально понятых и осознанных эффектов нет и быть не может в силу бесконечности познания. Вот поэтому-то у меня вызвало некоторую настороженность известное мнение о том, что целая область знания - теоретическая акустика - завершила свое развитие как раздел физики. Дело в том, что, как полагают, с помощью волнового уравнения (а это основной инструмент данной области знания) можно описать любые явления в акустике. На основании этого был сделан вывод, что как теоретическая акустика, так и ее основная практическая ветвь - сейсморазведка, как бы перешли в компетенцию математики.

Но зачем, казалось бы, мне, радиоинженеру, имеющему достаточный опыт работы в схемотехнике, эта информация? Однако Случаю было угодно, чтобы в 1973 году мне пришлось заменить основного преподавателя шахтной геофизики, доцента Ленинградского горного института (ЛГИ), которого внезапно отправили в Москву на 6 месяцев, на повышение квалификации.

Рассуждать было некогда, семестр уже начинался, и после краткого инструктажа этого самого доцента я, обложившись всей существующей литературой, кинулся в этот омут, из которого мне не было суждено вынырнуть.

Любая геофизика, в том числе, и шахтная - на 90% сейсморазведка. Если открыть любой геофизический сборник или материалы какой-нибудь конференции - все сплошь сейсморазведка. Более того, примерно то же соотношение и в денежном соотношении: все страны, позволяющие себе роскошь содержать собственную геофизику, тратят на сейсморазведку более 90% всех геофизических денег. Так что и мне пришлось штудировать главным образом именно эту область знания.

Впрочем, эта область знания оказалась весьма специфической. Прежде всего, отсутствием соответствующих лабораторных работ. Их не было ни в наследстве, оставленном мне покинувшим нас штатным преподавателем, ни, как ни странно, на кафедре геофизики ЛГИ. Так что если по электроразведке, магниторазведке, радиоактивным методам и т.д. мы на лекциях анализировали задачи, смоделированные в лаборатории, то по сейсморазведке все ограничивалось моим говорением и трехэтажными формулами.

Это шло вразрез с моим радиотехническим воспитанием. Для радиофизиков ведь существует только один авторитетный человек, да и тот осциллограф. А если в слово геофизика вторая и бóльшая его составляющая попала не случайно, то каждое ее утверждение должно наглядно иллюстрироваться реально существующим эффектом.

Идея сейсморазведки действительно элементарно проста. Именно поэтому она была описана Пуассоном в начале XIX века, еще за 100 лет до проведения первых практических измерений. Волновое уравнение, написанное им, позволило выйти на описание различных типов упругих волн. Но ведь для того, чтобы иметь отношение к физике, математическое уравнение, какое бы оно ни было красивое, должно содержать аргументы, которые могут быть определяемы в эксперименте. В данном случае, к сожалению, это оказалось не так. Аргументами в волновом уравнении, описывающем поле упругих колебаний, являются параметры движения колеблющихся частиц и/или давление в упругой волне. Ни то, ни другое определить в эксперименте даже на сегодняшний день нельзя, так как в Палате Мер и Весов не существует эталонов и соответствующих датчиков этих субстанций. А следовательно, к полю упругих колебаний как физической реалии волновое уравнение просто не имеет отношения.

Вообще говоря, проблема датчика является в физике ключевой. Нет датчика - нет и научной проблемы. Мы будем относиться с юмором к экстрасенсам до тех пор, пока не существует датчика биополя. Так что же, акустика находится на уровне науки о биополе? Не совсем. Существующие геофоны, гидрофоны, сейсмоприемники и т.д. действительно не являются датчиками каких бы то ни было базисных параметров поля упругих колебаний, но они являются датчиками наличия либо отсутствия самого акустического сигнала, а также источниками информации о спектре этого сигнала. Как увидим дальше, этого оказалось достаточным для разработки научного подхода при изучении поля упругих колебаний.

Впрочем, как бы то ни было, заявить о неправомерности применения волнового уравнения, используемого для описания поля упругих колебаний, после 150 лет его непрерывного использования - шаг непростой. Но давайте посмотрим с другой стороны. Ведь волновое уравнение имеет бесчисленное количество решений, и выбрать необходимое можно лишь задав соответствующие граничные условия. Однако, не имея соответствующих датчиков, нельзя определить и граничные условия. Таким образом, задавая граничные условия умозрительно, нельзя претендовать на реальность получаемых при решении уравнения результатов.

В электродинамике волновое уравнение также является основным инструментом. Однако там базисные параметры электромагнитного поля определяются в эксперименте на нормальном метрологическом уровне, и это, собственно, и определяет правомерность использования волнового уравнения, а также прогресс электродинамики и уровень ее практического использования.

Но, в конце концов, учитывая эффективность сейсморазведочных методов, может быть, можно снизить требования к ее теоретическому обоснованию? Мы ведь все знаем, что основные заслуги при поисках нефти и газа принадлежат сейсморазведке. Да, в самом деле, сейсморазведка не входит в компетенцию метрологов, но ведь главное-то - практические ее результаты.

Осознав это, я направил свои усилия на создание простых лабораторных установок, с помощью которых можно было бы моделировать принцип сейсморазведки. То есть, проще говоря, принцип акустической локации. Однако и здесь возникли совершенно непредвиденные и нигде почему-то не описанные сложности.

Как оказалось, принцип звуковой локации, легко моделируемый в воздухе и в жидкостях, в твердых средах не работает. Исключение составило очень незначительное число материалов, и в частности, оргстекло. В оргстекле легко наблюдать возникновение акустического импульса при ударном воздействии, а также распространение этого импульса и отражение его от границ, которое действительно происходит по законам геометрической оптики.

Однако в подавляющем большинстве материалов - стекле, керамике, металлах и сплавах, а также в горных породах - ни сам акустический импульс, ни его распространение, а тем более, отражение, увидеть нельзя. При ударном воздействии на объекты из подавляющего большинства твердых материалов возникает не отдельный импульс, а длительный колебательный процесс, и распространяется этот процесс явно не по законам геометрической оптики. Никаких следов отраженного от границ сигнала при этом также не видно.

В принципе, мы, не желая того, получили доказательство того, что в большинстве твердых сред (а главное, что в том числе, в горных породах) принцип звуковой локации не работает. Но распространить этот вывод на всю сейсморазведку мы не могли опять же в силу ее представительности. В самом деле, не могла же на пустом методе возникнуть огромная, востребованная во всем Мире область знания.

Однако как бы там ни было, читать курс при отсутствии уверенности в существовании читаемого объекта было нельзя. Я было уж принял решение отказаться от чтения этого курса, поставив себе диагноз "профнепригодность". Но вдруг, в начале 1977 года я получил предложение принять участие в натурных сейсмоизмерениях в условиях угольных шахт. Для этого была подготовлена измерительная аппаратура, позволяющая определять частотный спектр сейсмосигнала.

Как известно, сейсмосигналы, принимаемые сейсмоприемниками при сейсмоизмерениях, имеют вид длительного колебательного процесса неоправданно большой амплитуды. Согласно утверждению ученых-сейсморазведчиков, такого рода сигналы возникают в результате интерференции между множеством элементарных отражений зондирующего импульса от залегающих в земной толще мелких границ. Этот, так называемый, паразитный звон является объектом, с которым борется сейсморазведка в течение всего времени своего существования.

У сейсморазведчиков есть надежда, что если бы удалось уменьшить его амплитуду, то удалось бы, наконец, увидеть на сейсмограммах сам эхо-сигнал. Так вот, как оказалось в результате уже самого первого нашего шахтного измерения, что надежда эта напрасна, но зато спектр этого самого "паразитного звона" однозначно связан с геологическим разрезом в зоне измерений. Дело в том, что, как оказалось, сейсмосигнал, возникающий при ударном воздействии на горный массив, имеет вид не каких-то произвольных по форме и спектру колебаний, а представляет собой одну или несколько затухающих синусоид. При этом частота f_0i каждой из этих составляющих имеет величину, связанную с толщиной (или, как говорят геологи, мощностью) h_i породного слоя следующим выражением:

f_0i = 2500/h_i [(м/с)/м = Гц] (1)

Какой физической реалии соответствует числитель выражения (1), имеющий размерность скорости, тогда было еще неясно, но, выявленное чисто эмпирически, это соотношение выполняется с погрешностью, не превышающей 10% для всего спектра пород угленосной толщи - от слабого аргиллита и до прочнейшего песчаника и известняка при численном равенстве числителя 2500 м/с.

Из этой случайной находки следовало три вывода. Первый заключался в том, что, используя выражение (1), то есть, иначе говоря, спектрально-сейсморазведочный подход, можно без бурения получать информацию о мощностях пород, залегающих как в кровле, так и в почве подземной выработки. Эта информация имеет крайне важное для шахтеров значение, в связи с чем немедленно началась разработка соответствующей аппаратуры. Аппаратура эта впоследствии получила название "Резонанс", и использовалась для оценки и прогнозирования устойчивости пород кровли во всех угольных регионах СССР.

Второй вывод заключался в том, что колебательный процесс, возникающий при ударном воздействии на горный массив, не является мешающим, поскольку содержит информацию о его геологическом строении. Этот вывод накладывал определенные требования на аппаратуру, которые заключаются в том, что она не должна ни в малейшей степени искажать спектр сигнала. Требование это никогда раньше перед сейсмоаппаратурой не ставилось, и выполнение его потребовало весьма нетривиальных решений.

Третий вывод, самый важный для судьбы нового, родившегося при этом направления, в дальнейшем получившего название спектральной сейсморазведки, состоял в том, что породные слои проявляют свойства каких-то новых, неизвестных ранее колебательных систем.

Здесь представляется необходимым дать некоторые пояснения.

Дело в том, что если реакция некоторого устройства (будем говорить, "черного ящика") на короткое (ударное) воздействие имеет вид затухающего синусоидального (гармонического) процесса, значит, этот черный ящик - не что иное как колебательная система. Другого пути, чтобы импульс преобразовать в затухающую синусоиду, просто не существует. Синусоида - это один член ряда Фурье, неделимый информационный кирпичик, который нельзя получить никакой интерференцией. Но в том-то и штука, что единственный мыслимый в акустике процесс, освещенный прошлыми и нынешними авторитетами, с помощью которого предполагается возможным изменение формы сигнала - это интерференция.

В самом деле, а что еще может быть? Сигнал распространяется, многократно отражается, и все эти элементарные отражения векторно складываются друг с другом, то есть, интерферируют. А поскольку другие процессы, способные преобразовывать форму сигнала, неизвестны, то всяческое упоминание о возникновении гармонических сигналов в акустике и сейсмике просто запрещено.

Между тем, наличие такого рода сигналов известно всем. Более того, от них просто деваться некуда. Но называют их квазигармоническими, что само по себе ничего не меняет¹, но зато как бы дает право настаивать на том, что они являются результатом интерференции.

Надо сказать, что здесь мы встретились с удивительным совпадением. Эта история практически полностью повторяет ту, что происходила в XIX веке при открытии электрического колебательного контура.

Первый колебательный контур был случайно реализован в 40-х годах XIX века Джозефом Генри (тем самым, чье имя носит единица индуктивности). Произошло это при исследовании процессов, возникающих при коротком замыкании конденсатора. Это было время, когда начались исследования новой субстанции - электрической жидкости, содержащейся в только что изобретенных гальванических элементах. Эксперимент заключался в том, что заряжался конденсатор (как тогда говорили, "лейденская банка") от гальванического элемента, а для регистрации процесса разряда Генри использовал праобраз амперметра - магнитную стрелку, многократно обвитую проводом. Провод был достаточно толстым, чтобы можно было не считаться с его сопротивлением. На этом основании Дж. Генри полагал, что разряд шел накоротко.

К его величайшему удивлению, стрелка при разряде многократно изменяла направление своего отклонения. Истолковано это было так, что электрическая жидкость при коротком замыкании лейденской банки не только вытекает из нее, но и втекает обратно.

Сначала эта публикация вызвала бурю негодования у всех действующих тогда физиков. Однако после того как оказалось, что описанный результат устойчив при повторении эксперимента, ученые нашли ему объяснение. Многократное изменение направления тока через конденсатор при коротком замыкании было воспринято как следствие интерференционных процессов, возникающих в "электрической жидкости", заполняющей лейденскую банку, в результате ее встряхивания, которому эквивалентно короткое замыкание. В таком виде это явление и существовало в учебниках и научных публикациях еще лет 30.

Второе открытие колебательного контура было сделано спустя 30 лет после этого лордом Кельвином. Он заинтересовался формой сигнала, возникающего при разряде конденсатора и, чтобы удовлетворить свое любопытство, изобрел осциллограф. Увидев же, что электрический ток, протекающий через лейденскую банку, имеет форму синусоиды, Кельвин сообразил, что имеет дело с неизвестной ранее колебательной системой.

И только еще через почти 10 лет электрический LC контур был открыт окончательно, когда Фергюсон осознал роль индуктивности².

Проводя параллель с историей открытия электрического контура, можно сказать, что, найдя зависимость (1), я выполнил только первую часть - обнаружил наличие акустической колебательной системы в виде плоскопараллельной структуры (как частный случай). Однако при этом остался непонятен механизм преобразования импульса в гармонический сигнал, а также был неясен физический смысл числителя выражения (1).

Достаточно долгое время, уже используя на практике выражение (1) и аппаратуру "Резонанс", я, тем не менее, мог без труда доказать, что обнаруженный эффект существовать не может. В самом деле, при условии, что материал пластины однороден по вещественному составу и по акустическим свойствам, можно представить себе лишь один механизм - это прямолинейное распространение упругих колебаний внутри пластины и отражение их от границ. Результат многократного переотражения от поверхностей пластин короткого импульса - это отнюдь не гармонический процесс. В отличие от гармонического, такой процесс имеет очень широкий частотный спектр, и перепутать их невозможно.

Но однажды истину, изложенную в предыдущем абзаце, я воспринял иначе. Реакция на импульсное воздействие имеет вид гармонического сигнала, и это достоверно и однозначно доказывается средствами электроизмерений. Однородность вещественного состава материала пластины, по-видимому, тоже нет оснований подвергать сомнению. Следовательно, раз уж преобразование удара в гармонический процесс все-таки происходит, то должна же быть какая-то неоднородность... А что там у нас с однородностью акустических свойств материала пластины? А может ли оказаться скорость распространения упругих волн неодинаковой в различных точках объекта из однородного по вещественному составу материала?

На чувственном, интуитивном уровне этот вопрос воспринимается с трудом. В самом деле, уверенность в постоянстве скорости звука в однородных по вещественному составу средах, я думаю, рождается вместе с нами. Так же точно, как и некоторые другие аксиомы. Такие, как, скажем, утверждение о том, что параллельные линии не пересекаются в пространстве. Но, с другой стороны, нет такой аксиомы, которая не требовала бы проверки. Ведь, как сказал Лобачевский, аксиома - это не то, что не требует доказательства, а то, что никак не доказать (или не опровергнуть). Чем это кончилось, я имею в виду утверждение о непересекающихся параллельных, известно. Всего лишь, созданием нового типа геометрии.

Здесь я хотел бы немного отвлечься, чтобы показать, что все, что произошло дальше, ничуть от меня не зависело. В самом деле, казалось бы, если уж я получил инструмент для прогнозирования устойчивости кровли в угольных шахтах, то так ли обязательно было доискиваться до механизма того эффекта, на котором этот инструмент работает?.. Я ведь сам только что говорил, что физический эффект совсем не обязательно нужно понимать, чтобы его использовать... Но смотрите сами, ведь аппаратура "Резонанс" была предназначена для сохранения человеческих жизней в условиях шахт. Возможно ли использование в этих целях прибора, который работает на эффекте, которого в принципе быть не может? А если все те результаты, которые мы получали до этого, были результатом какого-то странного стечения обстоятельств, а в дальнейшем, когда использование прибора узаконится, таких обстоятельств больше не будет (или, что еще хуже, они не всегда будут), то наши рекомендации будут способствовать гибели людей, так ведь?

Когда я это осознал, то принял для себя решение аппаратуру шахтерам не давать до тех пор, пока не разберусь в физике используемых эффектов. Мое решение вызвало такую бурю негодования, от шахтных геологов и до самого Минуглепрома, что об этом нужно рассказывать отдельно. Но здесь важно то, что только тот стресс, в котором я оказался, помог мне пройти весь дальнейший путь поисков механизма эффекта преобразования ударного воздействия в гармонический отклик. Не даром у нас потом родился афоризм, что для того, чтобы в голову пришло что-то приличное, надо, чтобы по ней ударили. Вот гипотеза о непостоянстве скорости звука в однородных средах и возникла как результат удара по голове.

Способ проверки факта постоянства скорости звука в однородных средах оказался на удивление простым. Напомню только, что скорость движения какого-либо объекта V прямому измерению не подлежит. Она вычисляется делением отрезка пути r на время t, в течение которого пройден этот путь. Поэтому определяемая в эксперименте скорость всегда является средней, усредненной по отрезку пути r.

Эксперимент, направленный на проверку постоянства скорости звука в однородных по вещественному составу средах, имел следующую логику. Если это постоянство действительно имеет место, то при сквозном прозвучивании пластин величина определяемой скорости распространения упругих волн V не должна зависеть от толщины пластины h. При всей прозрачности этой логики, все же, первый цикл измерений зависимости V(h) был осуществлен на пластинах из оргстекла. Почему это было сделано. Дело в том, что измерение скорости звука в акустике твердых сред является очень серьезной проблемой. При всей кажущейся очевидности и простоте вопроса, результаты реальных измерений в простейших условиях порою настолько непонятны, что теоретикам показалось проще создать массу запретов, чем разобраться в этих неясностях. Так, если результаты ваших измерений не соответствуют каким-то существующим мысленным моделям, вам просто объяснят, что вы не имели права так измерять. Причем эти запреты настолько нечеткие, что в принципе, можно запретить любые измерения. Однако если мы берем два совершенно идентичных по своей геометрии образца из различных материалов, то если вас устроят результаты измерений на одном из них, то запрет точно таких же измерений на другом уже не будет убедительным.

График зависимости скорости распространения упругих колебаний от толщины прозвучиваемых пластин из оргстекла, показанный на рисунке (график 1), свидетельствует о том, что скорость распространения упругих колебаний в оргстекле действительно одинакова во всех точках этого однородного материала. Утолщение линии этого графика при уменьшении толщины пластины соответствует увеличению относительной погрешности определения скорости с уменьшением величины t. Итак, метрологическая корректность при проведении этих измерений может считаться приемлемой.

При точно таком же исследовании пластин из любого металла или сплава, керамики, стекла или горной породы зависимость V(h), как оказалось, имеет вид, подобный графику 2. Как истолковать такой результат?..

 

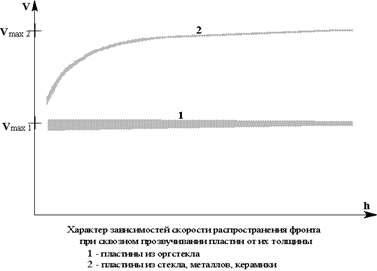
В принципе, подобная зависимость имела бы место, если бы мы таким же точно способом определяли скорость движения автомобиля при изменении расстояния между точками его начала движения и остановки. Средняя или крейсерская скорость любого средства передвижения уменьшается при уменьшении длины пути за счет неизбежного присутствия участков, где скорость сначала плавно увеличивается, а затем, перед остановкой плавно уменьшается.

Однако применительно к упругой волне, распространяющейся в однородном материале пластины, подобная модель была непредставима. Честно говоря, этот эксперимент готовился мною исключительно для того, чтобы раз и навсегда исключить даже сами мысли о возможности неодинаковости скорости в различных точках внутри объектов из однородной среды.

Вот уж никогда не думал, чтобы рядовое, в общем-то, измерение могло подействовать на меня столь эмоционально... Настолько подействовало, что когда аппаратура уже была готова для осуществления измерений, то я понял, что я сделать эти исследования не могу, и отложил их на следующий день.

Более того, результаты этого эксперимента сильнейшим и неожиданным образом подействовали на всех окружающих людей, так или иначе причастных к нашим работам. Некоторые ближайшие коллеги, с участием которых проводились первые измерения зависимости V(h), вдруг стали отказываться от своего в них участия, а родная кафедра внезапно повела курс на уничтожение лаборатории вместе с тем курсом, который я читал.

Впрочем, я тогда ничего вокруг не замечал, одержимый постановкой такого высокоточного измерения, которое могло бы закрыть это уж точно ошибочное, никому не нужное открытие. Однако чем изысканнее были исследования, тем яснее вырисовывалась картина. Да, действительно, звуковая волна, проникая в пластину из подавляющего большинства твердых сред, сначала разгонялась, а затем, при приближении ко второй границе плавно замедлялась. И вот тогда мне стало плохо по-настоящему.

Если многочисленные болельщики мучили меня вопросом, почему в оргстекле, в отличие от стекла, этот эффект отсутствует, то меня самого не отпускала другая, совершенно мистическая проблема:

откуда упругая волна знает, что приближается граница,

и что пора начать замедление своего движения?

Вот где было сумасшествие! Этот вопрос горел в моем замутненном сознании с настойчивостью маньяка, не отпуская ни на минуту... Вот уже более 20 лет прошло с тех пор, но этого состояния непрерывной и полной огорошенности забыть нельзя.

Ну, что тут скажешь, невольно начнешь верить в Провидение. Не знаю, чьей волей, но в руках у меня оказалась книга о жизни Ньютона, откуда я узнал, что с ним происходила примерно такая же история. При обсуждении закона всемирного тяготения его оппоненты, да и он сам были одержимы подобным же вопросом: где та "веревка", что заставляет взаимодействовать между собой планеты и прочие объекты? Так же, как и меня, его эта мука не отпускала года два. После чего его осенило, что закон должен отвечать не на вопрос "почему", а исключительно на вопрос "как"! В конце концов, если при метрологически корректном измерении эффект повторяем, значит, его нужно учитывать, с ним нужно считаться независимо от нашего понимания. Разве мало мы используем эффектов, не понимая их физики? Да хоть бы тот же закон всемирного тяготения...

И все, больше никаких мук. Принимаем как данность, что в подавляющем большинстве твердых сред скорость распространения фронта упругих колебаний снижается при приближении фронта к поверхности объекта. То есть в подавляющем большинстве твердых сред существует приповерхностный слой, толщина которого достигает 2 см, в котором скорость распространения фронта упругих колебаний имеет пониженное значение за счет уменьшения ее с приближением фронта к поверхности.

Отношение к этому эффекту как к доказанному факту позволило обнаружить еще некоторые новые эффекты. Кстати, один из них позволил ответить на тот злополучный вопрос, который я обвел рамочкой. Но наиболее интересным мне кажется эффект акустического резонансного поглощения (АРП). Суть его в следующем.

Если при сквозном прозвучивании пластин из любых материалов изменять частоту генератора, возбуждающего электроакустический преобразователь, то можно увидеть на некоторых частотах так называемый эффект монохроматора, известный в оптике еще как эффект просветления. Эффект этот заключается в том, что, в результате интерференционных (а в данном случае, это действительно так) процессов при многократном переотражении сигнала внутри слоя на некоторых частотах сигнал проходит через пластину целиком при абсолютном отсутствии отражения от нее. Условие эффекта монохроматора заключается в том, что на толщине пластины h должно укладываться целое количество полуволн продольных колебаний или, иначе говоря,

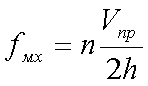 , где (2)

f_мх - частоты, на которых наблюдается эффект монохроматора,

n - любое целое число,

V_пр - скорость продольных волн.

На других частотах зондирующий сигнал частично отражается от пластины, и за счет этого уменьшается уровень сигнала, который проходит сквозь пластину. Эффект монохроматора можно наблюдать на пластинах из всех твердых сред. Однако при исследовании пластин не из оргстекла, а из других, перечисленных выше материалов, обнаружился еще один эффект, по смыслу диаметрально противоположный эффекту монохроматора. Как оказалось, на некоторых частотах (f_АРП) отсутствует не отражение, а прохождение сигнала через пластину, но при этом не увеличивается отражение от нее. Естественен вопрос: а куда же девается та часть сигнала, которая и не проходит насквозь, но и не идет на увеличение отражения?

И опять год поисков. В результате которых оказалось, что искомая часть сигнала излучается пластиной через ее же собственные торцы. Этот эффект, по аналогии с ферромагнитным, парамагнитным и другими известными в физике эффектами резонансного поглощения, был назван эффектом акустического резонансного поглощения. Переориентация первичного акустического потока в ортогональном направлении есть следствие того, что эффект АРП идет на поперечных волнах.

Условие эффекта АРП следующее:

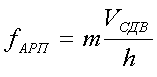 , где (3)

m - любое нечетное число,

V_СДВ - скорость поперечных (сдвиговых) волн.

Низшая частота, на которой наблюдается эффект АРП (при m =1), оказалась равной частоте f₀, которая возникает при ударном возбуждении слоя-резонатора. Отсюда и название эффекта, так как совпадение собственной частоты с возбуждающей - это и есть резонанс. Таким образом, числитель формулы (1) есть не что иное, как скорость поперечных волн V_СДВ.

Любой новый физический эффект - это бездна информации. Особенно когда это касается такого фундаментального эффекта как АРП. Ограничиваясь рамками настоящего повествования, можем отметить, что:

Слои из большинства твердых сред являются резонаторами, то есть при ударном воздействии они откликаются гармоническим затухающим процессом на частоте, равной f₀.

Собственный колебательный процесс идет на поперечных волнах, и поэтому реализация эффекта АРП может считаться первым метрологически корректным способом определения скорости поперечных волн.

Наличие приповерхностных зон, в которых скорость распространения упругих волн не является постоянной, а уменьшается с приближением к границе, является условием существования резонатора. Мы научились уничтожать эти зоны, и тогда стеклянные, металлические и т.п. пластины перестают быть резонаторами. Мы научились создавать эти зоны, и тогда пластины из оргстекла, жидкостные и газовые слои становятся слоями-резонаторами.

Слой-резонатор - это частный случай. Резонатором является объект любой формы при наличии приповерхностных слоев с непостоянной скоростью звука, но при этом количество собственных частот колебательного процесса, возникающего в этом объектах, равно количеству его размеров. К примеру, параллелепипед имеет три размера и, соответственно, три частоты его собственного звучания.

Определяя с помощью спектрально-акустических измерений спектр собственного звучания, нетрудно определить размеры объекта, а также выявить скрытые границы, в частности, обусловленные дефектами материала. И этот факт породил спектрально-акустическую дефектоскопию.

Границы, выявляемые при спектрально-акустических измерениях, представляют собой поверхности, по которым возможно взаимное проскальзывание соседних сред. Это определяется тем, что формируются собственные колебания на поперечных волнах.

Понятно, что до тех пор, пока не будет создан формально-математический аппарат для описания преобразования импульсного воздействия в гармонический отклик наподобие того, как это было сделано Кельвином для электрического колебательного контура, открытие акустической колебательной системы нельзя считать завершенным. И, вместе с тем, мы не только имеем право объявить о рождении новой, неведомой ранее колебательной системы, но, и обязаны это сделать, так как практическое значение этого факта просто огромно. На базе этого нового знания создана спектральная сейсморазведка, на счету которой уже есть несколько новых месторождений полезных ископаемых. Кроме того, с помощью спектральной сейсморазведки оказалось возможным впервые, за всю историю строительной науки оценивать и прогнозировать надежность инженерных сооружений. Метод спектрально-сейсморазведочного профилирования (ССП) позволяет еще до начала строительства дома показать, где в будущем доме начнут развиваться трещины, и как передвинуть строительную площадку, чтобы этих трещин не было. Я не ставлю своей задачей перечислять все возможности этого метода, а заинтересовавшимся можно заглянуть на сайт http://www.newgeophys.spb.ru/, где, кроме примеров использования метода ССП, опубликована книга по основам спектрально-акустического направления в физике. Сейчас же, когда спектральная сейсморазведка показала свою жизнеспособность, возникла необходимость найти точки соприкосновения нового метода с уже существующими, традиционными сейсмометодами.

При поисках этих точек соприкосновения мне необходимо было очертить реальные возможности также

Поделиться:

Воспользуйтесь поиском по сайту: