Методические указания по изучению дисциплины

Дисциплина «Механика» изучается курсантами УВАУ ГА(и) на завершающем этапе общетехнической подготовки; опирается на знания, полученные ими по дисциплинам естественно-научного цикла («Математика», «Физика», «Химия» и др.), а также по дисциплинам общетехнической предметной подготовки («Начертательная геометрия», «Инженерная графика», «Материаловедение», «Технология конструкционных материалов», «Метрология, стандартизация и сертификация» и др.)

Цель изучения дисциплины – формирование у обучаемых основ инженерно-технического мышления и общетехнической культуры. Знание данной дисциплины позволит квалифицированно эксплуатировать механическое оборудование гражданской авиации.

Основными задачами изучения дисциплины являются:

- изучение основных типов конструкций (деталей, узлов, механических передач, соединений деталей);

- усвоение базовых принципов конструирования;

- овладение навыками расчетов конструкций и их элементов.

Курсант, изучивший дисциплину, должен

знать:

- основные законы равновесия и их приложение в технике;

- типы и законы движения простейших механических систем с кинематическими характеристиками под действием изменяющихся по времени и направлению систем сил;

- методы расчета на прочность и жесткость конструкций и узлов.

уметь:

- определять кинематические параметры, характеризующие движение системы;

- использовать основные теоремы (законы) механики при изучении специальных дисциплин;

- выполнять расчет на прочность и жесткость простейших элементов механических конструкций;

владеть навыками использования полученных знаний и умений в будущей профессиональной деятельности.

Курс «Механика» состоит из четырех разделов: «Теоретическая механика», «Сопротивление материалов», «Теория механизмов» и «Детали машин и основы конструирования».

Обучение курсантов осуществляется путем изложения на лекционных занятиях теоретических основ дисциплины, закрепления теоретических знаний на лабораторно-практических занятиях и в процессе самостоятельной работы курсантов при изучении рекомендуемой литературы и приобретения практических навыков решения задач на практических занятиях под руководством преподавателя, в процессе самостоятельного выполнения расчетно-графических работ.

Выполненные самостоятельно лабораторно-практические работы защищаются курсантами в форме ответов на вопросы преподавателя. Предусматривается написание контрольных работ (по материалам к контрольным работам) и тестирование по каждой теме дисциплины по тестам для контроля текущей успеваемости курсантов.

Итоговый контроль осуществляется в форме устного экзамена по разработанным билетам либо в виде зачета. К экзамену допускаются курсанты, прослушавшие курс лекций по дисциплине, выполнившие и защитившие все лабораторно-практические работы, написавшие на положительные оценки контрольные работы, успешно прошедшие текущее тестирование по дисциплине. В качестве поощрения допускается освобождение от сдачи экзамена курсантов, успешно (досрочно и в срок) сдавших и защитивших все лабораторно-практические работы и получивших положительные оценки по результатам текущей успеваемости. Оценка за экзамен в этом случае определяется по результатам текущей успеваемости, учитывающей результаты сдачи лабораторно-практических работ, оценки по контрольным работам и оценки промежуточного тестирования при изучении дисциплины.

Зачет проводится по прикладной части «Механики» в третьем и четвертом семестрах. К зачету допускаются курсанты, выполнившие предусмотренные учебной программой лабораторно-практические работы и защитившие их. Зачет проводится в форме контрольной работы, предусматривающей решение задач и тестирование.

Содержание каждого из разделов подробно изложено в учебной программе по дисциплине. При изучении теоретической части курса недостаточно ограничиваться только конспектом. Обязательным условием успешного усвоения материала является изучение соответствующих тем по рекомендуемой литературе.

Необходимо к каждой лекции или лабораторно-практическому занятию курсантам изучить и повторить материал предыдущего занятия или лекции. Только при этом условии может быть достигнута непрерывность и последовательность изучения предмета, обеспечивающих наиболее полное и твердое усвоение основных принципов и методов расчета.

Лабораторно-практические работы по «Механике» составлены в соответствии с теоретическим курсом и являются его неотъемлемым дополнением. Целью этих работ является закрепление и углубление теоретических знаний, полученных на лекциях, и развитие навыков самостоятельного применения этих знаний при расчетах. В методических указаниях к каждой работе даются основные теоретические сведения, необходимые для понимания изучаемых вопросов, описание оборудования, цель и задачи работы, порядок ее выполнения. Приводятся требования к оформлению отчета, а также контрольные вопросы, ответы на которые способствуют более глубокому освоению и закреплению изучаемого материала.

Предварительная подготовка курсанта к выполнению лабораторно-практической работы заключается в глубоком изучении теоретического материала по конспекту или учебнику и по данному учебному пособию. По каждой работе оформляется индивидуальный отчет. Все графические построения выполняются карандашом с помощью чертежных инструментов. По каждой выполненной работе курсант должен отчитаться на лабораторно-практическом занятии или на консультации.

При изучении дисциплины «Механика» большое место занимают проблемы специализации, решаемые установлением тесных связей с профилирующими кафедрами. Одним из путей специализации является включение в индивидуальные домашние задания задач, непосредственно связанных со специальностью. Это способствует установлению надежных межпредметных связей. Такое взаимопроникновение учебных дисциплин нацеливает будущих специалистов на комплексное применение знаний, умений и навыков.

УЧЕБНОЕ ПОСОБИЕ

Теоретическая механика

Статика

Тема 1. Основные понятия и аксиомы статики

Материальная точка – тело, размерами которого можно пренебречь. Она обладает массой и способностью взаимодействовать с другими материальными точками. Например, в небесной механике планеты, движущиеся вокруг Солнца, часто рассматривают как материальные точки, поскольку их размеры малы по сравнению с размерами орбит. Пользоваться понятием материальной точки целесообразно также и в том случае, когда все частицы движущегося физического тела перемещаются одинаково.

Совокупность материальных точек, положения и движения которых взаимосвязаны между собой, называется системой материальных точек.

В теоретической механике пренебрегают малыми деформациями тел и считают эти тела абсолютно твердыми.

Силой называется количественная мера механического взаимодействия тел. Сила является векторной величиной, действие силы на тело определяется численным значением (модулем), направлением и точкой приложения силы (рис. 3.1.1).

Рис. 3.1.1

На схемах сила изображается направленным отрезком. Основной единицей измерения силы является 1 Ньютон (1 Н).

Совокупность нескольких сил, действующих на тело, называется системой сил.

Эквивалентная система сил – система сил, оказывающих одинаковое механическое действие на одно и то же тело.

Уравновешенная система сил – система сил, под действием которых тело находится в равновесии.

Сила, эквивалентная некоторой системе сил, называется равнодействующей.

Сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону, называется уравновешивающей силой.

Внешними силами называются силы, действующие на тело со стороны других тел.

Внутренние силы – силы взаимодействия между частицами одного и того же тела.

В статике рассматриваются условия равновесия внешних сил.

Аксиомы статики. В основе статики лежат несколько не требующих доказательства аксиом, из которых выводятся все теоремы и уравнения.

Аксиома 1. Две силы, действующие на абсолютно твердое тело, уравновешиваются только тогда, когда они равны по величине и направлены по одной прямой в противоположные стороны (рис. 3.1.2).

Рис. 3.1.2

Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изменится, если прибавить к ней или отнять от нее уравновешенную систему сил () ≡(), т.к. () ≡ 0 (рис. 3.1.3).

Рис. 3.1.3

Следствие из аксиомы 1 и 2. Действие силы на абсолютно твердое тело (АТТ) не изменится, если точку приложения этой силы перенести по линии ее действия. Пусть на тело в точке А действует сила 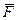(рис. 3.1.4). Добавим в точке В, выбранной произвольно на линии действия силы 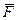, уравновешенную систему сил и равных по абсолютной величине 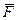и направленных по линии ее действия. На основании аксиомы 1 силы 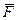и будут уравновешены и их можно отбросить (аксиома 2). В результате получим силу , но приложенную не в точке А, а в точке В. Отсюда следует, что сила, приложенная к АТТ, есть вектор скользящий.

Рис. 3.1.4

Аксиома 3. Равнодействующая двух сил, приложенных к АТТ в одной точке, равна их геометрической сумме , т.е. выражается по модулю и направлению диагональю параллелограмма, построенного на этих силах (рис. 3.1.5):

. (3.1.1)

Рис. 3.1.5

Аксиома 4. Всякому действию одного тела на другое соответствует равное по величине, но противоположное по направлению противодействие. Действие и противодействие – это силы, приложенные к двум различным телам, поэтому они не уравновешиваются (рис. 3.1.6).

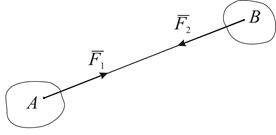
Рис. 3.1.6

Аксиома 5. Если деформируемое тело под действием системы сил находится в равновесии, то при отвердевании его равновесие сохраняется.

Под действием сил тело D находится в равновесии. Если трос CB заменить стержнем, то равновесие не нарушится, равновесие не нарушится и в том случае, если трос BD заменить стержнем, если же стержень АВ заменить тросом – равновесие нарушится (рис. 3.1.7).

Связи и их реакции. Твердое тело называется свободным, если оно может перемещаться в пространстве в любом направлении (ВС в полете). Тело, ограничивающее свободу движения данного твердого тела, является по отношению к нему связью. Твердое тело, свобода движения которого ограничена связями, называется несвободным (самолет на ВПП).

Сила, с которой связь действует на тело, препятствуя его перемещению в том или ином направлении, называется силой реакции этой связи.

Для нахождения реакции связей используют аксиому связей, на основании которой всякое несвободное тело можно рассматривать как свободное, если отбросить связи, заменив их действие на тело силами реакций этих связей.

Направление силы реакции связи противоположно тому направлению, в котором активные силы стремятся переместить тело.

Различают три группы связей:

1. Гибкие связи (трос, цепь, ремень, канат): реакции связей направлены по оси связей (рис. 3.1.8).

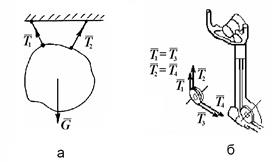
Рис. 3.1.8

Если нить отклоняется роликом, в котором не учитывается трение, то натяжение нити не изменяется. Например, натяжение тросов, идущих от штурвала к элеронам ВС, с обеих сторон равны по модулю | Т ₁| = | Т ₃|, |Т ₂ |= | Т ₄| (рис. 3.1.8, б).

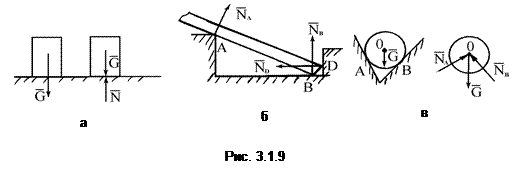2. Твердые, идеально гладкие связи: реакция направлена по общей нормали к поверхностям соприкасающихся тел (рис. 3.1.9).

3. Шарнирные связи. Шарниром в механике называется устройство, допускающее поворот одного тела относительно другого, но ограничивающее при этом линейные перемещения этих тел. Шарнирами, например, являются соединения А, В, С элементов задней опоры самолета (рис. 3.1.10), узлы А, В, С, D подвески авиационного двигателя (рис. 3.1.11).

Реакция цилиндрического шарнира 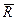может иметь любое направление в плоскости, перпендикулярной оси шарнира. Направление реакции зависит от величины и направления действующих на тело сил. Реакция подвижного шарнира всегда направлена по нормали к опорной поверхности шарнира (рис. 3.1.12, б, в).

Рис. 3.1.12

Шаровой шарнир исключает любое перемещение тела во всех направлениях, кроме вращения, поэтому реакция шарового шарнира может иметь любое направление в пространстве. Чаще всего эту реакцию представляют в виде трех ее составляющих по осям координат x, y, z (рис. 3.1.13).

Разнообразные опорные устройства валов машин схематически представляют подшипниками двух типов: радиальным (цилиндрическим – А), не препятствующим некоторым осевым смещениям вала, и радиально-упорным (В), исключающим осевые перемещения вала (рис. 3.1.14).

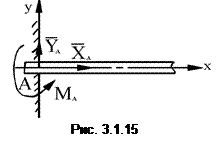Неподвижная защемляющая опора или жесткая заделка. На заделанный конец балки со стороны опоры действует система распределенных сил, которую заменяем эквивалентной системой сосредоточенных сил и моментом М _А, приложенных в точке А (рис. 3.1.15).

Тема 2. Система сходящихся сил

Сложение сходящихся сил. Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил.

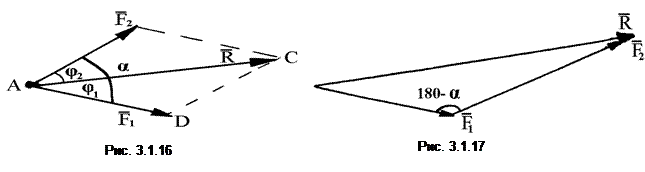
Сложить две или несколько сил – значит заменить эти силы одной силой, им эквивалентной, т.е. найти их равнодействующую (рис. 3.1.16).

Из ∆ ADC: т.к. cos(180 – a) = –cosa,то получим

, (3.1.2)

. (3.1.3)

Найти равнодействующую можно также, построив половину параллелограмма – треугольник сил, в котором равнодействующая является замыкающей стороной (рис. 3.1.17).

Равнодействующая трех сил, приложенных в одной точке и не лежащих в одной плоскости, равна по модулю и направлению диагонали параллелепипеда, построенного на этих трех силах (рис. 3.1.18).

Так как , а , то .

Равнодействующая нескольких сходящихся сил выражается по модулю и направлению вектором, соединяющим начальную и конечную точки ломаной линии (правило силового многоугольника) (рис. 3.1.19).

или . (3.1.4)

Сходящиеся силы уравновешиваются в случае, если их равнодействующая равна нулю, т.е. многоугольник сил замкнут. Конец вектора последней силы совпадает с началом вектора первой силы, все силы направлены по контуру многоугольника в одну сторону, т.е. .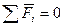

Согласно, аналитическому условию равновесия при R = 0 получим

,

где ∑ F_ix, ∑ F_iy, ∑ F_iz – проекции сил на координатные оси. Следовательно,

∑ F_ix = 0; ∑ F_iy = 0; ∑ F_iz = 0. (3.1.5)

Для равновесия тела при действии на него пространственной системы сходящихся сил необходимо и достаточно, чтобы сумма проекций этих сил на каждую из координатных осей была равна нулю.

Теорема о равновесии трех непараллельных сил. Линии действия трех непараллельных взаимно уравновешивающихся сил, лежащих в одной плоскости, пересекаются в одной точке. К твердому телу в точках А ₁, А ₂, А ₃ приложены три непараллельные взаимно уравновешивающиеся силы лежащие в одной плоскости. Перенесем силы и в точку О и найдем их равнодействующую. Сила будучи уравновешивающей системы сил и , равна по модулю их равнодействующей 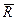и направлена по линии ее действия в противоположную сторону (рис. 3.1.20).

Сходящиеся силы, приложенные к ВС. Часто для качественной оценки сил, действующих на ВС, их представляют в виде сходящихся сил. Равнодействующую сил давления воздушного потока на крыло и сил трения протекающего воздуха о его поверхность можно считать суммой двух сходящихся сил (рис. 3.1.21):

,

где 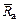– аэродинамическая сила крыла;

– сила лобового сопротивления;

– аэродинамическая подъемная сила крыла.

В виде сходящихся сил представляют часто и силы, действующие на ВС в полете. При наборе высоты, например, в упрощенную систему действующих на ВС сходящихся сил входят (рис. 3.1.22):

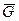– сила тяжести (вес самолета);

– тяга винта (или газотурбинного двигателя);

– сила лобового сопротивления самолета;

– аэродинамическая подъемная сила.

Аналогичным образом упрощают систему сил, действующих на ВС и в других режимах полета.

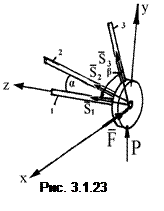
Пример. Ось колеса шасси легкого самолета крепится к фюзеляжу с помощью трех шарнирно закрепленных подкосов (рис. 3.1.23), оси которых пересекаются в точке О. Ось подкоса 1 совпадает с осью колеса, подкос 2 расположен в горизонтальной плоскости под углом a = 30° к оси первого подкоса, а подкос 3 – в вертикальной плоскости под углом b = 60°. На колесо действуют силы Р = 10 кН и F = 3 кН. Определите усилия в подкосах.

Решение. Рассмотрим равновесие колеса. На колесо действуют две активные силы ( и 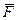) и наложены связи – невесомые стержни 1, 2, 3. Используя аксиому освобождаемости от связей, мысленно отбрасываем связи, заменяя их действие реакциями . Выбираем оси координат так, чтобы решение задачи было наиболее простым. Составляем условия равновесия колеса, находящегося под действием пространственной системы сходящихся сил :

∑ F_ix =0; – F – S ₂ sin a = 0; S ₂ = – 6 кН.

∑ F_iy =0; P + S ₃ sin b = 0; S ₃ = – 11,5 кН.

∑ F_iz =0; S ₁ + S ₂ cos a + S ₃ cos b = 0; S ₁ = 11 кН.

Освобождая тело от связей, мы полагали все стержни растянутыми. Знак «минус» в полученных значениях реакций S₂ и S₃ означает, что в действительности они сжаты.

Тема 3. Теория пар сил

Момент силы относительно центра. Опыт показывает, что эффект действия силы, приложенной к телу (например, к рычагу, штурвалу), на разных расстояниях от точки закрепления тела, зависит от так называемого момента силы относительно точки закрепления.

Моментом силы 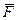относительно центра О называется произведение модуля силы на кратчайшее расстояние от центра О до линии действия силы:

M ₀(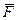) = ± Fh, (3.1.6)

где h – кратчайшее расстояние от центра О до линии действия силы .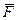

Момент силы считается положительным, если сила стремится повернуть тело вокруг центра О против хода часовой стрелки и отрицательным, если по ходу часовой стрелки (рис. 3.1.24, 3.1.25). Момент силы измеряется в Н·м.

Момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия. Момент силы относительно центра О равен нулю, если сила равна нулю или, если линия действия силы проходит через центр О (плечо равно нулю).

Графически абсолютная величина момента силы относительно центра О выражается удвоенной площадью Δ ОАВ:

M ₀ (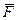) = 2 S ∆ ОАВ. (3.1.7)

Момент силы относительно центра как векторное произведение. Введенного понятия «момент силы относительно центра как алгебраическая величина» оказывается недостаточно в случае сил, произвольно расположенных в пространстве. Плоскости поворота у разных сил будут различными и должны задаваться дополнительно. Удобно ввести понятие «момент силы относительно центра как вектор», модуль которого равен произведению модуля силы на ее плечо, а направление перпендикулярно плоскости, проходящей через линию действия силы и центр момента.

Вектор момента силы прикладывают в центре момента и направляют в сторону, откуда сила видна вращающей тело в направлении, противоположном ходу часовой стрелки (рис. 3.1.26). Соединим центр момента О с точкой приложения силы радиусом-вектором 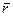и найдем векторное произведение .

По определению векторного произведения

| |= 2 S ×∆ ОАВ.

Модуль вектора момента силы также равен удвоенной площади ∆ ОАВ.

Тогда

= .

Направление векторного произведения также совпадает с направлением вектора момента. Следовательно, вектор-момент силы 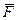относительно центра О можно рассматривать как векторное произведение радиус-вектора 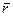, проведенного из этой точки в точку приложения силы, на вектор силы :

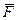(3.1.8)

Момент силы относительно оси. Чтобы охарактеризовать вращательный эффект, создаваемый силой, стремящейся повернуть тело вокруг некоторой оси, вводится понятие «момента силы относительно оси».

Рассмотрим твердое тело, которое может вращаться вокруг оси OZ (рис.3.1.27). Пусть на тело действует сила 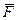, приложенная в точке А. Проведем через точку А плоскость OXY, перпендикулярную оси OZ, и разложим силу 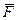на две составляющие: , параллельную оси OZ, и , лежащую в плоскости XY. Составляющая, параллельная оси OZ, крутящего момента не создает, а, следовательно, весь вращательный эффект, создаваемый силой 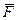,будет вызван ее составляющей _.

M_z (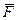) = M ₀ () = ± F_xy h = ± 2 S ∆OAB ₁.(3.1.9)

Моментом силы относительно оси называют момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.

Момент силы относительно оси считается положительным, если смотря навстречу оси Z, можно видеть проекцию F_xy, стремящейся вращать плоскость XY вокруг оси Z в сторону, противоположную вращению часовой стрелки.

Момент силы относительно оси равен нулю:

1) если F_xy = 0, т.е. линия действия силы параллельна оси OZ;

2) если h = 0, т.е. линия действия силы пересекает ось OZ.

Следовательно, если сила и ось лежат в одной плоскости, то момент силы относительно этой оси равен нулю.

Пара сил. Момент пары. Система двух равных по модулю, параллельных и противоположно направленных сил называется парой сил (рис. 3.1.28).

Пара сил не имеет равнодействующей, и силы пары не уравновешиваются. Действие пары на тело характеризуется ее моментом:

1) вектор-момент перпендикулярен плоскости действия пары;

2) направлен в ту сторону, чтобы, смотря с его конца, вращение было происходящим против хода часовой стрелки;

3) величина вектора 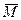равна в выбранном масштабе численному значению момента пары.

Вектор-момент пары равен векторному произведению радиуса-вектора 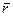на ту из сил пары, к началу которой направлен вектор :

, (3.1.10)

или

, (3.1.11)

по модулю

M = r F sin α = Fh; M = ± Fh. (3.1.12)

Пары сил в пространстве эквивалентны, если их моменты геометрически равны. Геометрическая сумма моментов составляющих пар сил равна моменту эквивалентной им пары:

. (3.1.13)

Пары сил, произвольно расположенные в пространстве, взаимно уравновешиваются в том случае, если геометрическая сумма их моментов равна нулю. Если пары сил расположены в одной плоскости, то моменты этих пар сил, направленные по одной прямой, складываются алгебраически.

Момент пары сил, эквивалентный системе пар сил на плоскости, равен алгебраической сумме моментов составляющих пар (рис. 3.1.29):

, (3.1.14)

где M_i = ± F_i d_i.

Пары сил, расположенные в одной плоскости, взаимно уравновешиваются, если алгебраическая сумма их моментов равна нулю:

= 0.

Силовое воздействие на ВС часто приводится к паре сил. Например, аэродинамические силы (силы сопротивления воздуха вращению) воздушного винта складываются в пару, называемую аэродинамическим (реактивным) моментом винта М _в (рис. 3.1.30). Чем большую мощность развивает двигатель, тем больше реактивный момент, вызывающий крен ВС. Этот момент уравновешивают некоторым отклонением элеронов; аэродинамические силы _Э._пр и _Э.. _лев составляют пару с моментом, равным значению реактивного момента воздушного винта и обратным его направлению.

Тема 4. Система произвольно расположенных сил

Теорема о параллельном переносе силы (теорема Пуансо). Действие силы на АТТ не изменится, если перенести ее параллельно самой себе в некоторую точку (центр приведения) присоединив при этом пару сил. Момент присоединенной пары равен моменту приведенной силы, относительно центра приведения. В точке А (рис. 3.1.31) приложена сила 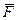, которую необходимо перенести в точку В. Как это сделать? В точке В прикладываем силы, равные по модулю сил ; () ≡ ()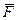; () ≡ 0. Получили эквивалентную систему трех сил, которую можно рассматривать как совокупность силы и пары сил с моментом (рис. 3.1.32).

Пару называют присоединенной; ее момент равен моменту переносимой силы относительно центра приведения и, следовательно, зависит от положения этого центра.

Приведение произвольной пространственной системы сил к данному центру. Главный вектор и главный момент. Систему сил, приложенных к телу, можно упростить, используя теорему о параллельном переносе силы. В результате приведения произвольной пространственной системы сил к данному центру в общем случае получаем главный вектор, равный геометрической сумме всех сил системы, и главный момент, равный геометрической сумме моментов всех приводимых сил относительно центра приведения (рис. 3.1.33).

Сложим и т.д., получим силовой многоугольник, где

. (3.1.15)

Затем векторно сложим векторы моментов:

(3.1.16)

, (3.1.17)

где (x ₁, y ₁, z ₁), (x ₂, y ₂, z ₂) проекции на координатные оси каждой из сил.

Главный вектор инвариантен по отношению к центру приведения. Главный момент зависит от выбора центра приведения.

По модулю главный вектор вычисляется следующим образом:

R * = , (3.1.18)

где

R_x = X ₁ + X ₂ +...+ X_n = ∑ X_i; (3.1.19).

R_y = Y ₁ + Y ₂ +...+ Y_n = ∑ Y_i;

R_z = Z ₁ + Z ₂ +...+ Z _n = = ∑ Z –

проекции главного вектора на координатные оси ^* (R_x, R_y, R_z).

Направление находим по направляющим косинусам:

co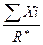s( 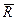^*, ) = ; cos( ^*, ) = ; cos(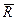 ^*, ) = . (3.1.20)

Главный момент

;

M _{0 x} = ∑ M_x (); M _{0 y} =∑M_y (); M _{0 z} = ∑ M_z (); (3.1.21)

M ₀ = 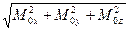. (3.1.22)

Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех этих сил на каждую из координатных осей равнялась нулю и чтобы алгебраическая сумма моментов всех сил системы относительно каждой из трех координатных осей равнялась нулю:

∑ X_i = 0; ∑ Y_i = 0; ∑Z_i = 0;

∑ M_x () = 0; ∑M_y () = 0; ∑ M_z () = 0. (3.1.23)

Система параллельных сил. Если ось OZ параллельна силам, то три уравнения (3.1.23) обращаются в тождества, так как проекции сил на оси OX и OY и их моменты относительно оси OZ равны нулю. Оставшиеся три уравнения являются уравнениями равновесия параллельных сил в пространстве (рис. 3.1.34):

Z_i = 0; ∑ M_x () = 0; ∑M_y () = 0. (3.1.24)

Для параллельных сил, расположенных в плоскости XOY (рис. 3.1.35), имеем два уравнения равновесия:

∑ Y_i = 0; ∑ M ₀() = 0. (3.1.25)

Плоская система произвольно расположенных сил. Если силы действуют в плоскости XOY (рис.3.1.36), то суммы проекций их на ось OZ и моментов относительно осей OX и OY равны нулю.

При равновесии тела под действием плоской системы сил суммы их проекций на оси координат и сумма моментов относительно произвольного центра, лежащего в плоскости сил, равны нулю:

∑ X_i = 0; ∑ Y_i = 0; ∑M ₀() = 0.(3.1.26)

Примеры упрощения системы сил, действующих на ВС. Силы взаимодействия ВС с поверхностью взлетно-посадочной полосы (ВПП) и воздухом при движении по земле и в полете подчиняются сложным закономерностям. Во всех случаях систему сил, действующих на ВС, упрощают. Например, воздушное давление, неравномерно распределенное по нижней и верхней поверхностям крыла (или стабилизатора, киля), часто суммируют и относят к одной поверхности.

Силы, действующие на ВС в горизонтальном полете с постоянной скоростью без бокового ветра, могут быть приведены к плоской системе сил (рис. 3.1.37).

Вес ВС (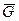), подъемная сила крыла (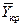) и горизонтального оперения (), тяга двигателей () и сила лобового сопротивления ()удовлетворяют трем уравнениям равновесия:

1. Условие сохранения постоянной скорости:

∑ X_i = 0, P – Q = 0; (3.1.27)

2. Условие сохранения постоянно

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: