 |
Летова Т. А. , Пантелеев А. В. Методы оптимизации. Практический курс, 2011
|
|
|
|
СХОДИМОСТЬ МЕТОДА
Теорема 1. Если квадратичная функция f(x) = (х, Нх) + (b, х) + а с неотрицательно определенной матрицей Н достигает своего минимального значения на Rn, то метод Флетчера-Ривса обеспечивает отыскание точки минимума не более чем за n шагов.
Теорема 2. Пусть функция f(x) дифференцируема и ограничена снизу на Rm, а ее градиент удовлетворяет условию Липшица
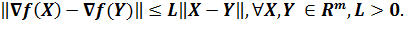
Тогда при произвольной начальной точке 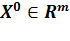 для метода Полака-Рибьера имеем
для метода Полака-Рибьера имеем 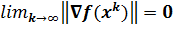 .
.
Теорема 2 гарантирует сходимость последовательности {xk} к стационарной точке x*, где ▽f(x*)=0. Поэтому найденная точка x* нуждается в дополнительном исследовании для ее классификации. Метод Полака-Рибьера гарантирует сходимость последовательности {xk} к точке минимума только для сильно выпуклых функций.
Оценка скорости сходимости получена только для сильно выпуклых функций, в этом случае последовательность {xk} сходится к точке минимума функции f(x) со скоростью: |xk+n – x*| ≤ C|xk – x*|, k = {0, n, 2, …}
ПРИМЕР. Найти минимум функции методом сопряженных градиентов:
f(X) = 2x12+2x22+2x1x2+20x1+10x2+10.
Решение. В качестве направления поиска выберем вектор градиент в текущей точке:
| ▽ f(X) = |
|
Итерация №0.
| ▽ f(X0) = |
Проверим критерий остановки: |▽f(X0)| < ε
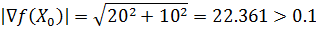 Вычислим значение функции в начальной точке f(X0) = 10.
Вычислим значение функции в начальной точке f(X0) = 10.
Сделаем шаг вдоль направления антиградиента.
| X1 = X0 - t0▽ f(X0) = | - t0 | = |
|
f(X1) = 2*(-20.0*t0)2+2*(-10.0*t0)2+2*(-20.0*t0)*(-10.0*t0)+20*(-20.0*t0)+10*(-10.0*t0)+10 → min
Найдем такой шаг, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f '(x1)=0): 2800*t1-500 = 0
Получим шаг: t0 = 0.1786
|
|
|
Выполнение этого шага приведет в точку:
| X0 = | - 0.1786 | = |
|
Итерация №1.
| ▽ f(X1) = |
|
Проверим критерий остановки:
|▽f(X1)|<ε 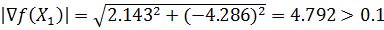
Вычислим значение функции в новой точке f(X1) = -34.643.
X2 = X1 - t1d1
d1 = ▽f(X1) + b0▽f(X0)
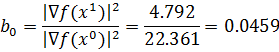
| d1 = |
| + 0.0459 | = |
|
Сделаем шаг вдоль направления антиградиента.
| X2 = X1 - t1▽ f(X1) = |
| - t1 |
| = |
| ||||||||||||
f(X2) = 2*(-3.0612*t1-3.5714)2+2*(3.8265*t1-1.7857)2+2*(-3.0612*t1-3.5714)*(3.8265*t1-1.7857)+20*(-3.0612*t1-3.5714)+10*(3.8265*t1-1.7857)+10 → min
Найдем такой шаг, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f '(x2)=0):
49.198250728863*t2-22.9591836734694 = 0
Получим шаг: t0 = 0.4667
Выполнение этого шага приведет в точку:
| X0 = |
| - 0.4667 |
| = |
|
Итерация №2.
| ▽ f(X2) = |
Проверим критерий остановки: |▽f(X2)| < ε
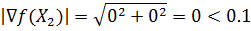 Вычислим значение функции в новой точке f(X2) = -40.
Вычислим значение функции в новой точке f(X2) = -40.
Анализ решения. Найдем матрицу Гессе функции f(X) = 2x12+2x22+2x1x2+20x1+10x2+10.
| H = |
Так как матрица Гессе является положительно определенной, то функция f(X) строго выпукла и, следовательно, в стационарной точке достигает глобальный минимум.
АЛГОРИТМ ДЭВИДОНА - ФЛЕТЧЕРА – ПАУЭЛЛА
Первоначально метод был предложен Дэвидоном и затем развит Флетчером и Пауэллом. Метод Дэвидона-Флетчера-Пауэлла называют также и методом переменной метрики. Он попадает в общий класс квазиньютоновских процедур, в которых направления поиска задаются в виде -Dj*grad(f(y)). Направление градиента является, таким образом, отклоненным в результате умножения на -Dj, где Dj - положительно определенная симметрическая матрица порядка n×n, аппроксимирующая обратную матрицу Гессе. На следующем шаге матрица Dj+1 представляется в виде суммы Dj и двух симметрических матриц ранга один каждая. В связи с этим схема иногда называется схемой коррекции ранга два.
|
|
|
Рассмотрим алгоритм Дэвидона - Флетчера - Пауэлла минимизации дифференцируемой функции нескольких переменных. В частности, если функция квадратичная, то, как будет показано позднее, метод вырабатывает сопряженные направления и останавливается после выполнения одной итерации, т.е. после поиска вдоль каждого из сопряженных направлений.
Начальный этап.
Пусть 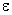 >0 - константа для остановки. Выбрать точку х1 и начальную симметрическую положительно определенную матрицу D1. Положить y1 = x1, k = j = 1 и перейти к основному этапу.
>0 - константа для остановки. Выбрать точку х1 и начальную симметрическую положительно определенную матрицу D1. Положить y1 = x1, k = j = 1 и перейти к основному этапу.
Основной этап.
Шаг 1. Если зк  f(yj) зк< e, то остановиться; в противном случае положить dj = - Dj
f(yj) зк< e, то остановиться; в противном случае положить dj = - Dj  f(yj) и взять в качестве lj оптимальное решение задачи минимизации f(yj + ldj) при l ³ 0. Положить yj+1 = yj + ljdj. Если j < n, то перейти к шагу 2. Если j = n, то положить y1 = xk+1 = yn+1, заменить k на k+1, положить j=1 и повторить шаг 1.
f(yj) и взять в качестве lj оптимальное решение задачи минимизации f(yj + ldj) при l ³ 0. Положить yj+1 = yj + ljdj. Если j < n, то перейти к шагу 2. Если j = n, то положить y1 = xk+1 = yn+1, заменить k на k+1, положить j=1 и повторить шаг 1.
Шаг 2. Построить Dj+1 следующим образом:
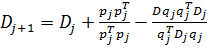 , (1)
, (1)
где pj = ljdj, (2)
qj =  f(yj+1) -
f(yj+1) -  f(yj). (3)
f(yj). (3)
Заменить j на j + 1 и перейти к шагу 1.
Пример. Рассмотрим следующую задачу:
Минимизировать (x1 - 2)4 + (x1 - 2x2)2.
Результаты вычислений методом Дэвидона - Флетчера - Пауэлла приведены в таблице 1.
Таблица 1. Результаты вычислений по методу Дэвидона - Флетчера - Пауэлла.
| k | xk f(xk) | J | yj f(yj) |  f(yj) f(yj)
| зк  f(yj) зк f(yj) зк
| D | dj | lj | yj+1 |
| (0.00, 3.00) (52.00) | (0.00, 3.00) (52.00) (2.70, 1.51) (0.34) | (-44.00, 24.00) (0.73, 1.28) | 50.12 1.47 | 
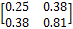
| (44.00, -24.00) (-0.67, -1.31) | 0.062 0.22 | (2.70, 1.51) (2.55, 1.22) | ||
| (2.55, 1.22) (0.1036) | (2.55, 1.22) (0.1036) (2.45, 1.27) (0.0490) | (0.89, -0.44) (0.18, 0.36) | 0.99 0.40 | 

| (-0.89, 0.44) (-0.28, -0.25) | 0.11 0.64 | (2.45, 1.27) (2.27, 1.11) | ||
| (2.27, 1.11) (0.008) | (2.27, 1.11) (0.008) (2.25, 1.13) (0.004) | (0.18, -0.20) (0.04, 0.04) | 0.27 0.06 | 
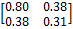
| (-0.18, 0.20) (-0.05, -0.03) | 0.10 2.64 | (2.25, 1.13) (2.12, 1.05) | ||
| (2.12, 1.05) (0.0005) | (2.12, 1.05) (0.0005) (2.115, 1.058) (0.0002) | (0.05, -0.08) (0.004, 0.004) | 0.09 0.006 | 
| (-0.05, 0.08) | 0.10 | (2.115, 1.058) |
На каждой итерации вектор dj для j = 1, 2 определяется в виде
–Dj  f(yj), где D1 – единичная матрица, а D2 вычисляется по формулам (1) - (3). При k = 1 имеем p1 = (2.7, -1.49)T, q1 = (44.73, -22,72)T. На второй итерации p1 = (-0.1, 0.05)T, q1 = (-0.7, 0.8)T и, наконец, на третьей итерации
f(yj), где D1 – единичная матрица, а D2 вычисляется по формулам (1) - (3). При k = 1 имеем p1 = (2.7, -1.49)T, q1 = (44.73, -22,72)T. На второй итерации p1 = (-0.1, 0.05)T, q1 = (-0.7, 0.8)T и, наконец, на третьей итерации
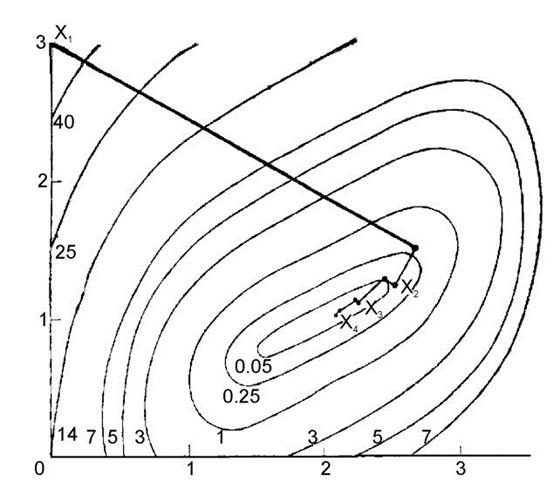
p1 = (-0.02, 0.02)T, q1 = (-0.14, 0.24)T. Точка yj+1 вычисляется оптимизацией вдоль направления dj при начальной точке yj для j = 1, 2. Процедура остановлена в точке y2 = (2.115, 1.058)T на четвертой итерации, так как норма зкf(y2) зк = 0.006 достаточно мала. Траектория движения, полученная методом, показана на рисунке 1.
|
|
|
Рисунок 1. Метод Дэвидона - Флетчера - Пауэлла.
Лемма 1 показывает, что каждая матрица Dj положительно определена и dj является направлением спуска.
Для доказательства леммы нам понадобится:
Теорема 1. Пусть S - непустое множество в Еn, точка x О cl S. Конусом возможных направлений в точке x называется множество D = {d: d ¹ 0, x + ld О S при всех l О (0, d) для некоторого d > 0}.
Определение. Пусть x и y - векторы из Еn и |xTy| - абсолютное значение скалярного произведения xTy. Тогда выполняется следующее неравенство, называемое неравенством Шварца: |xTy| £ ||x|| ||y||.
Лемма 1.
Пусть y1 О Еn, а D1 – начальная положительно определенная симметрическая матрица. Для j = 1,..., n положим
yj+1 = yj + ljdj, где dj = –Dj  f(yj),
f(yj),
а lj является оптимальным решением задачи минимизации f(yj + ldj) при l ³ 0. Пусть, кроме того, для j = 1,..., n – 1 матрица Dj+1 определяется по формулам (1) - (3). Если 
 f(yj) ¹ 0 для j = 1,..., n, то матрицы D1,..., Dn симметрические и положительно определенные, так что d1,..., dn – направления спуска.
f(yj) ¹ 0 для j = 1,..., n, то матрицы D1,..., Dn симметрические и положительно определенные, так что d1,..., dn – направления спуска.
В варианте метода переменной метрики, предложенном Дэвидоном, Флетчером и Пауэллом, для нахождения матрицы 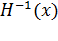 используется матрица
используется матрица 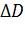 , имеющая ранг, равный 2. Матрица направлений
, имеющая ранг, равный 2. Матрица направлений 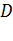 перевычисляется таким образом, чтобы для квадратичной целевой функции после
перевычисляется таким образом, чтобы для квадратичной целевой функции после 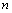 шагов выполнялось
шагов выполнялось  .
.
Исходная матрица 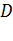 обычно выбирается в виде единичной матрицы
обычно выбирается в виде единичной матрицы 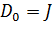 так, что начальное направление минимизации – это направление наискорейшего спуска.
так, что начальное направление минимизации – это направление наискорейшего спуска.
Оценка элементов 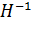 . в точке екстремума
. в точке екстремума  тем точнее, чем лучше мы выберем по сравнению с матрицей
тем точнее, чем лучше мы выберем по сравнению с матрицей 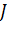 исходную матрицу
исходную матрицу 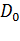 . В процессе оптимизации имеет место постепенный переход от градиентного направления движения к ньютоновскому, при этом используются преимущества каждого из этих методов на соответствующем этапе.
. В процессе оптимизации имеет место постепенный переход от градиентного направления движения к ньютоновскому, при этом используются преимущества каждого из этих методов на соответствующем этапе.
Алгоритм Дэвидона–Флетчера–Пауэлла получим, если в уравнении (6.2.5) положить 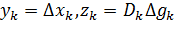 . Тогда
. Тогда
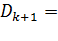
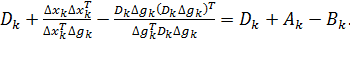 (6.2.10)
(6.2.10)
Заметим, что так как матрицы 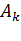 и
и 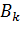 симметричные, то если
симметричные, то если 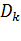 симметричная, то и
симметричная, то и  будет симметричной.
будет симметричной.
|
|
|
Роль матрицы 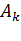 состоит в обеспечении выполнения условия
состоит в обеспечении выполнения условия 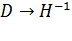 при
при 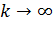 , тогда как
, тогда как 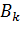 должна обеспечить положительную определенность
должна обеспечить положительную определенность 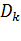 при всех
при всех 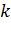 и исключение влияния выбора начальной матрицы D0. Используя (6.2.10) многократно, при условии, что
и исключение влияния выбора начальной матрицы D0. Используя (6.2.10) многократно, при условии, что 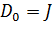 , через
, через 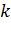 итераций получим
итераций получим
 = J+
= J+ 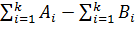
В случае квадратичной функции 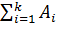 при
при 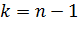 должна равняться
должна равняться 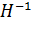 , а
, а 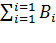 должна быть равна
должна быть равна 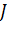 . Заметим, что в случае квадратичной целевой функции в данном алгоритме используются сопряженные направления.
. Заметим, что в случае квадратичной целевой функции в данном алгоритме используются сопряженные направления.
В большинстве вариантов алгоритма функция  минимизируется в каждом выбранном направлении поиска. Для определения минимума
минимизируется в каждом выбранном направлении поиска. Для определения минимума  по
по 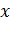 в данном направлении можно применить любую эффективную процедуру одномерного поиска. При этом важно, чтобы эта процедура была эффективной, поскольку значительная часть всего времени вычислений приходится на одномерный поиск.
в данном направлении можно применить любую эффективную процедуру одномерного поиска. При этом важно, чтобы эта процедура была эффективной, поскольку значительная часть всего времени вычислений приходится на одномерный поиск.
 Практика показала, что в некоторых задачах невозможно достичь минимума
Практика показала, что в некоторых задачах невозможно достичь минимума  с помощью методов переменной метрики, если степень точности одномерного поиска недостаточна. Поэтому рекомендуется выбирать точность одномерного поиска по крайней мере эквивалентной точности, требуемой для окончания основного алгоритма.
с помощью методов переменной метрики, если степень точности одномерного поиска недостаточна. Поэтому рекомендуется выбирать точность одномерного поиска по крайней мере эквивалентной точности, требуемой для окончания основного алгоритма.
В качестве критерия останова работы алгоритма авторами было предложено использовать одно из следующих правил.
Каждая из составляющих векторов 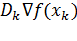 и
и 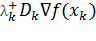 меньше некоторой наперед заданной величины.
меньше некоторой наперед заданной величины.
Вычисленная норма каждого из этих векторов в точке остановки меньше наперед заданной величины.
На рис.6.6 приведена траектория движения по алгоритму Дэвидона–Флетчера–Пауэлла при начальной длине шага 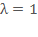 . (Цифры на траектории обозначают номера соответствующих итераций).
. (Цифры на траектории обозначают номера соответствующих итераций).
На практике оказалось, что в данном методе и в других методах переменной метрики могут иногда встречаться шаги в противоположном (относительно направления точки минимума) направлении, либо эти методы могут оканчиваться в нестационарной точке.
Как выяснилось, это является следствием вырождения матрицы 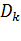 . Если матрица
. Если матрица 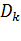 становится почти сингулярной, то направления поиска могут оказаться такими, как при неправильном выборе масштаба по осям координат. Вырождения матрицы
становится почти сингулярной, то направления поиска могут оказаться такими, как при неправильном выборе масштаба по осям координат. Вырождения матрицы 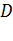 можно избежать либо путем увеличения числа значащих цифр, либо соответствующим выбором масштаба компонент вектора
можно избежать либо путем увеличения числа значащих цифр, либо соответствующим выбором масштаба компонент вектора 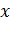 с тем, чтобы сделать порядок диагональных элементов матрицы
с тем, чтобы сделать порядок диагональных элементов матрицы 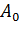 близким к 1.
близким к 1.
Если же эти операции выполнить нельзя, то матрицу 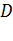 можно перезадать в виде диагональной матрицы, у которой
можно перезадать в виде диагональной матрицы, у которой 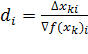 , где
, где  -я компонента вектора
-я компонента вектора 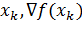 соответственно.
соответственно.
ДОКАЗАТЕЛЬСТВО
Проведем доказательство по индукции. При j = 1 матрица D1 симметрическая и положительно определенная по условию леммы. Кроме того,  f(y1)Td1 = –
f(y1)Td1 = –  f(y1)TD1
f(y1)TD1  f(y1) < 0, так как D1 положительно определена. Тогда по теореме 1 вектор d1 определяет направление спуска. Предположим, что утверждение леммы справедливо для некоторого j £ n – 1, и покажем, что оно справедливо для j+1. Пусть x – ненулевой вектор из En, тогда из (1) имеем
f(y1) < 0, так как D1 положительно определена. Тогда по теореме 1 вектор d1 определяет направление спуска. Предположим, что утверждение леммы справедливо для некоторого j £ n – 1, и покажем, что оно справедливо для j+1. Пусть x – ненулевой вектор из En, тогда из (1) имеем
|
|
|
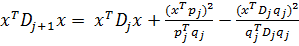 (4)
(4)
Так как Dj – симметрическая положительно определенная матрица, то существует положительно определенная матрица Dj1/2, такая, что Dj = Dj1/2Dj1/2. Пусть a = Dj1/2x и b = Dj1/2qj. Тогда xTDjx = aTa, qjTDjqj = bTb и xTDjqj = aTb. Подставляя эти выражения в (4), получаем:
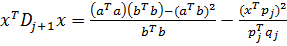 (5)
(5)
По неравенству Шварца имеем (aTa)(bTb) ³ (aTb)2. Таким образом, чтобы доказать, что xTDj+1x ³ 0, достаточно показать, что pjTqj > 0 и bTb > 0. Из (2) и (3) следует, что
pjTqj = ljdjT[  f(yj+1) –
f(yj+1) –  f(yj)]. (6)
f(yj)]. (6)
По предположению  f(yj) ¹ 0, и Dj положительно определена, так что
f(yj) ¹ 0, и Dj положительно определена, так что
 f(yj)TDj
f(yj)TDj  f(yj) > 0. Кроме того, dj – направление спуска, и, следовательно, lj > 0. Тогда из (6) следует, что pjTqj > 0. Кроме того, qj ¹ 0, и, следовательно, bTb= qjTDjqj > 0.
f(yj) > 0. Кроме того, dj – направление спуска, и, следовательно, lj > 0. Тогда из (6) следует, что pjTqj > 0. Кроме того, qj ¹ 0, и, следовательно, bTb= qjTDjqj > 0.
Покажем теперь, что xTDj+1x > 0. Предположим, что xTDj+1x = 0. Это возможно только в том случае, если (aTa)(bTb) = (aTb)2 и pjTx = 0. Прежде всего заметим, что (aTa)(bTb) = (aTb)2 только при a = lb, т.е. Dj1/2x = lDj1/2qj. Таким образом, x = lqj. Так как x ¹ 0, то l ¹ 0. Далее, 0 = pjTx = l pjTqj противоречит тому, что pjTqj > 0 и l ¹ 0. Следовательно, xTDj+1x > 0, т.е. матрица Dj+1 положительно определена.
Поскольку  f(yj+1) ¹ 0 и Dj+1 положительно определена, имеем
f(yj+1) ¹ 0 и Dj+1 положительно определена, имеем
 f(yj+1)Tdj+1 = –
f(yj+1)Tdj+1 = –  f(yj+1)T Dj+1
f(yj+1)T Dj+1  f(yj+1) < 0. Отсюда по теореме 1 следует, что dj+1 – направление спуска.
f(yj+1) < 0. Отсюда по теореме 1 следует, что dj+1 – направление спуска.
Лемма доказана.
Квадратичный случай.
В дальнейшем нам понадобиться:
Теорема 2. Пусть f(x) = cTx + 1 xTHx, где Н - симметрическая матрица порядка n x n. Рассмотрим Н - сопряженные векторы d1, …, dn и произвольную точку x1. Пусть lk для k = 1, …, n - оптимальное решение задачи минимизации f(xk + ldk) при l О Е1 и xk+1 = xk + ldk. Тогда для k = 1, …, n справедливы следующие утверждения:
1.  f(xk+1)Tdj = 0, j = 1, …, k;
f(xk+1)Tdj = 0, j = 1, …, k;
2.  f(x1)Tdk =
f(x1)Tdk =  f(xk)Tdk;
f(xk)Tdk;
3. xk+1 является оптимальным решением задачи минимизации f(x) при условии
x - x1 О L(d1, …, dk), где L(d1, …, dk) – линейное подпространство, натянутое на векторы d1, …, dk, то есть
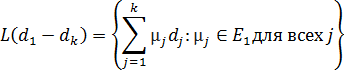
В частности, xn+1 – точка минимума функции f на Еn.
Если целевая функция f квадратичная, то в соответствии со сформулированной ниже теоремой 3 направления d1, …, dn, генерируемые методом Дэвидона - Флетчера - Пауэлла, являются сопряженными. Следовательно, в соответствии с утверждением 3 теоремы 2 метод останавливается после завершения одной итерации в оптимальной точке. Кроме того, матрица Dn+1, полученная в конце итерации, совпадает с обратной к матрице Гессе Н.
Теорема 3. Пусть Н – симметричная положительно определенная матрица порядка n x n. Рассмотрим задачу минимизации f(x) = cTx + 1 xTHx при условии x О En. Предположим, что задача решена методом Дэвидона - Флетчера - Пауэлла при начальной точке y1 и начальной положительно определенной матрице D1. В частности, пусть lj, j = 1, …, n, – оптимальное решение задачи минимизации f(yj + ldj) при l ³ 0 и yj+1 = yj + ljdj, где dj = -Dj  f(yj), а Dj определяется по формулам (1) – (3). Если
f(yj), а Dj определяется по формулам (1) – (3). Если  f(yj) ¹ 0 для всех j, то направления d1, …, dn являются Н - сопряженными и Dn+1 = H-1. Кроме того, yn+1 является оптимальным решением задачи.
f(yj) ¹ 0 для всех j, то направления d1, …, dn являются Н - сопряженными и Dn+1 = H-1. Кроме того, yn+1 является оптимальным решением задачи.
Доказательство.
Прежде всего покажем, что для j, такого, что 1 £ j £ n, справедливы следующие утверждения:
1. d1, …, dj линейно независимы.
2. djTHdk = 0 для i ¹ k; i, k £ j.
3. Dj+1Hpk, или, что эквивалентно, Dj+1Hdk = dk для 1 £ k £ j, pk = lkdk.
Проведем доказательство по индукции. Для j = 1 утверждения 1 и 2 очевидны. Чтобы доказать утверждение 3, заметим прежде всего, что для любого k справедливы равенства
Hpk = H(lkdk) = H(yk+1 - yk) =  f(yk+1) –
f(yk+1) –  f(yk) = qk. (7)
f(yk) = qk. (7)
В частности, Hp1 = q1. Таким образом, полагая j = 1 в (1), получаем
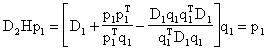 ,
,
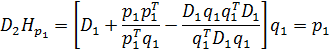
т.е. утверждение 3 справедливо при j = 1.
Теперь предположим, что утверждения 1, 2 и 3 справедливы для j £ n – 1. Покажем, что они также справедливы и для j + 1. Напомним, что по утверждению 1 теоремы 2 diT  f(yj+1) = 0 для i £ j. По индуктивному предположению di = Dj+1Hdi, i £ j. Таким образом, для i £ j имеем
f(yj+1) = 0 для i £ j. По индуктивному предположению di = Dj+1Hdi, i £ j. Таким образом, для i £ j имеем
0 = diT  f(yj+1) = diTHDj+1
f(yj+1) = diTHDj+1  f(yj+1) = –diTHdj+1.
f(yj+1) = –diTHdj+1.
Ввиду предположения индукции это равенство показывает, что утверждение 2 также справедливо для j+1.
Теперь покажем, что утверждение 3 справедливо для j+1.
Полагая k £ j+1, имеем
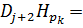
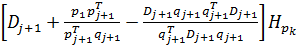 (8)
(8)
Учитывая (7) и полагая k = j + 1 в (8), получим, что Dj+2Hpj+1 = pj+1. Теперь пусть k £ j. Так как утверждение 2 справедливо для j + 1, то
pj+1THpk = lklj+1dj+1THdk = 0. (9)
По предположению индукции из (7) и вследствие того, что утверждение 2 справедливо для j + 1, получаем
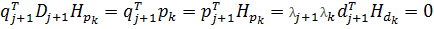 (10)
(10)
Подставляя (9) и (10) в (8) и учитывая предположение индукции, получаем
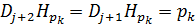
Таким образом, утверждение 3 справедливо для j+1.
Осталось показать, что утверждение 1 справедливо для j+1. Предположим, что 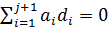 . Умножая это равенство на
. Умножая это равенство на 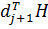 и учитывая, что утверждение 2 справедливо для j+1, получаем, что
и учитывая, что утверждение 2 справедливо для j+1, получаем, что  . По условию теоремы
. По условию теоремы 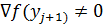 , а по лемме 1 матрица
, а по лемме 1 матрица 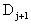 положительно определена, так что
положительно определена, так что 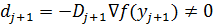 . Так как H положительно определена, то
. Так как H положительно определена, то 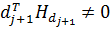 и, следовательно,
и, следовательно, 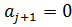 . Отсюда следует, что
. Отсюда следует, что 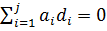 , и так как d1, …, dj линейно независимы по предположению индукции, то
, и так как d1, …, dj линейно независимы по предположению индукции, то 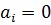 для i = 1, …, j. Таким образом, d1, …, dj+1 линейно независимы и утверждение 1 справедливо для j+1. Следовательно, утверждения 1, 2 и 3 выполняются. В частности сопряжённость d1, …, dn следует из утверждений 1 и 2, если положить j = n.
для i = 1, …, j. Таким образом, d1, …, dj+1 линейно независимы и утверждение 1 справедливо для j+1. Следовательно, утверждения 1, 2 и 3 выполняются. В частности сопряжённость d1, …, dn следует из утверждений 1 и 2, если положить j = n.
Пусть теперь j = n в утверждении 3. Тогда 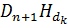 для k = 1, …, n. Если в качестве D взять матрицу, столбцами которой являются векторы d1, …, dn, то
для k = 1, …, n. Если в качестве D взять матрицу, столбцами которой являются векторы d1, …, dn, то 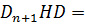 D. Так как D имеет обратную, то
D. Так как D имеет обратную, то 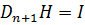 , что возможно только в том случае, если
, что возможно только в том случае, если 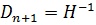 . Наконец,
. Наконец, 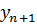 является оптимальным решением по теореме 2.
является оптимальным решением по теореме 2.
Теорема доказана.
МЕТОД КУБИЧЕСКОЙ ИНТЕРПОЛЯЦИИ
Интерполяция – это способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Метод использует кусочную кубическую Эрмитову аппроксимацию и сохраняют монотонность и форму данных. Если какой-либо из элементов вектора xi находится вне интервала, заданного вектором x, то выбранный метод интерполяции используется также и для экстраполяции. Как альтернатива, функция yi = interp1(x, y, xi, method, extrapval) заменяет экстраполированные значения теми, которые заданы вектором extrapval. Для последнего часто используется нечисловое значение NaN. Все методы работают на неравномерной сетке значений вектора x.
При решении реальных задач редко приходится иметь дело с функциями одной переменной. Однако методы одномерной оптимизации важны при многомерной оптимизации, которая выполняется в основном по следующему правилу: зафиксировать некоторую точку, выбрать подходящее направление, выполнить одномерную оптимизацию из выбранной точки в выбранном направлении. Поэтому методы интерполяции полезны для выполнения линейного поиска при оптимизации функций многих переменных. В этом случае обычно требуется найти минимум функции 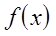 в точках прямой
в точках прямой 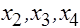 , где
, где 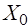 - заданная точка,
- заданная точка, 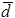 - определенное направление. Значение функции
- определенное направление. Значение функции 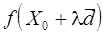 на этой прямой являются значениями функции одной переменной l:
на этой прямой являются значениями функции одной переменной l: 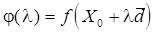 .
.
Рассмотрим метод Дэвидона, в котором функция аппроксимируется кубическим полиномом, и который обеспечивает большую точность определения точки минимума. Обсуждение метода проведем в виде, пригодном для многомерной оптимизации.
Для интерполяции используются значения функции и ее производной, вычисленные в двух точках.
Пусть минимизируется функция 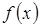 на прямой
на прямой 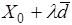 , то есть функция
, то есть функция

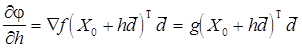 .
.
Предполагаем, что известны следующие значения:
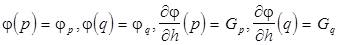 .
.
Эту информацию можно использовать для построения кубического полинома 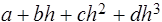 , который и будет аппроксимировать функцию j(h).
, который и будет аппроксимировать функцию j(h).
Если выбрать p=0 (для простоты), то уравнения, определяющие a, b, c, d, выглядят так:
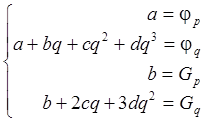
Эти уравнения имеют решение:
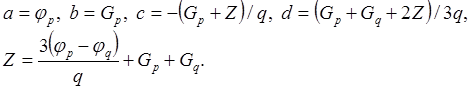
Стационарные точки кубического полинома являются решением уравнения
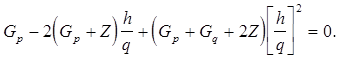
Точкой минимума кубического полинома является
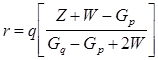 ,
, 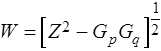 (*)
(*)
Как уже отмечалось, это все выполняется при 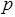 =0. Выбор q осуществляется из следующих соображений.
=0. Выбор q осуществляется из следующих соображений.
Если 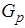 < 0, то следует выбирать q>0, то есть сделать шаг в направлении убывания функции j(h). В противном случае q<0. Значение q должно быть таким, чтобы интервал (0, q) содержал минимум. Это будет верно, если j(q)>j(p) или
< 0, то следует выбирать q>0, то есть сделать шаг в направлении убывания функции j(h). В противном случае q<0. Значение q должно быть таким, чтобы интервал (0, q) содержал минимум. Это будет верно, если j(q)>j(p) или 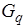 >0 (даже при j(q)<j(p)). Если ни одно из этих условий не выполнено, то надо удвоить q, повторяя это до тех пор, пока полученный интервал не будет содержать минимум.
>0 (даже при j(q)<j(p)). Если ни одно из этих условий не выполнено, то надо удвоить q, повторяя это до тех пор, пока полученный интервал не будет содержать минимум.
Остается задача определения начальной величины q. Значение q, которое было бы одинаково приемлемо для всех задач, выбрать весьма сложно. Дэвидон, Флетчер и Пауэлл предложили выбирать q следующим образом:
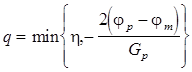 , где
, где 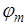 - оценка наименьшего значения j(h), h = const (2 или 1).
- оценка наименьшего значения j(h), h = const (2 или 1).
Алгоритм кубической интерполяции.
1. Найти 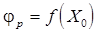 и
и 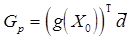 .
.
2. Проверить, выполняется ли условие 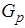 <0. Если не выполняется, производить поиск в направлении -
<0. Если не выполняется, производить поиск в направлении - 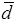 , иначе - в направлении
, иначе - в направлении 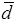 . Выбрать q в соответствии с рекомендациями (при этом необходимо "угадать"
. Выбрать q в соответствии с рекомендациями (при этом необходимо "угадать" 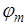 ).
).
3. Вычислить 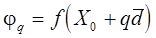
4. Если 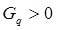 или
или 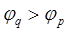 , то интервал, содержащий минимум, найден. Иначе положить q = 2q и перейти к 3.
, то интервал, содержащий минимум, найден. Иначе положить q = 2q и перейти к 3.
5. Использовать выражение (*) для аппроксимации точки минимума на интервале (0, q) значением r.
6. Если 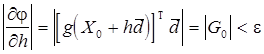 , где e - заданная точность, то остановиться.
, где e - заданная точность, то остановиться.
7. Вернуться на шаг 5, используя интервал (0, r), если 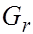 >0, либо используя интервал (r, q), если
>0, либо используя интервал (r, q), если 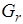 < 0.
< 0.
Рассмотренный метод кубической интерполяции является одним из интерполяционных методов Эрмита, приспособленным специально для оптимизации. Этот метод требует знания производных функций и используется в основном в так называемых квазиньютоновских методах многомерной оптимизации, которые и сами по себе используют производные.
ЗАКЛЮЧЕНИЕ
Метод сопряженных градиентов формирует направления поиска, в большей мере соответствующие геометрии минимизируемой функции.
Первоначально метод был предложен Дэвидоном и затем развит Флетчером и Пауэллом. Метод Дэвидона-Флетчера-Пауэлла называют также и методом переменной метрики. Он попадает в общий класс квазиньютоновских процедур, в которых направления поиска задаются в виде -Dj*grad(f(y)). Направление градиента является, таким образом, отклоненным в результате умножения на -Dj, где Dj - положительно определенная симметрическая матрица порядка n×n, аппроксимирующая обратную матрицу Гессе. На следующем шаге матрица Dj+1 представляется в виде суммы Dj и двух симметрических матриц ранга один каждая. В связи с этим схема иногда называется схемой коррекции ранга два.
Интерполяция – это способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Метод использует кусочную кубическую Эрмитову аппроксимацию и сохраняют монотонность и форму данных.
При решении реальных задач редко приходится иметь дело с функциями одной переменной. Однако методы одномерной оптимизации важны при многомерной оптимизации, которая выполняется в основном по следующему правилу: зафиксировать некоторую точку, выбрать подходящее направление, выполнить одномерную оптимизацию из выбранной точки в выбранном направлении. Поэтому методы интерполяции полезны для выполнения линейного поиска при оптимизации функций многих переменных.
СПИСОК ЛИТЕРАТУРЫ
1. Кононюк А.Е. Основы теории оптимизации, 2011
Летова Т. А., Пантелеев А. В. Методы оптимизации. Практический курс, 2011
3. Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах, 2005
|
|
|


