 |
Проецирование центральное
|
|
|
|
Лекция 1 Предмет начертательной геометрии. Виды проецирования. Метод Монжа.
Начертательная геометрия является наивысшим средством развития той
таинственной способности человеческого духа, которая зовется воображением и которая является ступенью к другой царственной способности – фантазии, без которой почти не совершаются великие открытия и изобретения
Н.А. Рынин
В основе правил построения изображений, рассматриваемых в начертательной геометрии и применяемых в черчении, лежит метод проекций. Изучение начинается с построения проекций точки, так как при построении изображений любой пространственной формы рассматривается ряд точек, принадлежащих этой форме.
В настоящем учебном пособии приняты следующие буквенно-цифровые обозначения геометрических фигур.
Геометрические образы
1. Плоскость проекций:
p – произвольная;
p1 – горизонтальная;
p2 – фронтальная;
p3 – профильная;
S – центр проецирования.
2. Оси проекции:
X – ось абсцисс;
Y – ось ординат;
Z – ось аппликат;
Начало координат – прописной буквой О.
1. Точки, расположенные в пространстве, обозначаются прописными буквами латинского алфавита, а также арабскими цифрами:
A, B, C, D,…, L, M, N,
1, 2, 3, 4,…,12, 13, 14,…
2. Линии, расположенные произвольно относительно плоскостей проекций, обозначаются строчными буквами латинского алфавита:
a, b, c,…, l, m, n
Линии уровня обозначаются:
h – горизонталь;
f – фронталь;
p – профильная прямая.
Для прямых линий используются также следующие обозначения:
(A, B) – прямая, проходящая через точки A и B;
[AB] – отрезок прямой, ограниченный точками А и В
3. Плоскости обозначаются прописными буквами латинского и греческого алфавита:
|
|
|
P, Q, R, S, T, S, L, Q …
Для обозначения плоскостей уровня используются прописные буквы только греческого алфавита:
Г – горизонтальная плоскость (гамма);
Ф – фронтальная плоскость (фи);
Р – профильная плоскость (ро).
Чтобы выделить способ задания плоскости, указывают ее геометрические элементы, которыми она определяется:
P (D ABC) – плоскость P задана треугольником ABC;
Q (a 
b) – плоскость Q задана пересекающимися прямыми a и b;
R (m II n) – плоскость R задана параллельными прямыми m и n;
S (A,В,С) – плоскость S задана тремя точками.
4. Проекции точек, линий и других геометрических образов обозначаются теми же буквами (или цифрами), что и оригинал, но с добавлением индекса А1, А2, А3 или 11, 12, 13, соответствующего плоскости проекций, на которой они получены:
А1, В1, С1, …, М1, N1… – горизонтальные проекции точек;
А2, В2, С2, …, М2, N2… – фронтальные проекции точек;
А3, В3, С3, …, М3, N3… – профильные проекции точек;
a1, b1, c1, …, m1,n1… – горизонтальные проекции линий;
a2, b2, c2, …, m2,n2… – фронтальные проекции линий;
a3, b3, c3,…, m3,n3… – профильные проекции линий и т. д.
Обозначение отношений между геометрическими образами
Обозначения теоретико-множественные
Сущность метода проецирования заключается в том, что проекция Аp некоторого геометрического образа А получается в результате пересечения проецирующей линии n, проходящей через точку А с плоскостью проекций p (рис.1.1):
Рис. 1.1
p – плоскость проекций;
А – геометрический образ пространства;
n – проецирующая линия;
Аp = n p I А – проекция геометрического образа пространства на плоскость проекций.
Для получения проекции линии проецируют ряд ее точек с последующим соединением полученных проекций точек (рис. 1.2).
Знание построения проекций точек и линий позволяет перейти к проецированию поверхности тела.
Рис. 1.2
Способ проецирования
В начертательной геометрии рассматриваются два основных способа проецирования: центральное и параллельное.
|
|
|
Проецирование центральное
Центральным называется проецирование, при котором все проецирующие лучи выходят из одной точки S, называемой центром проецирования. На рис. 1.3 дан пример центрального проецирования, где p – плоскость проекций; S – центр проецирования (точка, не лежащая в плоскости p); А, В, С – точки пространства; Аp, Вp, Сp – центральные проекции точек А, В, С, на плоскость p: они получаются в пересечении проецирующих лучей SA, SB, SC c плоскостью проекций.
Если для некоторой точки D проецирующий луч окажется параллельным плоскости проекций, то принято считать, что они пересекаются, но в бесконечно удаленной точке. Проекцией точки D будет бесконечно удаленная точка Dp.
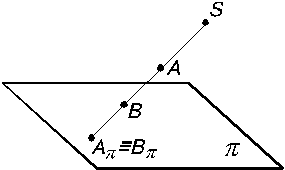
Проекции точек (А и В), лежащих на одном проецирующем луче, совпадают (Аp 
Вp) (рис. 1.4).
| 
|
| Рис. 1.3 | Рис. 1.4 |
Построение центральных проекций прямой линии АВ и кривой MN показано на (рис. 1.5 и 1.6).
| 
|
| Рис. 1.5 | Рис. 1.6 |
|
|
|
