 |
Методы отсечения. Метод Гомори
|
|
|
|
Лекция № 4 «ЦЕЛОЧИСЛЕННОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ»
Постановка задачи целочисленного программирования
По смыслу значительной части экономических задач, относящихся к задачам линейного программирования, компоненты решения должны выражаться в целых числах, т.е. быть целочисленными. К ним относятся, например, задачи, в которых переменные означают количество единиц неделимой продукции, число станков при загрузке оборудования, число судов при распределениях по линиям, число турбин в энергосистеме, число вычислительных машин в управляющем комплексе и многие другие.
Задача линейного целочисленного программирования формулируется следующим образом: найти такое решение (план) х = (х1, х2,…, хn), при котором линейная функция
 (4.1)
(4.1)
принимает максимальное или минимальное значение при ограничениях
 (4.2)
(4.2)
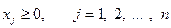 (4.3)
(4.3)
 (4.4)
(4.4)
Следует отметить, что классическая транспортная задача и некоторые другие задачи транспортного типа «автоматически» обеспечивают решение задачи в целых числах (если, конечно, целочисленны параметры условий). Однако в общем случае условие целочисленности (4.4), добавляемое к обычным задачам линейного программирования, существенно усложняет ее решение.
Для решения задач линейного целочисленного программирования используется ряд методов. Самый простой из них - обычный метод линейного программирования. В случае если компоненты оптимального решения оказываются нецелочисленными, их округляют до ближайших целых чисел. Этот метод применяют тогда, когда отдельная единица совокупности составляет малую часть объема всей совокупности. В противном случае округление может привести к далекому от оптимального целочисленному решению, поэтому используют специально разработанные методы.
|
|
|
Методы целочисленной оптимизации можно разделить на три основные группы:
Þ методы отсечения;
Þ комбинаторные методы;
Þ приближенные методы.
Остановимся подробнее на методах отсечения.
Методы отсечения. Метод Гомори
Сущность методов отсечения состоит в том, что сначала задача решается без условия целочисленности. Если полученный план целочисленный, задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:
Ø оно должно быть линейным;
Ø должно отсекать найденный оптимальный нецелочисленный план;
Ø не должно отсекать ни одного целочисленного плана.
Дополнительное ограничение, обладающее указанными свойствами, называется правильным отсечением.
Далее задача решается с учетом нового ограничения. После этого в случае необходимости добавляется еще одно ограничение и т. д.
Если наложить требование целочисленности, то допустимое множество решений вырождается в систему точек и уже в общем случае не является выпуклым. Если добавить новые ограничения, связывающие внешние целочисленные точки,
 а затем в качестве многоугольника (многогранника) решений использовать все выпуклое множество, то получим новую задачу линейного программирования со следующими свойствами:
а затем в качестве многоугольника (многогранника) решений использовать все выпуклое множество, то получим новую задачу линейного программирования со следующими свойствами:
Рис. 4.1
Ø новый многоугольник решений содержит все целые точки, заключавшиеся в первоначальном многоугольнике (многограннике) решений; любая угловая его точка является целой;
Ø так как линейная функция достигает оптимума в угловой точке многоугольника (многогранника) решений, то построением такого многоугольника и обеспечивается целочисленность оптимального решения.
Решение поставленной задачи ведем симплексным методом без учета требования целочисленности. Если оптимальный план целочисленный, то вычисления заканчивают; если же в оптимальном решении такой задачи хотя бы одна компонента не будет целым числом, то вводятся дополнительные ограничения и процесс решения продолжается.
|
|
|
Предположим, что, максимизируя (4.1) при условиях (4.2) и (4.3) без учета требования целочисленности переменных, мы пришли к оптимальному решению с предпочитаемым эквивалентом системы ограничений (4.2) вида:
 (а)
(а)
Пусть правые части fj некоторых уравнений оказались дробными. Выберем одну из них, например f1. Каждый коэффициент e1j при неизвестной в соответствующем уравнении системы и свободный член f1 представим в виде суммы целой части и правильной неотрицательной дроби
 (4.5)
(4.5)
помня, что целой частью любого числа называется наибольшее целое число, не превосходящее данного числа. Тогда соответствующее уравнение системы можно записать:

или (b)

где k=n+m
Левая часть этого равенства должна быть числом целым, так как мы требуем, чтобы все переменные принимали целые неотрицательные значения. Поэтому и правая часть должна быть целым числом и, очевидно, это число не больше, чем γ1. Но γ1 есть правильная не отрицательная дробь и, следовательно, правая часть не может превышать нуля:
 (c)
(c)
откуда
 (d)
(d)
Вычитая из левой части новую неотрицательную неизвестную xn + l заменим неравенство (d) уравнением:

или
 (4.6)
(4.6)
где γ1,m+1, γ1,m+2, …, - коэффициенты, стоящие в первой строке оптимальной, но нецелочисленной таблицы, и под неизвестными xm + l, xm + 2,….
Это и есть дополнительное ограничение, которое следует ввести. Новая задача с (m + 1) уравнениями (4.2) и (4.6) является задачей дискретного программирования, так как «-хn + 1» совпадает с правой частью равенства (b). На данном этапе значение хn + 1 равно «- γ1» т. е. отрицательно и дробно. Мы добавляем к последней симплексной таблице еще одну строку, соответствующую уравнению (4.6). При этом относительные оценочные коэффициенты не изменяются, т. е. условие оптимальности сохраняется.
Возобновляя процесс преобразования симплексных таблиц, применим двойственный метод и переведем неизвестную хn + 1 из базисных в свободную. Возможно, что после этого получится базисное неотрицательное решение с целочисленными компонентами и задача решена. Если нет, то составляем следующее дополнительное ограничение, учитывающее целочисленность. Процесс присоединения дополнительных ограничений повторяют до тех пор, пока либо будет найден целочисленный оптимальный план, либо будет доказано, что задача не имеет целочисленных планов.
|
|
|
Если имеются несколько дробных fi то дополнительное ограничение (4.6) составляют для mахγ1. Это ускоряет процесс получения оптимального целочисленного решения.
4.3. Задача определения оптимального плана производства
Пусть предприятие для производства трех размерных наименований изделий использует три вида ресурсов в количестве 10, 11 и 13 ед. Затраты каждого из перечисленных трех видов ресурсов на изготовление одного изделия 1-го, 2-го или 3-го видов и прибыль от реализации одного изделия каждого из видов отражены в табл. 4.1.
Таблица 4.1
| Объем ресурсов | Затраты на одно изделие | ||
| l-го вида | 2- го вида | 3-го вида | |
| Прибыль в усл. ед. |
Предполагая, что предприятие может выпускать изделия разных наименований в любых соотношениях, найти план производства, обеспечивающий максимальную рентабельность.
Если обозначить через хl, х2 и х3 ед. количество изделий, которые должно выпускать предприятие для обеспечения максимальной рентабельности, то имеем задачу целочисленного программирования.
Максимизировать линейную функцию
 (e)
(e)
при ограничениях
 (f)
(f)
Соответственно соотношениям (e) и (f) записываем систему уравнений:
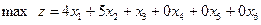
 (g)
(g)
Строим симплексную таблицу 4.2. Произведя три шага симплексных преобразований, получаем табл. 4.3 – 4.5.
Таблица 4.2
| № 1 | cj | c0 | ||||
| ci | СП БП | ai0 | х1 | х2 | х3 | aio/aij* |
| х4 | ||||||
| х5 | 
| |||||
| х6 | 
| |||||
| - | z=Δ | -4 | -5 | -1 | - |
Таблица 4.3
| № 2 | cj | c0 | ||||
| ci | СП БП | ai0 | х1 | х5 | х3 | aio/aij* |
| х4 | 
| 
| 
| 
| ||
| х2 | 
| 
| 
| |||
| х6 | 
| 
| 
| 
| ||
| - | z=Δ | 
| 
| 
| -1 | - |
Таблица 4.4
|
|
|
| № 3 | cj | c0 | ||||
| ci | СП БП | ai0 | х4 | х5 | х3 | aio/aij* |
| х1 | 
| 
| 
| |||
| х2 | 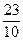
| 
| 
| |||
| х6 | 
| 
| 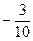
| 
| ||
| - | z=Δ | 
| 
| 
| -1 | - |
Таблица 4.5
| № 4 | cj | c0 | ||||
| ci | СП БП | ai0 | х4 | х5 | х6 | aio/aij* |
| х1 | 
| 
| 
| - | ||
| х2 | 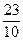
| 
| 
| - | ||
| х3 | 
| 
| 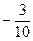
| - | ||
| - | z=Δ | 
| 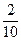
| 
| - |
Табл. 4.5 дает оптимальное, но нецелочисленное решение
х =( ,
, 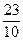 ,
,  , 0, 0, 0) и max z(x) =
, 0, 0, 0) и max z(x) = 
Для отыскания целочисленного решения нужно ввести дополнительное ограничение (4.6).
Из соотношений (4.5):

Так как mах γ i = mах ( ), тогда дополнительное ограничение (4.6) строим для х1 -строки табл. 4.5.
), тогда дополнительное ограничение (4.6) строим для х1 -строки табл. 4.5.
Находим

Тогда γ11=γ14, γ12=γ15, γ13=γ16 и дополнительное ограничение имеет вид:
-γ14 х4 - γ15 х5 - γ16 х6 + х7 = - γ1 или
 (h)
(h)
Вводя уравнение (h) как новую строку в табл. 4.5, получим табл. 4.6 и, совершая симплексное преобразование с разрешающим элементом «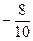 » (освобождаемся от отрицательного элемента в 1-столбце), придем к табл. 4.7.
» (освобождаемся от отрицательного элемента в 1-столбце), придем к табл. 4.7.
Таблица 4.6
| № 5 | cj | c0 | ||||
| ci | СП БП | ai0 | х4 | х5 | х6 | aio/aij* |
| х1 | 
| 
| 
| - | ||
| х2 | 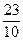
| 
| 
| - | ||
| х3 | 
| 
| 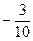
| - | ||
| х7 | 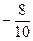
| 
| 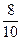
| - | ||
| - | z=Δ | 
| 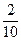
| 
| - |
Таблица 4.7
| № 6 | cj | c0 | ||||
| ci | СП БП | ai0 | х4 | х7 | х6 | aio/aij* |
| х1 | 
| 
| 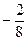
| - | ||
| х2 | 
| 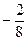
| 
| - | ||
| х3 | 
| 
| 
| - | ||
| х5 | 
| 
| 
| - | ||
| - | z=Δ | 
| 
| 
| - |
Из табл. 4.7 получаем оптимальное целочисленное решение хопт =(2; 2; 1; 0; 1; 0; 0) и max z = 19.
Следовательно, максимальная прибыль в 19 усл. ед. будет достигнута при производстве двух ед. изделий l-го вида, двух ед. изделий 2-го вида и одной ед. изделий 3-го вида.
|
|
|


