Измерение функций распределения вероятностей

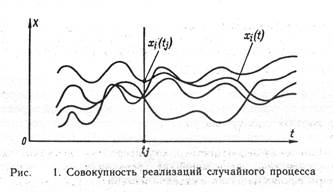
Одномерная интегральная функция распределения вероятно­сти F (X) равна вероятности того, что мгновенное значение про­извольной реализации в произвольный момент времени меньше установленного уровня, т. е. X i (t i) £ X. Функция F (X) определя­ется как предел выборочного среднего:

 

F (X)= lim S d [j [ x (t),X]],

      d ®¥       

 

                      1 при x (t) £ X

Где j[ x (t),X]=

                      0 при x (t) > X

 

Поскольку интегральные F (X) и дифференциальные w (X) функции распределения вероятности связаны между собой со­отношениями

                                                      X

w (X) =(dF (X))/ dX; F (X)= ò w (X) dX

                                      -¥

справедливо выражение

w (X) = lim ((F(X+ DX)-F (X))/ DX)= lim ((S d [Dj[ x (t),X]])/ DX)

       DX®0                                             DX®0   

 

                      1 при X < x (t) £ X+ DX

где Dj [ x (t),X]=

                      0 при x (t) £ X, x (t) > X+ DX

 

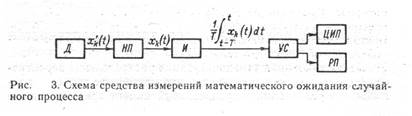
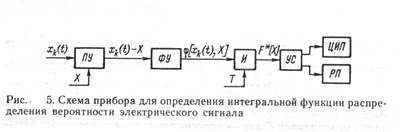
В качестве примера рассмотрим средство измерений для определения интегральной функции распределения вероятности уровня электрического сигнала. Схема средства измерений, реа­лизующего алгоритм

              t                          

F * (X)= 1/T ò j [ x k (t),X] dt,

            t-T                        

 

показана на рис. 5, где ПУ — пороговое устройство, формиру­ющее сигнал X k (t }—X; ФУ— формирующее устройство; И— интегратор, на выходе которого получается сигнал F* (X) при установленных значениях Х и Т; УС — устройство сопряжения;

ЦИП — цифровой прибор; РП — регистрирующий прибор.

Средняя квадратическая погрешность из-за конечности объема выборки определяется для F {X) с помощью соотношения

 

            2        1/2

s =[2(F - F) t k /T]

      F°

 

при усреднении по времени и с помощью соотношения

                  2  1/2

s =[2(F - F)/N]

      F°

при усреднении по совокупно­сти. Для (X) соответствующие соотношения имеют вид:

              2             1/2

s =[2(w - w  DX) t k /T]

      w °

 

              2         1/2

и s =[(w - w  DX)/N]

        w °

 

В приведенных соотношениях F и w — истинные значения измеряемых функ­ций при данном X.

 

ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННОЙ ФУНКЦИИ

Для случайного процесса с нулевым математическим ожида­нием корреляционная функция равна:

R x (s, t) = lim S d [ x i (t) x i - s (t - t)],

               d ®¥

где t и s — соответственно сдвиг во времени и в пространстве реализации перемножаемых мгновенных значений.  

В практических задачах большую роль играют стационарные случайные процессы, т. е. процессы с постоянными вероятностны­ми характеристиками, не зависящими от текущего времени. Сре­ди случайных процессов можно выделить эргодические процессы, для которых

                     t

R x (t) = lim 1/T ò x (t) x (t -t) dt,

           T ®¥           0

 

Большое значение корреляционного анализа в различных областях науки и техники привело к созданию множества измери­тельных приборов для измерений корреляционных функций — коррелометров.

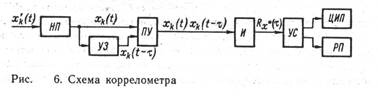
Типовая структура коррелометра, в котором используется усреднение по времени, представлена на рис. 6. При этом реализуется следующий алгоритм:

                t

R* x (t) = 1/T ò x k (t) x k (t -t) dt,

                      t - T

 

Как видно, после нормирующего преобразователя НП сигнал поступает в устройство временной задержки УЗ и на перемножа­ющее устройство ПУ, осуществляющее перемножение мгновен­ных значений, сдвинутых по времени на интервал т. Далее с по­мощью интегратора И выполняется усреднение, после которого результирующий сигнал через УС подается на цифровой прибор ЦИП или регистрирующий прибор РП.

Средние квадратические погрешности, обусловленные ко­нечностью объема выборочных данных о мгновенных значениях реализации процесса Х (t), оцениваются с помощью соотноше­ний:

 

                                           1/2

s ={2D[ x k (t) x k (t-t)] t k /T}

          R°

 

 при усреднении по времени Т и

                                    1/2

s ={D[ x k (t) x k (t-t)]/N}

          R°

 

при усреднении по совокупности.

АНАЛИЗ СПЕКТРА МОЩНОСТИ

Спектр мощности характеризует ее частотное распределение, и он может быть определен в соответствии со следующими форму­лами: 

                                    2

S x (w) = lim 1/T | x iT (w) |

             T ®¥

Где

              t         -jwt’    

XiT (w) = ò xi (t’) e  dt’

            t-T

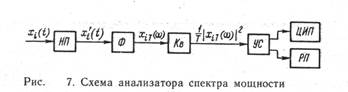
На рис. 7 изображена схема анализатора спектра мощно­сти случайного процесса Х (t).

С выхода нормирующего преобразователя НП i -я реализация случайного процесса x i (t) поступает на блок Ф, выполняющий преобразование Фурье, после чего узлом Кв производится возве­дение в квадрат и нормирование с учетом интервала усреднения Т. С помощью устройства сопряжения УС сформированный сиг­нал поступает на ЦИП и регистратор РП.

В настоящее время отечественной промышленностью серийно выпускаются анализаторы случайных процессов. К ним относят­ся многофункциональный статистический преобразователь Ф790, корреллометр Ф7016, комплекс измерителей характеристик случайных сигналов Х6-4/а, многофункциональные измерители ве­роятностных характеристик Ф36 и Ф37, анализаторы спектра Ф4326, Ф4327, Ф7058 и др. С помощью этих приборов и устройств можно измерять математические ожидания и дисперсии, а также значения функций распределения вероятности, корреляционных и спектральных функций с последующим восстановлением вида самих функций. Перечисленные анализаторы рассчитаны в ос­новном на унифицированный входной сигнал и позволяют изме­рить от 256 до 4096 ординат анализируемой функции. Погреш­ность измерения не превышает ±5 %.

Кроме того, для определения вероятностных характеристик случайных сигналов могут использоваться электроизмеритель­ные приборы, предназначенные для измерения среднего и дей­ствующего значений сигнала. Для определения среднего значе­ния применяют магнитоэлектрические приборы и цифровые ин­тегрирующие приборы. Для определения среднего квадратического отклонения используют приборы, показания которых определяются действующим значением сигнала (термоэлектри­ческие, электростатические и др.).

Корреляционные устройства получили применение в различ­ных областях науки и техники для измерения различных величин. В качестве примера можно указать корреляционное устройство для измерения скорости прокатки. Эти устройства измеряют кор­реляционную функцию, зависящую от т, которая, в свою очередь, зависит от скорости прокатки.

 

Список литературы:

1.Метрология и электроизмерительные приборы. Душин М.Е.\М.: Энергоатомиздат,1986.

 

2.Метрология, стандартизация и измерения в технике связи. Под ред. Б.П. Хромого

М.: Радио и связь, 1986.

 

3.Основы метрологии и стандартизации. Голубева В. П. \М.: Вектор, 1996. 

 

12	Поделиться:

Воспользуйтесь поиском по сайту: